Уравнения – это один из основных разделов математики, с которым сталкиваются ученики в школе. Выполняя уравнения, ученики учатся решать математические задачи, развивая навыки логического мышления. Однако иногда можно столкнуться с двумя разными уравнениями, и встает вопрос: равносильны ли они?
Равносильность уравнений означает, что они имеют одинаковое решение. То есть, если оба уравнения имеют один и тот же набор значений переменных, то они равносильны. Для того чтобы проверить равносильность уравнений, нужно выполнить ряд шагов, которые помогут определить их эквивалентность.
Методы сравнения уравнений

Использование эквивалентных преобразований
Для проверки равносильности уравнений в 10 классе можно использовать эквивалентные преобразования. Эти преобразования позволяют изменять уравнение так, чтобы оно выглядело по-другому, но при этом не изменяло своего смысла.
Одним из основных методов эквивалентных преобразований является добавление или вычитание одного и того же числа или многочлена к обеим сторонам уравнения. Это позволяет упростить уравнение и проверить его равносильность.
Другим методом является умножение или деление обеих сторон уравнения на одно и то же число или многочлен. Это также помогает упростить уравнение и проверить его равносильность.
Используя эквивалентные преобразования, можно убедиться в том, что два уравнения равносильны, то есть имеют одни и те же корни, решения или значения переменных.
Подстановка различных значений переменных

Для проверки равносильности уравнений в 10 классе можно использовать метод подстановки различных значений переменных. Для этого выберите некоторые значения переменных, подставьте их в уравнение и вычислите результат. Затем подставьте эти же значения в другое уравнение и сравните результаты. Если значения в обоих случаях одинаковы, то уравнения равносильны.
Например, если даны уравнения: x + 2 = 5 и 3x = 6, то можно подставить x = 3. Подставив это значение в первое уравнение, получим 3 + 2 = 5, что верно. Затем подставив x = 3 во второе уравнение, получим 3*3 = 6, что также верно. Следовательно, уравнения равносильны.
Критерии равносильности уравнений

Для того чтобы проверить, равносильны ли уравнения в 10 классе, следует руководствоваться определенными критериями:
1. Определить, содержат ли оба уравнения одинаковые переменные и коэффициенты при них. В случае, если все переменные и коэффициенты равны, уравнения равносильны.
2. Проверить, имеют ли оба уравнения одинаковое решение. Если решение одного уравнения является решением другого, то уравнения равносильны.
3. Преобразовать уравнения к эквивалентным формам с помощью допустимых математических операций (сложение, вычитание, умножение, деление), при этом сохраняя равенство. Если полученные уравнения идентичны, то исходные уравнения равносильны.
4. Использовать метод проверки путем подстановки решения одного уравнения в другое. Если при подстановке решения первого уравнения во второе обе части равенства совпадают, то уравнения равносильны.
Определение одинаковых корней

Для определения того, равносильны ли уравнения, необходимо рассмотреть их корни. Два уравнения будут иметь одинаковые корни, если их корни совпадают.
Для нахождения корней уравнения можно воспользоваться формулой для решения квадратного уравнения: x = (-b ± √(b² - 4ac)) / 2a, где a, b, c - коэффициенты уравнения ax² + bx + c = 0.
Вычислив корни обоих уравнений и сравнив их, можно определить, равносильны ли уравнения. Если корни совпадают, то уравнения равносильны, если нет - они различны.
| Уравнение 1 | Уравнение 2 | Одинаковые корни |
|---|---|---|
| ax² + bx + c = 0 | px² + qx + r = 0 | Корни x1, x2 |
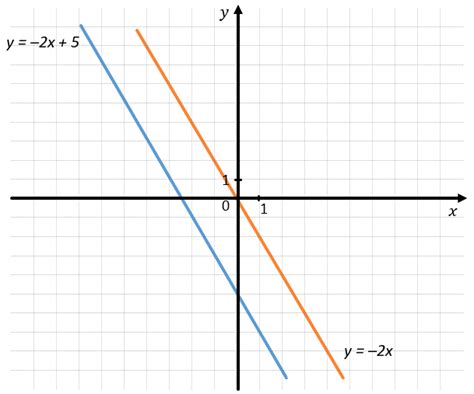
Совпадение графиков функций
Вопрос-ответ

Как проверить, равносильны ли уравнения в 10 классе?
Для проверки равносильности двух уравнений в 10 классе необходимо сравнить их решения: если при любых допустимых значениях переменных обе стороны уравнений равны между собой, то уравнения равносильны. Это можно продемонстрировать, проведя подробное аналитическое сравнение решений, либо выполнив несколько примеров с числовыми значениями переменных.
Какой метод можно использовать для определения равносильности уравнений?
Один из методов для определения равносильности уравнений - это приведение обоих уравнений к одинаковому виду, например, к канонической форме или к виду, удобному для сравнения. Затем проводится анализ коэффициентов, степеней переменных и других параметров уравнений для сравнения их структуры. При выполнении этой процедуры важно учитывать все возможные случаи и варианты, чтобы быть уверенным в равносильности уравнений.



