Треугольник – одна из основных геометрических фигур, состоящая из трех отрезков – сторон и трех углов. Интересно, можно ли определить длины сторон треугольника, зная только его углы? Вопрос этот волнует многих, кто интересуется геометрией и решением геометрических задач.
Как найти стороны треугольника
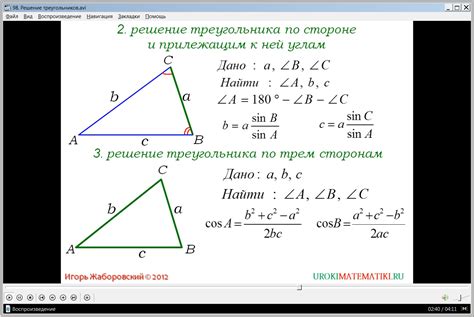
Для нахождения сторон треугольника по известным углам можно воспользоваться тригонометрическими функциями. При известных углах треугольника (назовем их α, β, γ) можно применить правило синусов: отношение стороны к синусу противоположного угла одинаково для всех сторон.
Формула для применения правила синусов:
- a/sin(α) = b/sin(β) = c/sin(γ)
Где a, b, c - стороны треугольника, α, β, γ - соответствующие углы. Из этой формулы можно выразить каждую сторону в зависимости от синуса соответствующего угла.
Таким образом, зная углы треугольника, можно вычислить длины его сторон с помощью правила синусов.
Математические методы и формулы
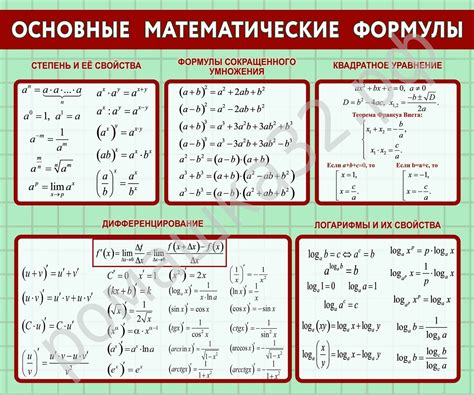
Для нахождения сторон треугольника по известным углам можно использовать формулу синусов:
1. Формула синусов: Для любого треугольника ABC с углами A, B и C и сторонами a, b и c соответственно, справедливо:
a/sin(A) = b/sin(B) = c/sin(C)
Эта формула позволяет найти стороны треугольника, если известны углы и одна сторона. Или наоборот, если известны стороны и один угол, можно найти другие стороны и углы.
Сумма углов и площадь

В треугольнике сумма всех углов равна 180 градусов. Если известны два угла треугольника, третий угол можно найти вычитанием суммы из 180.
Площадь треугольника можно найти по формуле: S = 0.5 * a * b * sin(угол), где a и b - стороны треугольника, а угол - между ними.
Примеры задач и решений

Пример 1:
Дан треугольник ABC, где угол A = 45 градусов, угол B = 60 градусов. Найдем стороны треугольника.
- Найдем третий угол треугольника: угол C = 180 - 45 - 60 = 75 градусов.
- Используем закон синусов: a/sin A = b/sin B = c/sin C.
- Пусть сторона a = 10, тогда sin 45 = b/sin 60 = 10/sin 75.
- Находим b: b = 10 * sin 60 / sin 45 ≈ 11.55.
- Находим c: c = 10 * sin 75 / sin 45 ≈ 14.14.
Таким образом, стороны треугольника ABC равны: a ≈ 10, b ≈ 11.55, c ≈ 14.14.
Пример 2:
Дан треугольник XYZ, где угол X = 30 градусов, угол Y = 75 градусов. Найдем стороны треугольника.
- Найдем третий угол треугольника: угол Z = 180 - 30 - 75 = 75 градусов.
- Используем закон косинусов: a^2 = b^2 + c^2 - 2bc*cos A.
- Пусть сторона b = 8, сторона c = 10, тогда находим сторону a по формуле.
- Вычисляем a: a = √(8^2 + 10^2 - 2*8*10*cos 30) ≈ 9.66.
Таким образом, стороны треугольника XYZ равны: a ≈ 9.66, b = 8, c = 10.
Вопрос-ответ

Можно ли найти стороны треугольника, если известны только углы?
Да, с помощью тригонометрических функций и формулы синусов можно найти стороны треугольника, если известны значения углов. Например, если известно значение одного угла и длины двух сторон, можно найти третью сторону по закону синусов.
Как найти стороны треугольника, если известны углы в радианах?
Для нахождения сторон треугольника по углам в радианах также используется тригонометрия. Необходимо применить формулы синусов или косинусов, чтобы выразить стороны через углы и другие известные значения. Затем можно решить систему уравнений и найти стороны треугольника.
Сколько информации о треугольнике нужно знать, чтобы вычислить его стороны по углам?
Для вычисления сторон треугольника по углам необходимо знать значения хотя бы двух углов и одной стороны. Также можно вычислить стороны, если известны все три угла треугольника. Используя тригонометрические функции, можно получить значения сторон, даже если изначально известны только углы.
Возможно ли решить треугольник, зная только углы, но не имея длин сторон?
Да, при условии, что известно значение хотя бы двух углов и длина одной стороны, можно решить треугольник без знания длин всех сторон. Решение основывается на применении тригонометрических функций и соответствующих формул для нахождения сторон треугольника по углам.



