Теория вероятности – это раздел математики, который изучает случайные события и вероятность их возникновения. Этот инструмент позволяет предсказывать вероятность того или иного исхода, что широко применяется в различных областях, начиная от экономики и физики, и заканчивая медициной и статистикой.
Чтобы рассчитать вероятность события в процентах, нужно знать количество благоприятных исходов и общее число возможных исходов. Далее, просто разделите количество благоприятных исходов на общее число возможных, а затем умножьте на 100%. Таким образом, можно получить вероятность события в процентах.
Знание основ теории вероятности позволит вам более точно оценивать вероятность событий и принимать обоснованные решения на основе анализа данных. Поэтому не стоит пренебрегать изучением этой науки.
Определение теории вероятности
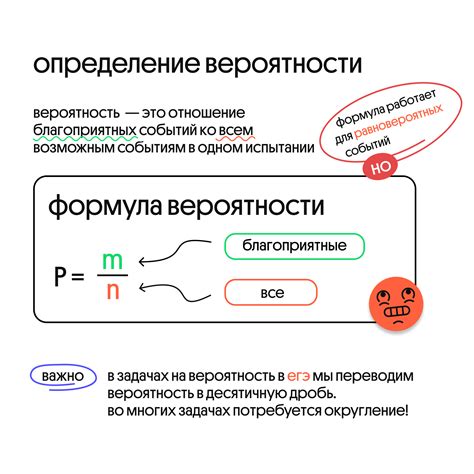
В основе теории вероятности лежит понятие вероятности - численной характеристики возможности наступления того или иного события. Вероятность может быть выражена в виде числа от 0 до 1, где 0 означает невозможность события, а 1 - его непременное наступление.
Теория вероятности является важным инструментом для принятия решений в условиях неопределенности и риска, а также широко применяется в различных областях науки, техники и экономики.
Процентное выражение вероятности

Когда мы говорим о вероятности события, мы часто используем проценты для выражения его вероятности. Для того чтобы рассчитать вероятность события в процентах, необходимо умножить вероятность на 100. Таким образом, вероятность события P в процентах будет равна P*100%. Например, если вероятность выпадения орла при подбрасывании монеты составляет 0.5, то это можно выразить как 0.5*100% = 50%.
Основные понятия и формулы

Теория вероятности изучает случайные события и вероятности их возникновения. Основные понятия включают в себя:
- Элементарное событие - это базовое событие, которое не может быть разбито на более мелкие составляющие.
- Пространство элементарных событий - это множество всех возможных элементарных событий.
- Событие - это некоторое подмножество пространства элементарных событий.
- Вероятность события - это числовая характеристика, отражающая шансы на его возникновение.
Основные формулы для рассчета вероятности включают:
- Формула классической вероятности: P(A) = n(A) / n(S), где n(A) - кол-во благоприятных исходов, n(S) - общее кол-во исходов.
- Формула условной вероятности: P(A|B) = P(A ∩ B) / P(B), где P(A ∩ B) - вероятность совместного наступления событий A и B.
- Формула полной вероятности: P(A) = Σ P(A|Hi)P(Hi), где Hi - разбиение пространства элементарных событий.
Пример расчета вероятности в процентах

Предположим, у нас есть мешок с шариками разных цветов: 10 красных, 5 синих и 3 зеленых. Какова вероятность вытащить красный шарик?
- Найдем общее количество шариков в мешке: 10 + 5 + 3 = 18.
- Найдем количество красных шариков: 10.
- Вероятность вытащить красный шарик равна количеству красных шариков к общему количеству шариков: 10/18 = 0.5555.
- Преобразуем дробь в проценты, умножив ее на 100: 0.5555 * 100 = 55.55%.
Методы расчета вероятности
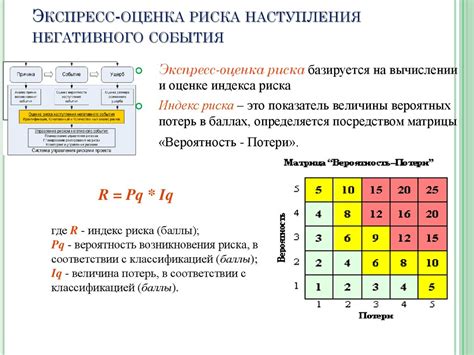
Существуют различные методы расчета вероятности события. Вот несколько из них:
| 1. | Классический метод. Вероятность события равна отношению числа благоприятных исходов к общему числу исходов. |
| 2. | Статистический метод. Вероятность определяется на основе частоты появления события при многократном повторении эксперимента. |
| 3. | Аксиоматический метод. Основывается на аксиомах теории вероятностей и определяет вероятность события как число в интервале от 0 до 1. |
Выбор метода расчета вероятности зависит от конкретной ситуации и доступной информации о событии.
Использование статистики для определения вероятности
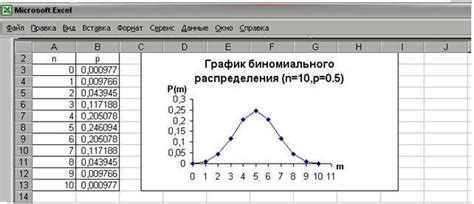
Например, если мы хотим определить вероятность выпадения орла при подбрасывании монеты, мы можем провести серию экспериментов и записать результаты. После этого мы можем посчитать количество раз, когда выпал орел, и разделить это число на общее количество испытаний. Таким образом, мы приблизительно определяем вероятность выпадения орла.
Практическое применение теории вероятности

Теория вероятности широко применяется в различных областях, включая математику, статистику, физику, экономику, биологию и многие другие. Вот несколько примеров практического применения теории вероятности:
| 1. | В финансовой аналитике вероятностные модели помогают прогнозировать будущие цены акций и финансовых инструментов. |
| 2. | В медицине теория вероятности используется для анализа результатов исследований и оценки эффективности лечения. |
| 3. | В сетевом технологическом планировании вероятностные модели помогают оптимизировать распределение ресурсов и улучшить производительность. |
| 4. | В игорной индустрии теория вероятности используется для определения шансов выигрыша и разработки стратегий игры. |
Значение процентов в теории вероятности
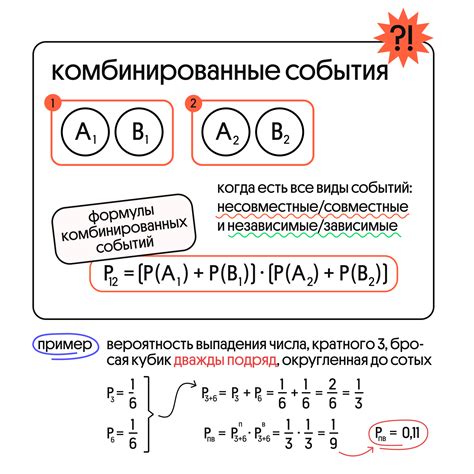
Проценты в теории вероятности используются для измерения вероятности событий в процентном соотношении. Например, если вероятность события равна 0.5, то это означает, что событие происходит в 50% случаев. Это позволяет наглядно представить вероятности и сравнивать их между собой.
Проценты также удобны для сравнения вероятностей разных событий. Например, если событие А имеет вероятность 0.6 (60%), а событие В – 0.3 (30%), то событие А более вероятно, чем событие В. Такая интерпретация делает теорию вероятности более понятной и доступной.
Применение вероятности в реальной жизни

Теория вероятности играет важную роль в реальной жизни, помогая нам принимать рациональные решения на основе вероятностных расчетов. Вот несколько областей, где вероятность широко применяется:
- Финансы: Инвесторы используют вероятностные модели для прогнозирования рыночных трендов и принятия решений об инвестициях.
- Медицина: Врачи могут использовать вероятность для оценки риска заболеваний или на основе статистики выбрать наиболее эффективное лечение.
- Страхование: Страховые компании используют вероятностные методы для определения рисков и расчета страховых взносов.
- Транспорт: Планировщики маршрутов и логистики могут использовать вероятность для оптимизации расписания и снижения задержек.
Это лишь небольшой перечень областей, где вероятность активно применяется, подчеркивая важность понимания и использования данной математической концепции в повседневной жизни.
Вопрос-ответ

Как рассчитать вероятность события в процентах?
Для рассчета вероятности события в процентах нужно сначала определить общее число возможных исходов (N) и число благоприятных исходов (n), после чего применить формулу: P = (n / N) * 100%. Таким образом, вычисляя отношение числа благоприятных исходов к общему числу исходов и умножая его на 100%, можно получить вероятность события в процентах.
Можно ли выразить теорию вероятности в процентах?
Да, теорию вероятности можно выразить в процентах. Вероятность события может быть представлена в процентах, что позволяет лучше понимать и оценивать вероятность наступления данного события. Просто нужно правильно рассчитать соотношение числа благоприятных исходов к общему числу исходов и умножить на 100%.
Как интерпретировать результаты расчета вероятности в процентах?
После выполнения расчетов вероятности события в процентах, полученный результат можно интерпретировать следующим образом: если вероятность события равна, например, 70%, то это означает, что событие имеет большую вероятность наступления, чем события с вероятностью 50% или меньше. Таким образом, процент вероятности позволяет оценить возможность наступления события с точки зрения вероятности.



