Проверка параллельности прямых - важное понятие в задачах начертательной геометрии, которое позволяет определить, пересекаются ли две прямые или они параллельны. Понимание этого понятия необходимо для построения различных геометрических фигур и решения задач на плоскости.
Для проверки параллельности прямых существует несколько способов, один из наиболее распространенных - это использование углов. Если две прямые параллельны, то все углы между ними будут равными. Это свойство можно использовать для проверки параллельности прямых на плоскости.
Параллельность прямых в геометрии
Чтобы проверить параллельность двух прямых, используются определенные правила и свойства. Например, если две прямые пересекаются с третьей прямой таким образом, что внутренние углы с одной стороны от этой пересекающей прямой являются смежными и равными, то рассматриваемые прямые параллельны.
Как проверить параллельность прямых
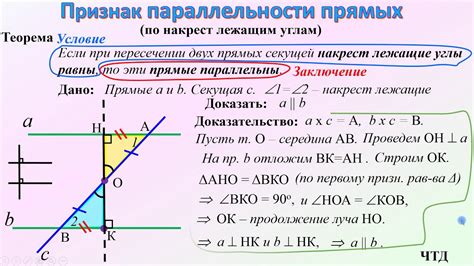
| Параллельные прямые | Непараллельные прямые |
| Угол 1 = Угол 2 | Угол 1 ≠ Угол 2 |
Кроме того, параллельные прямые имеют одинаковые наклоны. Используйте этот признак для проверки параллельности прямых.
Вопрос-ответ

Как определить, что две прямые параллельны в начертательной геометрии?
Две прямые в начертательной геометрии считаются параллельными, если они не пересекаются и не лежат на одной прямой. Проверить это можно по нескольким признакам: совпадают ли углы наклона прямых, совпадают ли углы наклона биссектрис углов, лежащих на прямых, или равны ли количества прямых углов, образуемых этими прямыми с параллельными прямыми, например с перпендикуляром. Если хотя бы одно из этих условий выполняется, прямые считаются параллельными.
Какое значение имеет параллельность прямых в начертательной геометрии?
Параллельные прямые в начертательной геометрии играют важную роль при построении различных фигур, расположении геометрических объектов относительно друг друга и в решении задач на нахождение расстояний. Знание того, как проверить параллельность прямых, поможет правильно решать геометрические задачи и строить фигуры таким образом, чтобы сохранять определенные пропорции и расположение элементов в пространстве.



