Треугольник – одна из основных фигур в геометрии, характеризующаяся тремя сторонами и тремя углами. По величине своих углов треугольники могут быть остроугольными, прямоугольными и тупоугольными. Тупоугольный треугольник – это такой треугольник, у которого один из углов больше 90 градусов.
Для определения, является ли треугольник тупоугольным, следует изучить длины его сторон и применить теорему косинусов. Этот метод основан на сравнении длин сторон треугольника и вычислении косинусов углов.
Изучение геометрических фигур и их свойств позволяет лучше понимать мир вокруг нас и применять полученные знания в повседневной жизни.
Треугольник: понятие и свойства
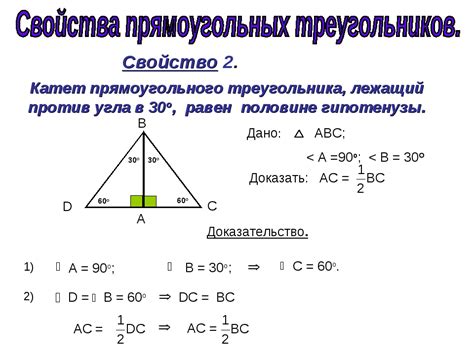
Основные свойства треугольника:
- Сумма углов треугольника равна 180 градусам.
- Сторона треугольника не может быть длиннее суммы двух других сторон и не может быть короче разности двух других сторон.
- Геометрическое свойство треугольника: внутренние углы треугольника могут быть остроугольными, тупоугольными или прямоугольными.
- Тупоугольный треугольник - треугольник, у которого один из углов больше 90 градусов.
Стороны треугольника и их взаимосвязи
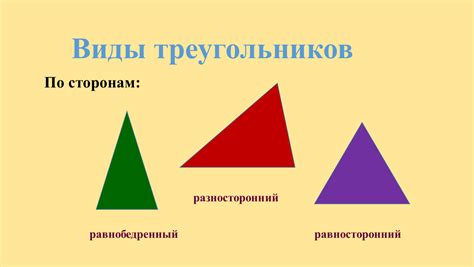
В любом треугольнике имеются три стороны, которые обозначаются буквами a, b и c. Стороны треугольника связаны определенными соотношениями и свойствами. Например, сумма любых двух сторон треугольника должна быть больше третьей стороны: a + b > c, a + c > b, b + c > a.
Помимо этого, в треугольнике существует понятие наибольшей и наименьшей стороны. Наибольшая сторона обычно обозначается как гипотенуза (c), а остальные стороны – как катеты (a и b) в прямоугольном треугольнике. Это позволяет определять тип треугольника: прямоугольный, остроугольный, тупоугольный, а также их свойства.
Зная длины сторон треугольника, можно определить его тип. Например, если квадрат наибольшей стороны (c^2) равен сумме квадратов двух остальных сторон (a^2 + b^2), то треугольник является прямоугольным. На основании этого можно также выяснить, является ли треугольник тупоугольным по длинам его сторон.
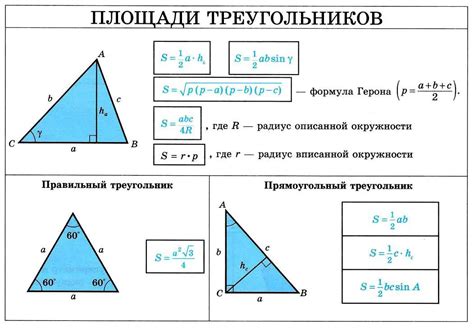
Формула площади треугольника
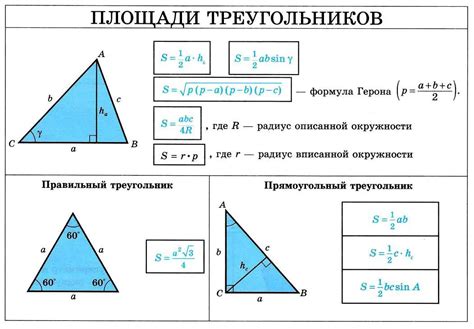
Площадь треугольника можно вычислить по формуле:
S = (a * b * sin(C)) / 2
где:
- S - площадь треугольника;
- a и b - длины сторон треугольника;
- C - угол между сторонами a и b (можно использовать sin, если угол измеряется в радианах).
Эта формула позволяет находить площадь треугольника, зная длины его сторон и угол между ними. Она основана на половине произведения длин двух сторон на синус угла между ними.
Критерии тупоугольного треугольника
| Способ | Условие |
|---|---|
| Теорема косинусов | Если квадрат одной из сторон треугольника больше суммы квадратов двух других сторон, то угол против этой стороны будет тупым. |
| Сравнение длин сторон | Если самая большая сторона треугольника больше суммы двух других сторон, то треугольник является тупоугольным. |
Способы определения типа треугольника
Для определения типа треугольника можно использовать различные методы, включая:
- По длинам сторон: если одна из сторон больше суммы двух других сторон, то треугольник тупоугольный.
- По углам: если угол между двумя сторонами больше 90 градусов, то треугольник тупоугольный.
- По теореме косинусов: с помощью длин сторон и косинуса угла можно определить тип треугольника.
Построение треугольника по его сторонам
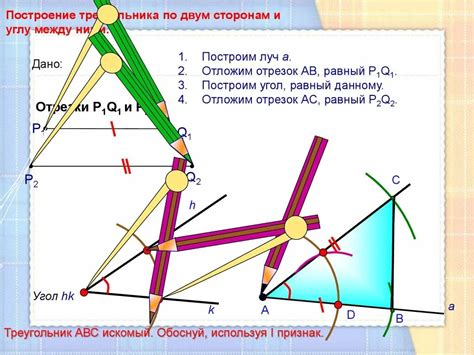
Для построения треугольника по заданным длинам его сторон необходимо выполнить следующие шаги:
1. Взять линейку или другой инструмент для измерения и отложить на листе бумаги отрезки, соответствующие длинам сторон треугольника, их можно обозначить буквами a, b, c.
2. Начертить на листе основу треугольника – отрезок длиной a.
3. От точки начала основы (одного из концов отрезка a) отложить вправо отрезок b под углом, равным углу, образуемому сторонами a и b. Точка конца отложенного отрезка будет первой вершиной треугольника.
4. Из последней точки отложить влево отрезок c под углом, равным углу, образуемому сторонами a и c. Точка конца этого отрезка будет второй вершиной треугольника.
5. Провести линию от второй вершины к началу основы – это третья вершина треугольника.
6. Проверить, что длины полученных сторон соответствуют заданным значениям a, b, c. Если все сходится, то треугольник построен верно. В противном случае, вероятно, введены неверные значения длин сторон.
Примеры задач на определение типа треугольника
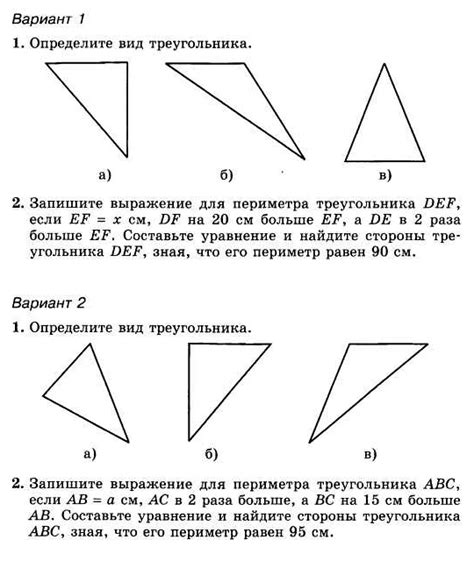
2. Известно, что треугольник со сторонами a = 8, b = 10, c = 12 является прямоугольным. Проверить это утверждение.
3. Найдите треугольник с сторонами a = 7, b = 24, c = 25. Определите его тип (остроугольный, тупоугольный, прямоугольный).
Геометрические методы анализа треугольников

Треугольник является тупоугольным, если квадрат длины самой длинной стороны больше суммы квадратов длин двух других сторон.
Для этого можно применить следующий алгоритм:
| Шаг | Действие |
|---|---|
| 1 | Найдите длины всех трёх сторон треугольника. |
| 2 | Выберите самую длинную сторону и найдите квадрат ее длины. |
| 3 | Найдите сумму квадратов длин двух оставшихся сторон. |
| 4 | Сравните значение из шага 2 со значением из шага 3. |
| 5 | Если квадрат длины самой длинной стороны больше суммы квадратов длин двух других сторон, то треугольник является тупоугольным. |
Условия существования тупоугольного треугольника
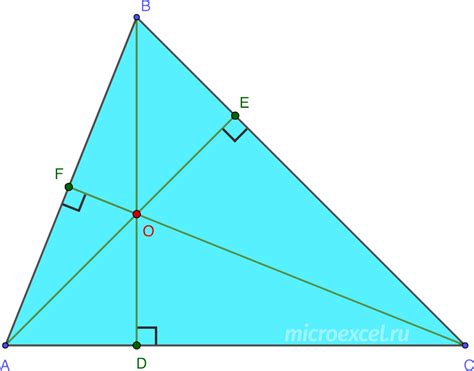
Для того чтобы треугольник был тупоугольным, необходимо, чтобы квадрат длины самой длинной стороны треугольника был больше суммы квадратов длин двух остальных сторон.
Формула для проверки условия существования тупоугольного треугольника выглядит следующим образом:
a^2 > b^2 + c^2, где a – самая длинная сторона треугольника, b и c – две оставшиеся стороны треугольника.
Если данное неравенство выполняется, то треугольник является тупоугольным.
Практическое применение знания о тупоугольных треугольниках

Знание о тупоугольных треугольниках может быть полезно в различных областях, включая геометрию, инженерные расчеты и строительство. Например, при проектировании зданий и мостов необходимо учитывать возможность возникновения тупоугольных треугольников для правильного распределения нагрузок и обеспечения стабильности конструкции.
В геодезии и картографии знание о тупоугольных треугольниках позволяет более точно определять расстояния и углы на местности, что необходимо для составления точных карт и планов местности.
Также понимание особенностей тупоугольных треугольников может пригодиться при решении геометрических задач и задач оптимизации в различных инженерных и математических дисциплинах.
Вопрос-ответ

Как определить, является ли треугольник тупоугольным по длинам его сторон?
Для определения, является ли треугольник тупоугольным по длинам его сторон, необходимо проверить выполнение теоремы косинусов. Если в треугольнике сумма квадратов двух меньших сторон меньше квадрата самой большой стороны, то треугольник является тупоугольным.
Какая формула позволяет определить тупоугольный ли треугольник?
Для определения, является ли треугольник тупоугольным, можно воспользоваться формулой косинуса угла треугольника. Если квадрат самой длинной стороны треугольника больше суммы квадратов двух других сторон, то треугольник тупоугольный.
Какие принципы лежат в основе определения тупоугольности треугольника по длинам его сторон?
Основным принципом определения тупоугольности треугольника по длинам его сторон является применение теоремы косинусов, которая устанавливает взаимосвязь между длинами сторон треугольника и косинусами его углов.
Как можно использовать теорему косинусов для определения тупоугольности треугольника?
Для определения, является ли треугольник тупоугольным, можно использовать теорему косинусов для вычисления косинуса угла между сторонами треугольника. Если косинус этого угла отрицателен, то треугольник тупоугольный.
Существует ли другой подход к определению тупоугольности треугольника, помимо формулы косинусов?
Помимо формулы косинусов, для определения тупоугольности треугольника можно также использовать формулу синуса и теорему синусов, но обычно формула косинусов является более удобной и эффективной в данной задаче.



