В мире математики существует множество функций, которые позволяют нам оценивать и анализировать различные явления и процессы. Одной из таких функций является синус, которая изучает зависимость между углом и соответствующим ему отношением противоположной стороны к гипотенузе в прямоугольном треугольнике.
Одним из интересных аспектов связанных с синусом является определение его значения при конкретных углах. В данной статье мы рассмотрим значение синуса при угле в 106 градусов. Это значение может быть полезно и применяться в различных областях, начиная от геометрии и заканчивая физикой и инженерией.
Если обратиться к таблице значений синуса, можно увидеть, что значение синуса при угле 106 градусов составляет некоторое число в интервале от -1 до 1. Однако, просто зная значение синуса, мы не можем окончательно оценить треугольник или явление, которое описывается этой функцией. Для более точной оценки, нам необходимы формулы расчета синуса при данном угле.
Значение и применение синуса угла 106 градусов
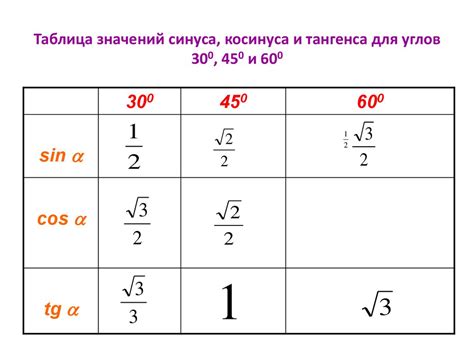
Величина, которая сопутствует углам и принадлежит к категории тригонометрических функций, имеет несомненное значение и применение в различных сферах науки и практики. Когда мы рассматриваем синус угла 106 градусов, мы обращаемся к части синусоиды, которая определена данной величиной угла. Далее мы представим некоторые конкретные области, в которых значительное значение имеет синус угла 106 градусов.
Инженерия: Синус 106 градусов применяется в области инженерии при решении задач, привязанных к построению, например, к проектированию зданий и сооружений с учетом наклона или отклонения в определенном направлении.
Архитектура: Архитекторы активно используют синус 106 градусов для создания структур, обеспечивающих определенный угол наклона или инклинацию в определенных точках здания.
Физика: В физике синус 106 градусов может быть применен для расчета углов падения света или других видов волновых передач и преломления, что позволяет определить направление и интенсивность их движения.
Геодезия: В геодезии синус 106 градусов может использоваться для определения углов между горизонтальными и вертикальными плоскостями при измерении или прокладке территорий.
Синус 106 градусов и его значения находят широкое применение во многих других областях науки и практики, где требуется учет углов и их влияния на окружающие объекты и процессы.
Значение синуса 106 градусов в таблице
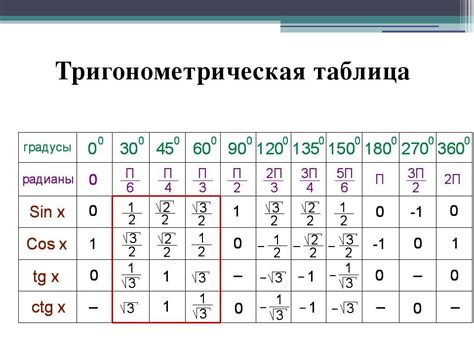
Данная часть статьи посвящена представлению значений синуса 106 градусов в удобной таблице. Здесь можно найти числовые данные, которые соответствуют этому углу и помогут в дальнейших вычислениях и анализе. Для облегчения работы вместо использования сложных формул и расчетов, данная таблица предоставляет простые и понятные числовые значения синуса 106 градусов.
Нижеприведенные числа представляют значения синуса 106 градусов и помогут вам легко получить необходимую информацию без необходимости в ручных вычислениях:
Значение синуса 106 градусов: вы можете найти его в соответствующей ячейке таблицы.
Таблица значений синуса 106 градусов обеспечивает наглядное и простое представление данных, которые можно легко использовать в различных математических задачах и научных исследованиях. Благодаря этой таблице вы сможете мгновенно получить значение синуса 106 градусов без лишней трудности и временных затрат.
Как вычислить значение синуса для угла 106 градусов?

Для начала нам потребуется преобразовать угол 106 градусов в радианы, поскольку синусовая функция обычно применяется к углам, выраженным в радианах. Радианы измеряют дугу окружности, охватываемую этим углом. Для этого умножим величину угла в градусах на коэффициент преобразования: π/180 (пи/180).
После преобразования угла в радианы, мы можем использовать радианную формулу синуса для вычисления значения. Формула синуса гласит: sin(x) = opposite/hypotenuse, где opposite - длина стороны противоположной углу x, а hypotenuse - гипотенуза треугольника.
Теперь, чтобы вычислить значение синуса для угла 106 градусов, необходимо знать длины сторон противоположной и гипотенузы. В зависимости от контекста задачи, эти значения могут быть предоставлены или должны быть вычислены основываясь на других известных данных.
Важно помнить, что значения синуса находятся в диапазоне от -1 до 1, поэтому результат вычисления может быть отрицательным или положительным в зависимости от взаимного расположения угла и сторон треугольника. При решении задачи также следует обратить внимание на систему углов, используемую в контексте – градусы или радианы.
Вопрос-ответ

Как посчитать значение синуса 106 градусов?
Значение синуса 106 градусов можно рассчитать, используя таблицу значений тригонометрических функций или математическую формулу. В таблице найдите угол 106 градусов и посмотрите соответствующее значение синуса. Если в таблице нет точного значения для 106 градусов, можно приблизить его из ближайших значений. Например, для 105 градусов и 110 градусов. Формула для расчета синуса также может быть использована: sin(106°) = sin(180° - 106°) = sin(74°). Зная значение синуса 74 градусов, можно вычислить значение для 106 градусов.
Где найти таблицу значений синуса?
Таблицу значений синуса можно найти в учебниках по тригонометрии или математике, в собраниях формул и таблиц или в интернете. Многие онлайн-ресурсы предоставляют подробные таблицы значений тригонометрических функций для различных углов, включая значение синуса. При использовании таблицы необходимо обратить внимание на единицы измерения угла (обычно градусы) и точность значений, которые указаны в таблице.
Как использовать значения синуса из таблицы?
Для использования значений синуса из таблицы, необходимо найти угол, для которого вы хотите вычислить синус, и смотреть на соответствующее значение синуса в таблице. Например, если вам нужно найти синус угла 60 градусов, найдите этот угол в таблице и посмотрите значение синуса. Если точного значения нет, можно использовать приближенное значение из ближайших углов. Например, для синуса 62 градусов можно использовать значение из таблицы для 60 градусов и 65 градусов. Это приближение будет достаточно точным, если угол не очень близок к особым значениям, таким как 0°, 90°, 180° и т. д.



