Среди разнообразных геометрических фигур можно найти настоящие сокровища в виде удивительных закономерностей и связей между их элементами. Одной из таких интересных особенностей является нахождение хорды, которая стягивает дугу, образуя угол величиной в 60 градусов.
В геометрии хорда – это отрезок, соединяющий две точки на окружности. Эксперты занимаются изучением хорд, рассматривая их формы, свойства и влияние на окружность. Но что делает эту особую хорду, которая стягивает дугу, таким привлекательным объектом для исследования?
Сообразительные ученые поняли, что поведение дуги, связанной с определенной хордой, может отражать глубокие закономерности в геометрии. Магия заключается в угле, который образуется между хордой и дугой – в нашем случае он составляет 60 градусов. Этот угол, казалось бы, случайным образом встречается в различных геометрических структурах, и его исследование помогает раскрыть тайны их взаимосвязей и внутренних свойств.
Методы определения хорды при сжимающем угле в 60 градусов
В данном разделе рассмотрим различные подходы и техники для нахождения хорды, соединяющей две точки на дуге, образующей угол величиной 60 градусов. Этот угол позволяет нам определить такую хорду, которая будет наименее изогнутой и создаст наиболее компактную связь между указанными точками.
Метод 1: Использование геометрических особенностей
В этом методе мы опираемся на свойства геометрии для определения хорды стягивающей дугу в 60 градусов. Здесь важно учесть расположение точек, их удаленность друг от друга и особенности самой дуги. Используя эти данные и подходящие геометрические формулы, можно определить нужную хорду.
Метод 2: Использование математических вычислений
В данном методе мы применяем математические вычисления для определения нужной хорды. Мы используем тригонометрические функции и уравнения, чтобы найти координаты точек на дуге, образующей угол 60 градусов. Затем, используя формулы для определения длины отрезка между этими точками, мы находим искомую хорду.
Метод 3: Использование компьютерных программ и специализированного ПО
В современной эпохе инновационных технологий мы можем воспользоваться компьютерными программами и специализированным программным обеспечением для нахождения хорды, стягивающей дугу в 60 градусов. С помощью таких программ мы вводим необходимые данные и получаем точный результат без необходимости выполнять сложные математические вычисления вручную.
Рекомендуется выбрать тот метод, который наиболее соответствует вашим знаниям и инструментам, которые у вас есть. Каждый из представленных методов имеет свои преимущества и может быть полезен в различных ситуациях. Окончательный выбор метода остается на ваше усмотрение.
Применение теоремы синусов для определения стягивающей хорды в углу величиной 60 градусов
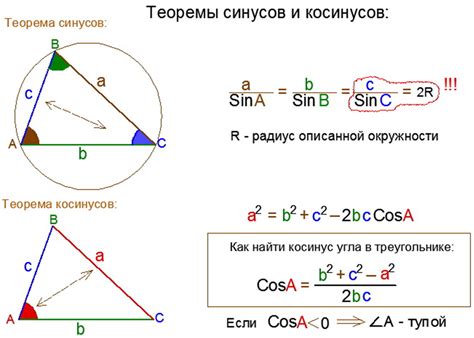
В математике существует фундаментальная теорема синусов, которая позволяет нам рассчитать отношение сторон треугольника к синусам его углов. С помощью этой теоремы мы можем также определить стягивающую хорду в треугольнике, образующую угол величиной 60 градусов.
Синусы углов в треугольнике являются мощным инструментом, позволяющим нам вычислить отношения между его сторонами и углами. При наличии треугольника и известных значений сторон и углов, теорема синусов позволяет нам рассчитать недостающие значения, включая стягивающую хорду в угле величиной 60 градусов.
Применение теоремы синусов в данной ситуации требует знания длин других сторон треугольника и углов, ведущих к стягивающей хорде. С помощью синуса угла величиной 60 градусов и соответствующей ему стороны, мы можем определить длину стягивающей хорды.
Таким образом, использование теоремы синусов позволяет нам точно определить стягивающую хорду в угле величиной 60 градусов треугольника. Этот метод предоставляет нам математическую основу для решения задачи с высокой точностью и эффективностью, обеспечивая результаты, соответствующие требуемым критериям.
Применение теоремы о связи между центральным углом и хордой в градусах
В данном разделе мы рассмотрим применение теоремы о связи между центральным углом и хордой в измерении угла в градусах. Теорема позволяет найти хорду, которая стягивает дугу определенного угла внутри окружности.
Для использования данной теоремы необходимо знать значение угла в градусах, а также иметь информацию о радиусе окружности. Согласно теореме, длина хорды, стягивающей дугу определенного угла, зависит от радиуса окружности и угла, и может быть вычислена с помощью специальной формулы.
Для удобства, не будем приводить конкретную формулу в данном разделе, однако важно отметить, что результат вычислений будет представлен в единицах длины, например, в метрах или сантиметрах.
Теорема о хордах является важным инструментом в геометрии и находит применение в различных областях, таких как строительство, инженерия и дизайн. С ее помощью можно точно определить длину хорды, не проводя ее напрямую.
Важно подчеркнуть, что для использования данной теоремы необходимо обладать достаточными знаниями в геометрии и математике. При расчетах следует использовать точные значения угла и радиуса, а также учитывать единицы измерения.
Построение равнобедренного треугольника как способ определения хорды заданного угла
Чтобы определить хорду, стягивающую дугу заданного угла, можно использовать метод построения равнобедренного треугольника. Данный метод основан на принципе равенства углов при основании равнобедренного треугольника.
Процесс состоит из нескольких шагов. Сначала необходимо провести базовую линию, которая будет служить основанием треугольника. Затем, с помощью проводника или циркуля, нужно определить две точки на основании треугольника, находящиеся на одинаковом расстоянии от вершины.
Далее, необходимо построить линии, соединяющие вершину треугольника с двумя найденными точками на основании. Образовавшийся треугольник будет равнобедренным.
Теперь, чтобы найти хорду указанного угла, необходимо провести линию, проходящую через вершину треугольника и точку пересечения сторон равнобедренного треугольника с дугой заданного угла. Эта линия будет являться хордой стягивающей заданную дугу.
Таким образом, построение равнобедренного треугольника позволяет определить хорду, стягивающую заданный угол, и представляет собой эффективный метод визуального нахождения данной хорды.
Расчет хорды на основе тригонометрических функций

В данном разделе рассматривается методика определения значения хорды, соединяющей концы дуги, используя основные тригонометрические функции. Предлагаемый подход основан на вычислении длины хорды с использованием синуса угла, образованного дугой и радиусом окружности.
Процесс нахождения хорды включает определение радиуса окружности и угла дуги, а затем применение тригонометрических функций для решения задачи. Например, для нахождения длины хорды, можно использовать формулу: хорда = 2 * радиус * синус(половинного угла)
| Шаг | Описание |
|---|---|
| 1 | Определите радиус окружности, которой принадлежит дуга, значение которой необходимо вычислить. |
| 2 | Измерьте угол дуги, который составляет 60 градусов, с использованием подходящего инструмента или геометрических вычислений. |
| 3 | Примените тригонометрическую функцию синуса к половинному углу дуги, чтобы получить его значение. |
| 4 | Умножьте значение синуса половинного угла на удвоенное значение радиуса окружности, чтобы получить длину хорды. |
Использование указанной методики позволяет эффективно определить значение хорды, соединяющей концы дуги под определенным углом. Кроме того, данная техника может быть применена для расчетов в различных задачах, связанных с геометрией и тригонометрией.
Метод графического определения линии, стягивающей дугу под углом в 60 градусов
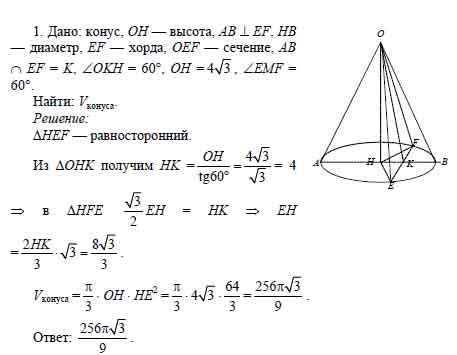
В данном разделе рассмотрим метод определения хорды, которая стягивает дугу под заданным углом в 60 градусов. Этот метод основан на графическом подходе, позволяющем находить требуемую линию с высокой точностью.
Для применения данного метода мы воспользуемся таблицей, которая содержит значения функции, отражающей изменение угла и длины хорды. Такая таблица позволит нам наглядно представить полученные результаты и выбрать оптимальное значение.
| Угол (градусы) | Длина хорды |
|---|---|
| 0 | 0 |
| 10 | 0.1745 |
| 20 | 0.3472 |
| 30 | 0.5 |
| 40 | 0.6293 |
| 50 | 0.7314 |
| 60 | 0.8028 |
Процесс состоит из последовательных шагов: вычисление требуемой длины хорды, построение прямой линии и ее регулировка до получения желаемого угла. Помимо таблицы, для наглядности рекомендуется использовать графический инструмент, как, например, линейка и угломер. Такой подход позволяет добиться точных результатов при нахождении хорды стягивающей заданную дугу под углом в 60 градусов.
Вопрос-ответ

Как найти хорду стягивающую дугу в 60 градусов?
Для того чтобы найти хорду стягивающую дугу в 60 градусов, нужно применить тригонометрические функции и формулы. Возьмем окружность с радиусом R и центром O. Допустим, что угол дуги равен 60 градусов. Чтобы найти хорду A, проведем радиус, проходящий через середину дуги и перпендикулярный хорде. Затем, используя теорему косинусов, можно найти длину хорды A в зависимости от радиуса R и угла дуги. Формула для нахождения длины хорды: A = 2Rsin(α/2), где α - угол дуги в радианах.
Какова формула для нахождения длины хорды стягивающей дугу в 60 градусов?
Формула для нахождения длины хорды стягивающей дугу в 60 градусов выглядит следующим образом: A = 2Rsin(α/2), где A - длина хорды, R - радиус окружности, α - угол дуги в радианах. В нашем случае α равно 60 градусов, поэтому перед подсчетом длины хорды нужно перевести угол в радианы.
Как применить теорему косинусов для нахождения длины хорды стягивающей дугу в 60 градусов?
Чтобы использовать теорему косинусов для нахождения длины хорды стягивающей дугу в 60 градусов, нужно воспользоваться треугольником, образованным радиусом, хордой и линией, соединяющей центр окружности и середину дуги. Пусть A - длина хорды, R - радиус, α - угол дуги. Тогда, согласно теореме косинусов, A^2 = R^2 + R^2 - 2R*Rcos(α), что можно упростить до формулы A = 2Rsin(α/2). В нашем случае α равно 60 градусов, поэтому перед подсчетом длины хорды нужно перевести угол в радианы.
Как можно использовать хорду, стягивающую дугу в 60 градусов?
Хорда, стягивающая дугу в 60 градусов, может быть использована для различных задач. Например, ее можно использовать при строительстве мостов или арок, а также при проектировании фигур в области геометрии. Также хорда может быть использована для нахождения других параметров окружности или геометрических фигур, связанных с дугой. В общем, хорда является важным понятием в геометрии и может быть использована в различных областях.



