Геометрия – один из фундаментальных разделов математики, который изучает пространственные отношения и фигуры. Для учеников 7 класса особенно важно освоить основные принципы геометрии, включая различные теоремы и правила.
Одной из основных теорем, которую изучают школьники на этом этапе обучения, является теорема о сумме углов в треугольнике. Согласно этой теореме, сумма всех углов треугольника равна 180 градусам. Это правило помогает анализировать геометрические фигуры и решать задачи на построение и расчет площадей.
Основные принципы теоремы
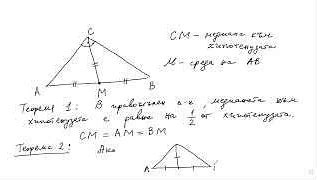
2. Доказательство: Каждая теорема требует строгое доказательство, основанное на логике и геометрических принципах. Доказательство должно быть четким и логичным.
3. Гипотеза: Теорема формулируется на основе предположений и гипотез о свойствах геометрических объектов.
Геометрия и её значение
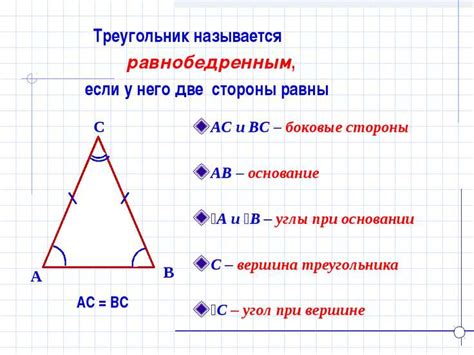
Знания геометрии помогают людям понимать мир вокруг себя, строить сооружения, работать с картами, проектировать и создавать объекты в разных сферах деятельности. Важно уметь применять геометрию для анализа и решения задач, для построения логических цепочек и доказательств.
Изучение геометрии развивает мышление, воображение, логическое мышление и способность анализировать информацию. Поэтому знание основ геометрии является важным элементом в образовании и он пригодится в различных сферах жизни.
Сформулированные утверждения

- Основная теорема геометрии для 7 класса - теорема Пифагора.
- Сумма квадратов катетов в прямоугольном треугольнике равна квадрату гипотенузы: a^2 + b^2 = c^2.
- Геометрическая теорема о равенстве углов - углы, образованные параллельными прямыми и пересекающей их секущей, равны.
- Теорема о сумме углов в треугольнике - сумма углов треугольника равна 180 градусам.
- Теорема о равенстве углов при параллельных прямых - соответственные углы при пересечении параллельных прямых равны.
Примеры использования
Пример 1: По теореме Пифагора можно вычислить длину гипотенузы прямоугольного треугольника, если известны длины его катетов.
Пример 2: С помощью теоремы о равных углах у двух пересекающихся прямых можно найти значение неизвестного угла.
Пример 3: При использовании теоремы о равенстве треугольников можно доказать равенство сторон и углов в треугольниках.
Решение геометрических задач

Для решения геометрических задач на основе теоремы по геометрии для 7 класса, следует следовать определенным шагам:
- Внимательно прочитать условие задачи и изобразить все данные на чертеже.
- Используя известные теоремы и правила, вывести соответствующие углы или длины отрезков.
- Применить свойства фигур (треугольников, четырехугольников) для нахождения недостающих элементов.
- Проверить полученные значения с помощью проверочных расчетов или условий задачи.
- Сформулировать окончательный ответ на вопрос задачи.
Применение в повседневной жизни

Знание геометрии необходимо не только в школьных уроках, но и в повседневной жизни. Например, при постройке или ремонте дома нам приходится работать с различными фигурами и измерениями. Благодаря теоремам по геометрии, мы можем правильно расположить мебель в комнате, вычислить необходимое количество материалов для отделки или строительства, а также решать практические задачи. Кроме того, понимание основ геометрии помогает развивать логическое и абстрактное мышление, что полезно в решении различных задач в жизни.
Для наглядного примера, представим себе ситуацию, когда нам нужно рассчитать площадь комнаты для поклейки обоев. Знание теоремы о площади прямоугольника позволит нам легко определить необходимое количество рулонов обоев для данной комнаты. Таким образом, понимание геометрии помогает нам применять математические знания в повседневных ситуациях и делает нашу жизнь более удобной.
| Пример | Применение |
|---|---|
| Рассчет площади пола | Выбор нужного количества напольного покрытия |
| Изучение планов | Понимание пространственных отношений и фигур |
| Определение объема | Расчет необходимого количества материалов |
Вопрос-ответ

Что такое теорема по геометрии?
Теорема по геометрии – это математическое утверждение, которое описывает особенности геометрических фигур и их свойств. В геометрии для 7 класса теоремы помогают понять и решать задачи на нахождение длин отрезков, углов, площадей и других характеристик фигур.
Какие основные принципы лежат в основе теорем по геометрии для 7 класса?
Основные принципы теорем по геометрии для 7 класса включают в себя принципы подобия треугольников, равенства углов, равенства сторон, теорему Пифагора, теорему о сумме углов треугольника и другие правила и свойства геометрии.
Как применить теорему о сумме углов треугольника на практике?
Теорема о сумме углов треугольника гласит, что сумма всех углов в треугольнике равна 180 градусам. Поэтому применяя эту теорему на практике, можно находить неизвестные углы в треугольнике, зная значения других углов. Также, с помощью этой теоремы можно проводить доказательства в геометрических задачах.
Можете ли вы привести пример задачи, в которой применяется теорема Пифагора?
Конечно! Например, в задаче о прямоугольном треугольнике со сторонами a=3 и b=4, нужно найти длину гипотенузы с помощью теоремы Пифагора: c^2 = a^2 + b^2, где c - гипотенуза. Подставляя значения a=3 и b=4, получаем c^2 = 3^2 + 4^2, т.е. c^2 = 9 + 16, откуда c^2 = 25 и c = 5. Таким образом, длина гипотенузы в этом треугольнике равна 5.



