В мире окружающих нас чисел и формул порой сложно уловить те незримые связи, которые скрываются в глубинах последовательностей. Однако, благодаря математическим методам и анализу данных, мы можем раскрыть тайны и распознать закономерности, лежащие за ними.
Одним из важных понятий, которое поможет нам понять и описать последовательности чисел, является геометрическая прогрессия. Геометрическая прогрессия представляет собой последовательность чисел, в которой каждый следующий элемент получается умножением предыдущего элемента на постоянное число, называемое знаменателем. Для того чтобы узнать этот знаменатель и доказать, что данная последовательность является геометрической прогрессией, существует несколько методов и подходов.
Знание законов геометрической прогрессии не только помогает нам понять структуру последовательности чисел, но и находит своё применение в различных областях: от анализа финансовых данных до определения физических закономерностей.
Основные понятия и формулы для определения геометрической прогрессии последовательности

Основные понятия:
- Первый член прогрессии: это начальный элемент последовательности, обозначенный a₁;
- Знаменатель прогрессии: это число q, на которое умножается каждый предыдущий член, чтобы получить следующий;
- n-й член прогрессии: это элемент последовательности с номером n, обозначенный aₙ;
- Общий член прогрессии: это формула, позволяющая вычислить любой член прогрессии по его номеру, а₁ и q.
Формулы:
Общий член прогрессии может быть выражен двумя способами:
1. Формула для вычисления n-го члена прогрессии:
aₙ = a₁ * q^(n-1)
где a₁ - первый член прогрессии, q - знаменатель прогрессии, n - номер члена прогрессии.
2. Формула для вычисления q (знаменателя прогрессии):
q = aₙ / aₙ₋₁
где aₙ - n-й член прогрессии, aₙ₋₁ - (n-1)-й член прогрессии.
Зная первый член прогрессии и знаменатель, мы можем легко вычислить n-й член прогрессии или, наоборот, определить знаменатель по значениям двух последовательных членов.
Основы геометрической прогрессии

Первым шагом в определении геометрической прогрессии является распознавание основного шаблона, представленного последовательностью чисел, в которой каждый последующий член является произведением предыдущего на постоянный множитель. Этот множитель, также известный как "знаменатель прогрессии", определяет зависимость между всеми элементами последовательности.
Для определения того, является ли данная последовательность геометрической прогрессией необходимо установить, что каждый член последовательности является произведением предыдущего члена на знаменатель прогрессии. Если данное условие выполняется для всех элементов последовательности, можно уверенно сказать, что мы имеем дело с геометрической прогрессией.
Другим важным элементом определения геометрической прогрессии является начальный член последовательности, также известный как "первый член" или "нулевой член". Этот член является отправной точкой для построения всей последовательности и определяет начальное значение. Обычно он указывается явно, чтобы исключить неоднозначности в указании начала последовательности.
Итак, геометрическая прогрессия - это последовательность чисел, в которой каждый член является произведением предыдущего на постоянный множитель. Определение геометрической прогрессии сводится к определению этого постоянного множителя и явного указания начального члена. Распознавание геометрической прогрессии позволяет проводить различные аналитические операции, такие как вычисление любого члена, суммы членов и нахождения общего количества элементов в последовательности.
Вычисление общего члена геометрической прогрессии: секреты расчета

- Первый шаг: Запишите известные значения последовательности чисел, отметив их как a1, a2, a3, и так далее.
- Второй шаг: Найдите отношение между последовательными значениями, используя формулу R = an / an-1, где R - это пропорция между an и предыдущим членом последовательности an-1.
- Третий шаг: Вычислите R путем взятия корня n-го порядка из полученных отношений между значениями последовательности. Значение R позволяет определить общий множитель последовательности.
- Четвертый шаг: Используя полученное значение R и известное значение a1, вычислите общий член геометрической прогрессии с помощью формулы an = a1 * Rn-1, где an - это n-ый член последовательности.
Зная эти шаги и применяя соответствующие формулы, вы сможете расчитать общий член геометрической прогрессии и дальше анализировать и предсказывать последовательность чисел.
Сумма членов геометрической прогрессии: как вычислить и понять
Сумма членов геометрической прогрессии - это общая сумма всех чисел в последовательности. Она может быть полезна, когда мы хотим найти сумму большого числа членов или оценить общий результат. Как найти эту сумму? Существует формула, которая позволяет нам вычислить сумму геометрической прогрессии, используя начальный член, знаменатель и количество членов последовательности.
- Начальный член геометрической прогрессии обозначается символом a.
- Знаменатель - символ q, стоящий в знаке умножения.
- Количество членов геометрической прогрессии обозначается символом n.
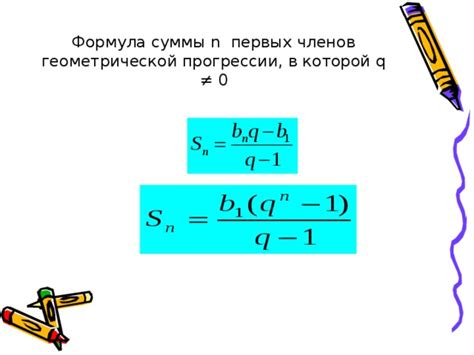
Формула для вычисления суммы членов геометрической прогрессии имеет вид:
Sn = a(1 - qn)/(1 - q)
Где Sn - сумма членов геометрической прогрессии.
Теперь, когда у нас есть формула, мы можем использовать ее для вычисления суммы членов геометрической прогрессии. Зная начальный член, знаменатель и количество членов, мы можем легко найти ответ и лучше понять, как работает геометрическая прогрессия. Практика в вычислении суммы позволяет нам улучшить наши навыки в использовании этой формулы и решении связанных задач.
Вопрос-ответ

Как определить геометрическую прогрессию последовательности?
Для определения геометрической прогрессии последовательности необходимо проверить, что отношение каждого последующего члена к предыдущему всегда одинаково. Если разность между этими отношениями равна постоянной величине, то последовательность является геометрической прогрессией.
Какие методы существуют для определения геометрической прогрессии последовательности?
Для определения геометрической прогрессии можно использовать несколько методов. Один из них - вычисление отношения каждого последующего члена к предыдущему и проверка равенства этих отношений между собой. Также можно воспользоваться формулой для общего члена геометрической прогрессии и проверить, выполняется ли она для всех членов последовательности.
Каким образом можно использовать геометрическую прогрессию в математике или физике?
Геометрическая прогрессия широко используется в математике и физике. Она позволяет предсказывать значения последующих членов последовательности, если известны первый член и ее знаменатель. В математике она применяется для решения различных задач, связанных с числами, формулами и моделями. В физике она использовалась, например, для описания изменения ряда физических величин во времени или пространстве.



