Углы играют важную роль в геометрии, и их тип - тупой или острый, имеет большое значение при решении задач. Если вам нужно определить, является ли данный угол тупым или острым, одним из способов является использование косинуса угла.
Косинус угла - это отношение прилежащей катету к гипотенузе в прямоугольном треугольнике. Если косинус угла больше нуля, то угол острый; если косинус меньше нуля, то угол тупой. Когда косинус равен нулю, угол прямой.
Используя этот простой метод определения угла, можно с легкостью определить, какой тип угла перед вами и продолжить решение задач или конструирование фигур.
Что такое тупой угол?

Определение угла по косинусу
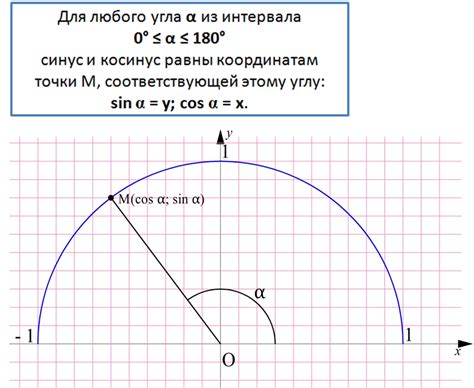
Для определения угла по его косинусу можно использовать тригонометрические функции и таблицу значений. Процедура определения угла по косинусу может быть выполнена в несколько шагов:
- Найдите значение косинуса угла, используя уравнение косинуса: cos(угол) = значение косинуса.
- Используйте таблицу значений косинуса для нахождения угла, соответствующего заданному значению косинуса.
- Если необходимо, проверьте результат, используя другие тригонометрические функции или методы вычисления угла.
Что такое острый угол?

Геометрический признак острого угла – его острые концы, направленные друг к другу. Острый угол присутствует во многих геометрических фигурах, таких как треугольники, четырехугольники и многоугольники.
Как определить острый угол по косинусу?

Если значение косинуса угла меньше 0 и больше -1, то такой угол будет острым. Для определения острого угла по косинусу можно использовать таблицу значений косинуса и его график. При получении отрицательного значения косинуса угла, можно утверждать, что угол острый.
Как вычислить косинус угла?

Косинус угла можно вычислить с помощью тригонометрических функций. Для этого необходимо знать значение угла в радианах или градусах. Обозначим угол как θ.
Для вычисления косинуса угла в радианах используется формула: cos(θ) = cos(θ), где cos - косинус.
Если угол задан в градусах, его необходимо перевести в радианы. Для этого используется формула: угол в радианах = угол в градусах * π / 180, где π - число пи.
После перевода угла в радианы вычисляем косинус по уже известной формуле.
Формула для вычисления косинуса

Для вычисления косинуса угла α существует специальная формула:
| cos(α) = | adjacent side |
| hypotenuse |
где adjacent side - это прилежащий к α стороне прямоугольного треугольника, а hypotenuse - гипотенуза треугольника.
Определение тупого угла через косинус
| Значение косинуса угла | Вид угла |
|---|---|
| 0 < cos(угол) < 1 | Острый угол |
| cos(угол) = 0 | Прямой угол |
| -1 < cos(угол) < 0 | Тупой угол |
Простые шаги для определения тупого угла
Для определения тупого угла необходимо произвести следующие шаги:
- Выберите две прямые на плоскости.
- Установите точку пересечения прямых.
- Измерьте угол между выбранными прямыми.
- Если измеренный угол больше 90 градусов, то это тупой угол.
Вопрос-ответ

Как определить, является ли угол тупым или острым по значению его косинуса?
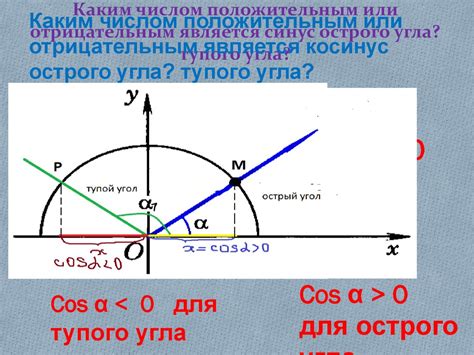
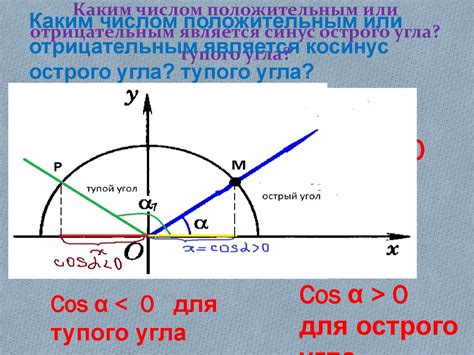
Для определения тупого или острого угла по его косинусу нужно знать, что косинус угла в остроугольном треугольнике всегда положителен, а в тупоугольном - отрицателен. Если косинус угла положителен, то это острый угол. Если косинус отрицателен, то угол тупой.
Можно ли определить тип угла строки из трех точек на плоскости с помощью косинуса?
Да, можно. Для этого, достаточно взять любые два вектора, образованные этими точками, и найти между ними угол. Если косинус этого угла положителен, то угол острый. Если косинус отрицателен, то угол тупой.



