Задача определения высоты треугольника по известной основе является одной из основных в геометрии. Данная информация часто требуется при решении различных задач, в том числе в строительстве, дизайне и архитектуре. Определение высоты треугольника позволяет получить полную картину его формы и параметров, что делает данную задачу важной и интересной.
Для определения высоты треугольника необходимо знать его основу и иметь некоторые геометрические навыки. Высота треугольника - это отрезок, проведенный из вершины треугольника к основанию перпендикулярно ему. Имея эту важную информацию, можно приступить к решению задачи и определению высоты треугольника по известной основе.
Для нахождения высоты треугольника можно использовать различные методы и формулы, в зависимости от доступной информации и типа треугольника. Один из наиболее часто используемых методов - применение теоремы Пифагора или теоремы синусов. Эти методы позволяют определить длину высоты треугольника с высокой точностью и точностью.
Определение высоты треугольника при известной стороне
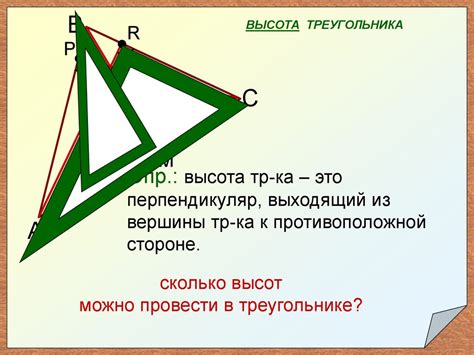
Существует несколько способов определения высоты треугольника при известной стороне, в зависимости от известных параметров и заданных условий. Один из таких способов основан на использовании теоремы Пифагора, применяемой к заданной стороне и высоте. Второй метод включает применение формулы площади треугольника и заданной основы для определения высоты. Третий способ основывается на использовании тригонометрических функций и известных углов треугольника.
Каждый из этих методов имеет свою особенность и применимость в различных ситуациях. Для определения высоты треугольника по известной основе необходимо выбрать наиболее подходящий метод и последовательно провести вычисления. Важно помнить о правильном подборе формул и учете условий задачи для достижения точных и надежных результатов.
Определение высоты треугольника по заданной основе является неотъемлемой частью решения геометрических задач, связанных с треугольниками. Это полезный навык, которым можно овладеть с помощью применения математических концепций и алгоритмов.
Понятие высоты треугольника и его значение
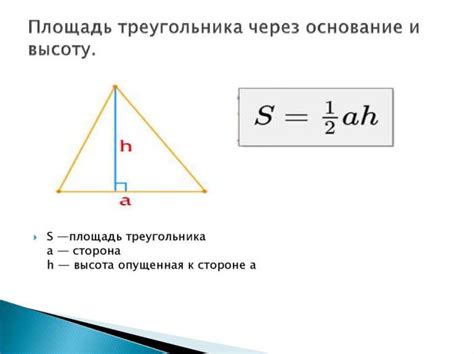
Высота треугольника играет важную роль в геометрии и позволяет решать множество задач. Она помогает определить площадь треугольника, а также связана с понятиями центра тяжести, ортоцентра и медиан.
Знание высоты треугольника позволяет определить его геометрические свойства, а также исследовать его соотношения с другими элементами. Например, зная высоты треугольника, можно вывести формулу для вычисления его площади, которая является основой для множества геометрических и прикладных задач.
Умение определять высоту треугольника по заданной основе дает возможность измерять и анализировать его физические и геометрические характеристики, что важно в таких областях, как строительство, топография, архитектура и другие.
Методы вычисления высоты треугольника по заданной базе
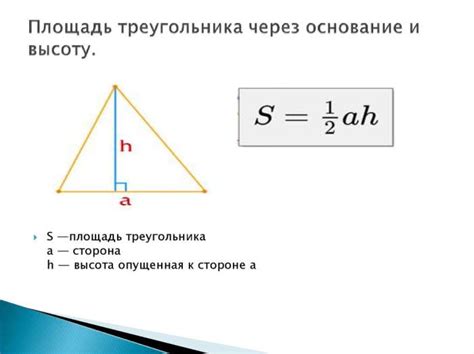
В данном разделе мы рассмотрим различные подходы и алгоритмы, которые позволяют определить высоту треугольника, при известной основе. Без необходимости проводить физические измерения, эти методы позволяют точно вычислить высоту треугольника, что может быть полезно при решении геометрических задач или в практических сферах, требующих знания размеров фигур.
Каждый из методов базируется на математических принципах и знаниях о свойствах треугольников. Мы рассмотрим как классические подходы, основанные на использовании теорем Пифагора и Талеса, так и более продвинутые методы, которые могут использовать геометрические преобразования, векторы или тригонометрию.
Важно отметить, что каждый метод имеет свои преимущества и ограничения, и выбор наиболее подходящего метода зависит от специфики задачи или доступных исходных данных. Кроме того, необходимо учитывать возможную погрешность вычислений, которая может варьироваться в зависимости от используемого метода и точности предоставленных данных.
Цель данного раздела - ознакомить читателя с различными методами определения высоты треугольника по известной основе, а также дать представление о преимуществах и особенностях каждого метода. Это позволит читателю выбрать наиболее подходящий и точный метод для своих задач и получить нужные результаты, не затрачивая лишнего времени и усилий.
Геометрический способ определения выстоты треугольника
Геометрический метод определения высоты треугольника основан на использовании известной основы и свойств треугольников. Для определения высоты можно использовать прямоугольные треугольники, равные треугольники или применить теорему Пифагора и теорему косинусов.
Одним из способов является использование подобных треугольников, основанных на принципе равенства соответствующих углов. Также можно использовать теорему Пифагора для нахождения длины высоты треугольника, зная длины сторон треугольника и его основу.
Геометрический метод позволяет определить высоту треугольника с высокой точностью и без необходимости использования сложных математических вычислений. Он является одним из основных инструментов геометрии и находит применение не только в учебных задачах, но и в практических ситуациях, например, при проектировании строений или измерении расстояний в природе.
Тригонометрический метод нахождения высоты треугольника
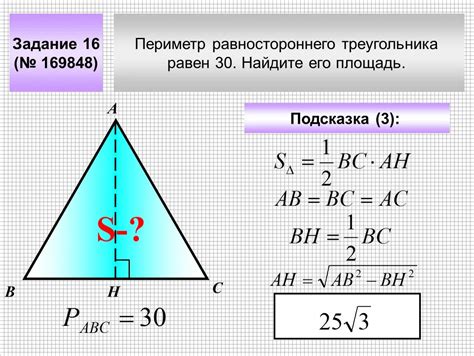
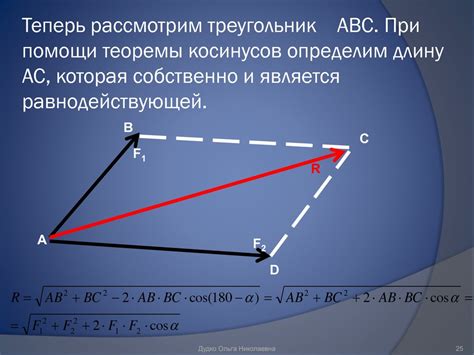
В данном разделе мы рассмотрим тригонометрический метод, который позволит нам определить высоту треугольника на основе известной его стороны. Он основан на использовании тригонометрических функций, а именно синуса и косинуса, для решения задачи нахождения высоты треугольника.
Стартовая точка для использования данного метода – заданная основа треугольника, к которой мы хотим определить высоту. Представим, что мы проводим от заданной основы вертикальную линию, которая пересекает вершину треугольника и образует угол с этой основой. Затем, используя тригонометрические функции и известную длину стороны треугольника, мы сможем определить высоту.
Прейдем к подробному описанию тригонометрического метода определения высоты треугольника. Начальным этапом будет нахождение значения одного из углов треугольника. Для этого мы можем использовать соотношение, демонстрирующее связь синуса угла с отношением противолежащей стороны и основы. Зная значение синуса этого угла и длину основы, мы можем вычислить значение противолежащей стороны и, таким образом, получить высоту треугольника.
Вопрос-ответ

Как определить высоту треугольника?
Для определения высоты треугольника необходимо знать его основу и провести перпендикуляр из вершины треугольника к этой основе. Этот перпендикуляр и будет высотой треугольника.
Зачем нужно измерять высоту треугольника по заданной базе?
Измерение высоты треугольника по заданной базе позволяет нам узнать вертикальное расстояние от основания треугольника до его вершины. Это может быть полезно, например, при решении задач геометрии или в строительстве для определения высоты различных конструкций.
Какие приборы или инструменты нужны для измерения высоты треугольника?
Для измерения высоты треугольника по заданной базе можно использовать различные инструменты, такие как рулетка, линейка или геодезический инструмент под названием нивелир. Важно выбрать инструмент, который позволяет более точно измерить расстояние от основания до вершины треугольника.



