Измерение объема тела или предмета является неотъемлемой частью многих областей науки и инженерии. Определение объема является фундаментальным шагом в решении многих задач, связанных с расчетами и проектированием. В этой статье мы рассмотрим простой и эффективный способ рассчитать объем объекта, исходя из известной площади поперечного сечения.
Площадь поперечного сечения - это мера площади, занимаемой объектом в направлении перпендикулярном к его оси. Она играет важную роль в определении геометрических свойств объекта и может быть измерена с помощью различных инструментов, таких как штангенциркуль или специализированные программы моделирования.
Итак, представьте себе предмет, например, цилиндр с известной площадью поперечного сечения. Чтобы определить его объем, мы должны использовать информацию о площади поперечного сечения и другие связанные параметры. Это позволит нам представить трехмерный объем объекта, который может быть выражен в единицах измерения, таких как кубические миллиметры, кубические сантиметры или даже кубические метры.
Поперечное сечение: основные принципы и применение
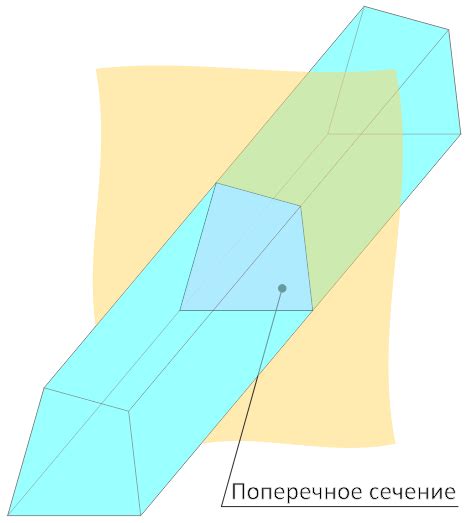
В различных областях науки и техники понятие "поперечное сечение" играет важную роль. Оно представляет собой однопараметрическую характеристику, описывающую геометрические свойства объекта, перпендикулярного оси вращения. Поперечное сечение может быть использовано для описания различных структур и материалов, а также для расчета и анализа их объемов и параметров.
В контексте нашей темы, поперечное сечение позволяет оценить пространственные характеристики объекта, такие как площадь поверхности, периметр, объем и т.д. Это важно при проектировании и строительстве различных конструкций, а также при исследовании материалов и анализе их свойств.
Для расчета объема объекта через площадь поперечного сечения необходимо знать соответствующие формулы и уравнения, которые зависят от геометрической формы сечения. Например, для простой геометрической фигуры, такой как круг, площадь поперечного сечения может быть рассчитана с использованием формулы А=πr^2, где А - площадь, а r - радиус окружности.
Определение объема через площадь поперечного сечения имеет практическое применение в различных отраслях знаний и может быть полезным при разработке и проектировании различных объектов и структур. Дальнейшее изучение данной темы поможет более глубоко понять принципы и методы расчета объемной характеристики объектов на основе их поперечного сечения.
Значение площади поперечного сечения для определения объема

Площадь поперечного сечения - это измерение поверхностной площади, которую занимает сечение объекта, выполненное плоскостью, перпендикулярной к его оси. Она может быть вычислена с использованием различных формул в зависимости от геометрической формы объекта, например круга, прямоугольника, трапеции и других.
Зная площадь поперечного сечения, можно определить объем объекта. Объем - это физическая величина, которая показывает количественное пространство, занимаемое объектом или структурой. Для этого необходимо умножить площадь поперечного сечения на длину объекта либо на высоту структуры.
Понимание значения площади поперечного сечения позволяет производить точные расчеты и измерения, а также определять объемы различных объектов в инженерии, строительстве, архитектуре и других областях. Правильное использование соответствующих формул дает возможность получить точные результаты и учесть особенности геометрии объекта при расчете объема.
Основные подходы для расчета объема на основе площади сечения
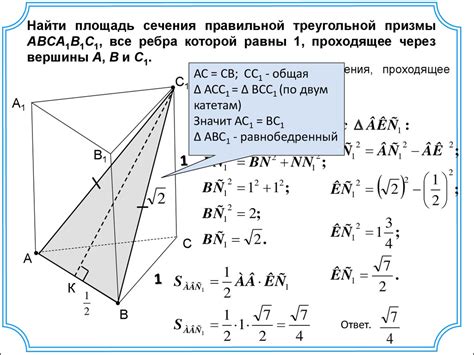
Этот раздел представляет основные методы, которые могут быть использованы для вычисления объема на основе площади поперечного сечения.
Процесс расчета объема требует знания площади поперечного сечения объекта и использования соответствующих формул.
Несмотря на то, что существует множество способов для определения объема, рассмотрим несколько основных и наиболее употребительных методов, которые могут быть применимы в различных сферах.
От физики и строительства до химии и геометрии, точное определение объема является важным аспектом для решения широкого спектра задач и проблем.
Для каждого метода будет представлена соответствующая формула и примеры применения в реальной жизни.
В конце раздела будут рассмотрены преимущества и ограничения каждого метода, а также рекомендации по выбору наиболее подходящего способа для конкретных ситуаций.
Весь представленный материал поможет вам глубже понять процесс расчета объема на основе площади поперечного сечения и применить его в практике.
Метод дискретных сечений

Раздел "Метод дискретных сечений" представляет один из эффективных подходов для определения объема тела на основе площади его поперечного сечения. В данном методе используются техники дискретизации и анализа сечений, позволяющие оценить объем тела с использованием доступных геометрических данных.
Целью метода дискретных сечений является определение объема и формы тела, основываясь на их поперечных сечениях. Он широко применяется в научных и инженерных областях, где требуется точно оценить объем объекта, основываясь на доступной информации о его геометрии.
Для применения метода дискретных сечений необходимо выполнить ряд шагов. Вначале необходимо получить серию поперечных сечений объекта. Для этого можно использовать различные методы, такие как срезание тела на тонкие слои или выполнение серии измерений по всему объему объекта. Затем полученные сечения обрабатываются и анализируются с использованием математических алгоритмов и моделей.
| Шаги метода дискретных сечений: |
|---|
| 1. Получение серии поперечных сечений объекта. |
| 2. Обработка и анализ сечений с использованием математических алгоритмов и моделей. |
| 3. Вычисление площадей сечений и их усреднение. |
| 4. Определение объема объекта на основе усредненных площадей сечений. |
Метод дискретных сечений позволяет оценить объем объекта без необходимости его полного измерения или разрушения. Он является практичным и точным подходом для определения объема на основе площади поперечного сечения, что делает его широко применимым в различных областях науки и техники.
Метод интегрального расчета: определение и принцип работы

Принцип работы метода интегрального расчета заключается в разбиении тела на множество маленьких элементов сечения. Затем, для каждого элемента сечения, находится его площадь способом, соответствующим его форме (например, для круглого сечения используется формула площади круга). Далее, найденные площади элементов сечения интегрируются от начальной до конечной точки тела, чтобы получить общую площадь сечения.
После определения общей площади сечения, объем тела может быть вычислен с использованием формулы, которая связывает площадь сечения и объем. Для простых тел с постоянным сечением, таких как цилиндр или конус, эта формула может быть известна заранее. Однако, для более сложных форм сечений, может потребоваться использование интеграла для вычисления общего объема.
Метод интегрального расчета находит широкое применение в различных областях науки и техники, таких как физика, инженерия и архитектура. Он позволяет точно рассчитывать объем сложных тел, используя только информацию о их поперечном сечении.
Практические примеры расчета объема с использованием площади поперечного сечения

В данном разделе представлены практические примеры, которые иллюстрируют процесс расчета объема с использованием площади поперечного сечения. Этот метод позволяет определить объем тела или структуры, основываясь на известных данных о площади поперечного сечения.
- Пример 1: Расчет объема цилиндра
- Пример 2: Расчет объема прямоугольного параллелепипеда
- Пример 3: Расчет объема конуса
Допустим, у нас есть информация о площади основания цилиндра и его высоте. Для определения объема можно использовать следующую формулу: объем = площадь поперечного сечения * высота. В данном примере мы детально рассмотрим процесс расчета объема цилиндра с использованием данной формулы.
Следуя принципу использования площади поперечного сечения, мы можем рассчитать объем прямоугольного параллелепипеда на основе известной площади его основания и высоты. В этом примере мы разберем процесс расчета объема прямоугольного параллелепипеда и предоставим наглядное объяснение данного метода.
Для расчета объема конуса, мы можем использовать площадь его основания и высоту. Путем применения формулы объема = 1/3 * площадь поперечного сечения * высота, мы можем определить объем данной геометрической фигуры. В этом примере мы более подробно рассмотрим процесс расчета объема конуса и продемонстрируем его на практике.
Практические примеры помогут вам лучше понять и применить метод расчета объема через площадь поперечного сечения. Следуйте инструкциям и используйте соответствующие формулы для точных и надежных результатов.
Рекомендации по применению полученных данных

В данном разделе представлены полезные рекомендации, которые помогут вам эффективно использовать полученные данные о объеме через площадь поперечного сечения в разных сферах деятельности.
- Промышленность
- Определите оптимальный объем для производства исходя из площади поперечного сечения. Это позволит вам эффективно использовать ресурсы и улучшить процесс производства.
- Используйте данные для определения вместимости контейнеров, емкостей или резервуаров, которые будут использоваться в производстве.
- Определите требуемый объем материалов для строительства, учитывая площадь поперечного сечения. Это поможет экономно распределить ресурсы и избежать излишеств или нехватки материалов.
- Используйте данные для планирования размещения строительных конструкций, таких как фундаменты или стены, основываясь на определенном объеме.
- Определите требуемый объем почвы или удобрений для земледелия или создания ландшафтных элементов с учетом площади поперечного сечения. Это поможет обеспечить оптимальные условия для роста растений.
- Используйте данные для расчета объема воды, необходимой для орошения или полива земельных участков, исходя из площади поперечного сечения.
Помните, что полученные данные о объеме через площадь поперечного сечения могут быть полезными во многих областях, где требуется определить объем на основе геометрических характеристик объекта. Внимательно анализируйте данные и применяйте их с умом для достижения наилучших результатов в своей деятельности.
Вопрос-ответ

Как рассчитать объем фигуры, если известна площадь ее поперечного сечения?
Для расчета объема фигуры по площади поперечного сечения нужно учитывать форму фигуры. Если фигура имеет простую геометрическую форму, например, является прямоугольником, кубом или цилиндром, можно использовать соответствующую формулу. Для прямоугольника объем вычисляется как произведение площади поперечного сечения на высоту. Для куба - это степень третья площади одной из его граней. Для цилиндра используется формула V = S * h, где S - площадь поперечного сечения, а h - высота цилиндра. В случае сложных фигур потребуется использовать более сложные методы расчета.
Можно ли рассчитать объем фигуры только зная площадь ее поперечного сечения?
Да, при условии, что известна форма фигуры. Если фигура имеет простую геометрическую форму, то есть у нее прямоугольное, кубическое или цилиндрическое поперечное сечение, то объем можно рассчитать, умножив площадь поперечного сечения на высоту фигуры. Если форма фигуры сложнее, то потребуется применять более сложные методы расчета, например, интегрирование. В случае, если форма фигуры неизвестна, невозможно однозначно рассчитать ее объем только по площади поперечного сечения.
Какие методы расчета объема фигуры по площади поперечного сечения существуют?
Существует несколько методов расчета объема фигуры по площади поперечного сечения, в зависимости от ее формы. Для простых геометрических фигур, таких как прямоугольник, куб или цилиндр, можно использовать соответствующие формулы. Для более сложных фигур, например, неправильных многогранников, понадобится применять методы интегрирования. Для фигур с неизвестной формой существуют также приближенные методы, основанные на анализе статистических данных или создании моделей с учетом определенных предположений.



