Геометрическая прогрессия – это числовая последовательность, в которой каждый последующий член получается умножением предыдущего на определенное число, называемое знаменателем прогрессии.
Одним из важных свойств геометрической прогрессии является то, что она может бесконечно убывать или расти, в зависимости от знака знаменателя.
Докажем, что геометрическая прогрессия, убывающая от 1 до нуля, будет иметь бесконечное количество членов.
Природа геометрической прогрессии
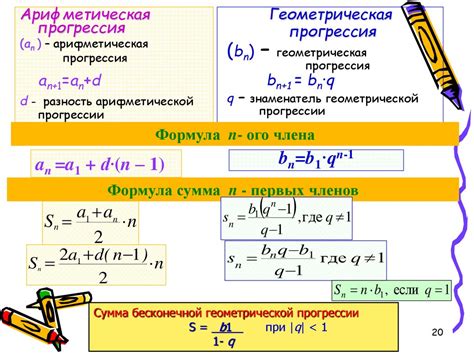
Таким образом, геометрическая прогрессия имеет определенную закономерность и свойственные ей характеристики, отличающие ее от других видов прогрессий.
- Знаменатель прогрессии r не равен нулю, иначе все члены прогрессии будут равны нулю.
- При увеличении номера члена геометрической прогрессии, его значение уменьшается или увеличивается в зависимости от знака знаменателя.
- Бесконечное убывание геометрической прогрессии означает, что каждый последующий член прогрессии будет меньше предыдущего.
Понятие и значения
Значение геометрической прогрессии проявляется в широком спектре областей, таких как математика, физика, экономика и другие. Она позволяет предсказывать развитие процессов, моделировать экономические тенденции, а также решать ряд задач на краткосрочное и долгосрочное планирование.
Основные свойства
- Знаменатель геометрической прогрессии не равен нулю
- При бесконечном убывании знаменатель прогрессии должен быть меньше единицы для того, чтобы геометрическая прогрессия уменьшалась в бесконечности
- Чем меньше модуль знаменателя, тем быстрее прогрессия убывает
Доказательство убывания

Пусть дана геометрическая прогрессия с первым членом a и знаменателем q, где q удовлетворяет условию 0
Докажем это от противного: предположим, что существует такой номер n, что n-ый член прогрессии больше (или равен) (n+1)-го. То есть a*q^(n-1) >= a*q^n. После сокращения a получаем q^(n-1) >= q^n. Разделим обе части на q^(n-1): получим q >= 1, что противоречит условию на q. Значит, утверждение о том, что каждый следующий член прогрессии меньше предыдущего, верно для всех натуральных чисел n.
Метод математической индукции

Применение метода математической индукции требует строгости и внимательности при формулировании базы и шага индукции, чтобы убедиться в корректности доказательства для любого натурального числа.
Вопрос-ответ

Что такое геометрическая прогрессия?
Геометрическая прогрессия - это последовательность чисел, где каждый последующий член получается умножением предыдущего на постоянное число, называемое знаменателем геометрической прогрессии.
Как доказать, что геометрическая прогрессия убывающая?
Для доказательства убывания геометрической прогрессии необходимо установить, что абсолютное значение знаменателя прогрессии меньше 1. Это гарантирует монотонное убывание прогрессии.
Как выявить закономерности в убывающей геометрической прогрессии?
Чтобы выявить закономерности в убывающей геометрической прогрессии, нужно обратить внимание на уменьшающиеся значения членов последовательности с каждым шагом и на отношение соседних членов, которое постоянно и меньше 1.
Почему доказательство бесконечного убывания геометрической прогрессии важно?
Доказательство бесконечного убывания геометрической прогрессии важно, так как позволяет установить, что прогрессия будет убывать бесконечно, пока члены последовательности не станут близки к нулю. Это важно в математике для анализа поведения числовых последовательностей.
Какие методы часто применяют для доказательства бесконечного убывания геометрической прогрессии?
Для доказательства бесконечного убывания геометрической прогрессии часто применяют метод математической индукции или метод анализа знаков, который позволяет установить, что все члены последовательности прогрессии будут меньше нуля при бесконечном продолжении.



