В математике, непрерывная функция на интервале – это функция, для которой значение функции в точке близкой к данной, также близкое к значению функции в этой точке. В контексте математического анализа, доказательство непрерывности функции на интервале является важным шагом для понимания поведения функции в конкретной области.
Доказательство непрерывности функции на интервале обычно включает в себя использование определения непрерывности функции в точке исследуемого интервала. Основное требование для функции быть непрерывной в точке – это то, что предел значения функции в точке равен значению функции в этой точке.
Определение непрерывности функции

Для того чтобы функция была непрерывной на интервале, необходимо, чтобы она сохраняла свои значения на этом интервале без разрывов и рывков. Формально, функция f(x) называется непрерывной в точке c, если предел функции в этой точке существует и равен значению функции в этой точке: f(c) = lim x->c f(x). Если функция непрерывна в каждой точке интервала [a, b], то она непрерывна на этом интервале в целом.
| Тип непрерывности | Описание |
|---|---|
| Непрерывность функции слева | Функция непрерывна в точке с, если предел функции существует с левой стороны от точки с и равен значению функции в точке с. |
| Непрерывность функции справа | Функция непрерывна в точке с, если предел функции существует с правой стороны от точки с и равен значению функции в точке с. |
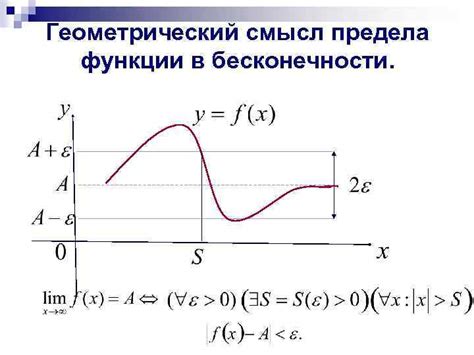
Связь с понятием предела
Типы точек непрерывности
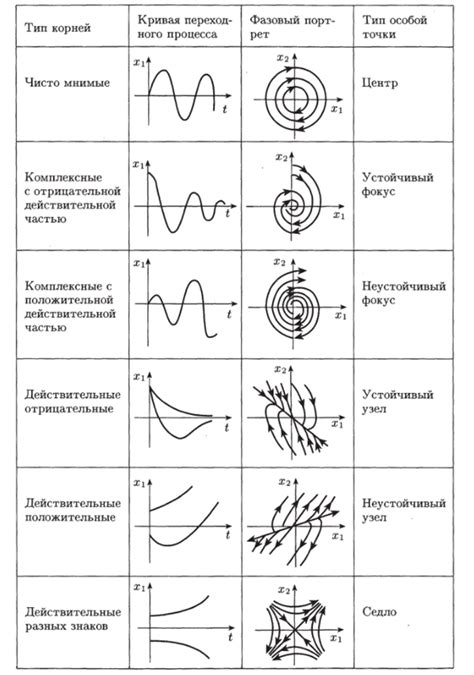
В зависимости от поведения функции в точке, выделяют несколько типов точек непрерывности:
| Тип точки | Описание |
|---|---|
| Непрерывная точка | Функция непрерывна в данной точке и имеет конечное значение в этой точке. |
| Разрыв первого рода | Функция имеет разрыв в данной точке, но существуют конечные односторонние пределы функции с обеих сторон от точки. |
| Разрыв второго рода | Функция имеет разрыв в данной точке и не имеет пределов с обеих сторон от точки. |
Понимание этих типов точек непрерывности помогает более глубоко изучать поведение функций на интервалах.
Разрывы первого рода

Разрывы первого рода функций на интервале возникают, когда функция имеет точку нарушения непрерывности. Такие точки приравнивают к разрывам, которые возникают из-за различий между левосторонним и правосторонним пределами функции в этой точке. Иными словами, функция может быть непрерывной слева или справа от разрыва, но не в самой точке разрыва.
Разрывы первого рода могут быть классифицированы на разрывы типа "прыжок" (quasicontinuity) и разрывы типа "луч" (asymptotic discontinuity). Разрыв "прыжок" характеризуется значительным изменением функции в точке разрыва, тогда как разрыв "луч" проявляется в бесконечном увеличении функции до разрыва или после него.
Для доказательства непрерывности функции на интервале с разрывами первого рода необходимо учитывать особенности левостороннего и правостороннего поведения функции вблизи точки разрыва и обосновать ее непрерывность с учетом типа разрыва.
Разрывы второго рода

Данный тип разрывов является более сложным и требует особого рассмотрения при анализе непрерывности функции на интервале. Для их выявления необходимо провести детальный анализ асимптотического поведения функции в окрестности точки разрыва.
Теорема о сохранении непрерывности
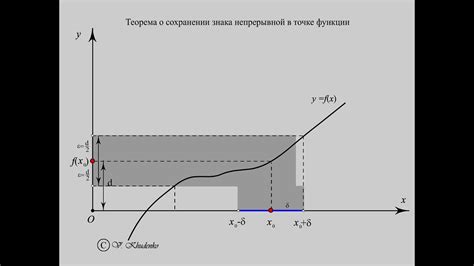
Если функция \( f(x) \) непрерывна на интервале \([a, b]\) и монотонна, то она сохраняет непрерывность на этом интервале.
Другими словами, если функция непрерывна на интервале и не меняет свой характер (не имеет разрывов), то она остается непрерывной на этом интервале.
При выполнении определенных условий

Важно отметить, что для доказательства непрерывности функции на интервале необходимо соблюдать определенные условия.
Среди основных условий, которые должны быть выполнены, можно выделить:
- Функция должна быть определена на интервале: чтобы функция была непрерывной на интервале, она должна быть определена на всем этом интервале. Необходимо проверить наличие разрывов и точек разрыва в области определения функции.
- Ограниченность функции: важно, чтобы функция была ограничена на интервале для того, чтобы можно было гарантировать непрерывность.
- Отсутствие разрывов: функция не должна иметь разрывов первого рода на интервале. Разрывы первого рода могут нарушить непрерывность функции.
При соблюдении данных условий, можно доказать непрерывность функции на интервале и использовать соответствующие методы для данной задачи.
Методы доказательства непрерывности

Существует несколько основных методов для доказательства непрерывности функции на интервале:
1. Доказательство с помощью определения непрерывности: По определению непрерывности функции в точке, необходимо показать, что при близких к данной точке значениях аргумента, значения функции также близки.
2. Доказательство с использованием предельных переходов: Для доказательства непрерывности функции на интервале можно использовать предельные переходы – пределы функции при стремлении аргумента к заданной точке.
3. Доказательство с помощью теоремы о связи между непрерывностью и предельными переходами: Используя свойство непрерывности функции, можно утверждать, что функция непрерывна на интервале, если предел функции существует в каждой точке интервала.
Вопрос-ответ

Как можно доказать непрерывность функции на интервале?
Для доказательства непрерывности функции на интервале обычно используют теорему о непрерывности композиции функций. Также можно применить метод последовательностей, доказывая непрерывность функции на интервале через пределы последовательностей. Критерием непрерывности является существование конечного предела функции в каждой точке интервала.
Какие условия должны быть выполнены для доказательства непрерывности функции?
Для доказательства непрерывности функции на интервале необходимо, чтобы функция была определена на данном интервале, имела конечные значения в каждой точке интервала и не имела резких перепадов. Также важно проверить выполнение определения непрерывности в каждой точке интервала для общего вывода о непрерывности на всем интервале.
Могут ли быть исключения, когда функция кажется непрерывной, но на самом деле не является?
Да, иногда функция может казаться непрерывной на интервале, но на самом деле иметь разрывы или другие особенности, которые нарушают непрерывность. Например, у функции могут быть точки разрыва первого рода или второго рода, что делает ее непрерывность на интервале спорной. Поэтому важно проводить тщательный анализ функции и выполнение условий непрерывности.
Какой графический признак может указывать на непрерывность функции на интервале?
Графический признак непрерывности функции на интервале может проявляться в отсутствии резких "скачков" графика, плавности изменения функции в пределах интервала и отсутствии изоляированных точек разрыва. Если график функции имеет непрерывную кривую без резких перепадов, большинство значений в пределах интервала сходятся к одной точке, это может свидетельствовать о непрерывности функции на данном интервале.



