Давайте представим себе захватывающий мир геометрии, где прямые линии и углы становятся нашими верными помощниками в поиске истины. Сегодня мы отправимся в путешествие по миру кубов и узнаем, как найти длину всех его ребер.
Что такое куб? Куб – это трехмерный объект, в котором все его шесть граней состоят из квадратных плоскостей. О, как заманчиво и гармонично звучит это определение! Но не будем тратить время на лишние слова и приступим к делу, чтобы воочию увидеть и почувствовать математическую гармонию, воплощенную в кубе!
Наша задача заключается в определении длины всех ребер куба. Что такое ребро? Ребро – это отрезок, соединяющий две вершины. Когда мы найдем длину каждого ребра, то сможем полностью описать геометрические особенности этого фантастического объекта. Готовы отправиться в эту увлекательную математическую экспедицию? Тогда давайте приступим!
Свойства и описание куба
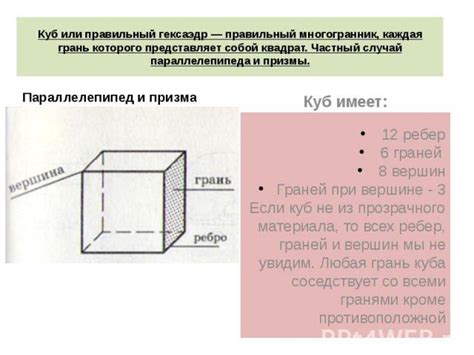
Одно из основных свойств куба - его регулярная форма и одинаковые стороны. Во всех трех измерениях (длина, ширина и высота) куб имеет одинаковые размеры и равные ребра. За счет этой симметричности куб часто используется для изготовления объектов, требующих точности и стабильности.
Куб имеет шесть одинаковых граней, каждая из которых представляет собой квадрат. Грани куба параллельны друг другу и ограничивают внутреннее пространство. Каждая грань куба встречается с другими гранями под прямыми углами.
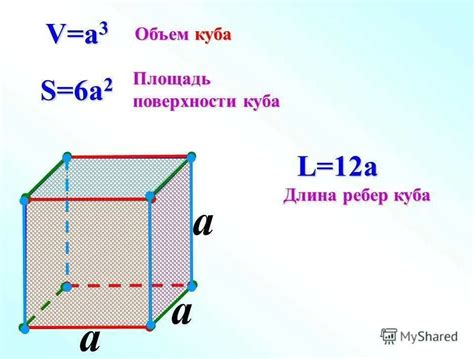
Важным свойством куба является его объем. Объем куба можно вычислить, возведя в квадрат длину его ребра. Куб имеет также площадь поверхности, которая является суммой площадей всех его граней. Площадь поверхности куба можно найти, умножив длину ребра на 4.
Таким образом, куб - это геометрическое тело с регулярной формой, одинаковыми ребрами и гранями, встречающимися под прямым углом. Познакомившись с его основными свойствами, мы можем глубже понять и описать эту геометрическую фигуру.
Зачем нам нужно знать размеры сторон куба
| Область применения | Значимость знания |
|---|---|
| Архитектура и строительство | Зная размеры сторон куба, мы можем точно расчитать объемы конструкций, определить необходимые материалы для строительства и ремонта. |
| Производство и дизайн | Используя длины ребер куба, мы можем создавать модели и прототипы различных предметов и устройств, таких как мебель, игрушки, электроника и многое другое. |
| Расчеты в физике и технике | При решении задач в физике и технике, часто требуется знать объемы, площади поверхности или размеры сторон куба, чтобы проводить правильные и точные расчеты. |
| Игры и головоломки | Зная размеры сторон куба, мы можем легко собирать различные головоломки и игрушки, такие как "Рубикова кубика", и наслаждаться увлекательным процессом. |
Таким образом, знание длин сторон куба дает нам возможность более глубокого и точного понимания математических и геометрических принципов, а также полезно в решении повседневных задач и применении на практике в различных областях. Поэтому необходимо уделять внимание изучению этой величины и пониманию ее значимости.
Определение длины одного сдвига куба
В этом разделе мы рассмотрим простой и понятный способ вычисления размера одного сдвига куба. Мы узнаем, как определить длину стороны куба без использования сложных формул и математических концепций.
Одной из важных характеристик куба является его длина стороны, которая показывает нам, насколько "длинными" являются ребра этой геометрической фигуры. Длина одного сдвига куба определяет равенство длины всех его ребер.
В дальнейшем мы рассмотрим простой метод, который поможет нам найти длину одного ребра куба. Мы будем использовать основные геометрические понятия и логику, чтобы достичь нашей цели. Без использования сложных математических формул и терминологии, мы сможем легко понять принцип и применить его на практике.
Давайте начнем наше знакомство с кубом и узнаем, как найти длину одного ребра с помощью простых шагов и легко доступных средств. Это будет интересно и полезно для учеников пятого класса, которые только начинают изучать геометрию и математику. Приступим!
Сущность ребра куба
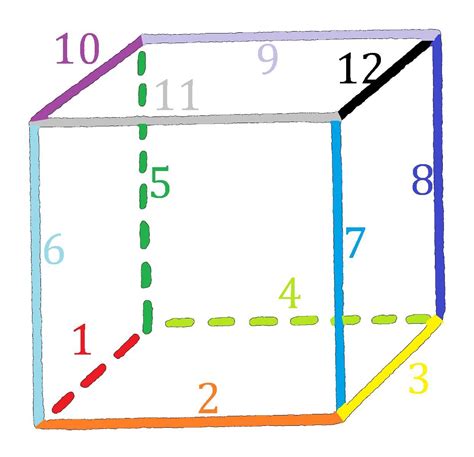
Для учеников 5 класса изучение ребер куба является частью курса геометрии, который предоставляет возможность познакомиться с основными понятиями и принципами этой науки. При изучении ребер куба, дети учатся определять и измерять их длину, различать основные характеристики и взаимосвязи между ними. Процесс изучения способствует развитию навыков анализа, логического мышления, визуального восприятия и математической интуиции.
| Ребро куба | Описание |
|---|---|
| 1. Ребро | Первая сторона куба, соединяющая две вершины и определяющая его длину. |
| 2. Ребро | Вторая сторона куба, соединяющая другие две вершины и имеющая свою уникальную длину. |
| 3. Ребро | Третья сторона куба, также соединяющая две вершины и имеющая свою индивидуальную длину. |
| 4. Ребро | Четвертая сторона куба, соединяющая оставшиеся две вершины и обладающая своей характерной длиной. |
| 5. Ребро | Пятая сторона куба, соединяющая остальные две вершины и имеющая свою уникальную протяженность. |
| 6. Ребро | Шестая и последняя сторона куба, соединяющая остающиеся две вершины и имеющая свою отдельную длину. |
Формула для определения размера стороны
В данном разделе мы поговорим о способе определения длины стороны куба без необходимости измерять каждое ребро отдельно. Благодаря использованию специальной формулы, мы сможем быстро и точно вычислить размер стороны куба.
Формула для вычисления длины ребра куба - это математическое выражение, которое позволяет нам определить размер стороны куба на основе других известных данных. Она основана на связи между стороной куба и его объемом или площадью поверхности.
Применение этой формулы поможет нам с легкостью определить длину стороны куба и понять, какие известные значения необходимо использовать в расчете. Также стоит обратить внимание на то, что найденная длина стороны будет иметь такую же единицу измерения, как и использованные изначально данные.
Вопрос-ответ

Как найти длину всех ребер куба для учеников 5 класса?
Для того чтобы найти длину всех ребер куба, необходимо знать одну из его сторон. Зная длину одной стороны, мы можем умножить ее на 12, так как куб имеет 6 граней, и каждая грань состоит из двух ребер. Таким образом, длина всех ребер куба равна удвоенной длине одной из его сторон. Например, если длина одной стороны куба равна 5 см, то длина всех его ребер будет 10 см.
Какая формула позволяет найти длину всех ребер куба?
Формула для нахождения длины всех ребер куба не нужна. Длина всех ребер куба равна удвоенной длине одной из его сторон. Другими словами, если длина одной стороны куба равна S, то длина всех его ребер будет 2S.
Как можно определить длину одной стороны куба, зная длину одного из его ребер?
Длина одной стороны куба равна длине одного из его ребер. В отличие от прямоугольников и других многогранников, все ребра куба равны между собой. Таким образом, если известна длина одного из ребер куба, то это и будет длина одной из его сторон.
Как можно найти длину одного из ребер куба, если известна его площадь грани?
Нельзя однозначно найти длину одного из ребер куба, используя только площадь его грани. Для определения длины ребра куба требуется знать одну из его сторон или объем. Длина ребра куба не зависит от площади его грани.
Как можно узнать объем куба, зная длину его ребра?
Объем куба можно найти, возведя длину его ребра в куб. То есть, объем куба равен третьей степени длины его ребра. Например, если длина ребра куба равна 3 см, то его объем будет равен 27 см³.



