Сокращение дробей с буквами – это процесс упрощения математических выражений, включающих переменные. В задачах, где числа заменены буквами, необходимо сокращать дроби, чтобы получить более удобные и простые выражения. Этот процесс является важным шагом в решении уравнений и других математических задач.
Для успешного сокращения дробей с буквами следует придерживаться определенных правил. Важно уметь выносить общие множители за скобки, упрощать числитель и знаменатель, а также обратить внимание на степени переменных. Следует действовать осторожно и внимательно, чтобы не допустить ошибок в вычислениях.
В данной статье мы рассмотрим важные правила сокращения дробей с буквами и предоставим примеры, которые помогут четко понять процесс упрощения и применить его в практике.
Как сократить дробь с буквами?

Пример:
Дана дробь с буквами: $\frac{3x^2y^3}{6xy}$. Для сокращения найдем общие множители в числителе и знаменателе:
Числитель: 3, x в степени 2, y в степени 3.
Знаменатель: 6, x, y.
Находим общие множители: 3, x, y.
Делим числитель и знаменатель на наибольший общий множитель:
Итак, $\frac{3x^2y^3}{6xy} = \frac{3x^2y^3}{3 \cdot 2 \cdot x \cdot y} = \frac{x(y^2)}{2}$.
Основные правила сокращения

1. Общие множители: Дробь с буквенными выражениями можно сократить, если в числителе и знаменателе есть общий множитель. Например, если есть дробь a^2b^3 / ab^2, то она может быть сокращена до ab.
2. Буквенные выражения: Дроби с буквенными выражениями должны содержать одни и те же буквенные переменные, чтобы быть сокращенными. Например, дробь a^2b^3 / ab^2 не может быть сокращена, потому что переменные a и b не совпадают полностью.
3. Сложные выражения: В случае сложных выражений, необходимо аккуратно упростить дробь, подчеркнуть общие множители и только потом сокращать.
Примеры сокращения дробей

Допустим, у нас есть дробь a/b:
| Дробь | Сокращенный вид |
| a/b | не имеет общих делителей больше единицы |
| 6x/12 | x/2 |
| 15a^2b/45ab^2 | a/3b |
Сокращение дробей с буквами: практика

| Пример | Исходная дробь | Сокращенная дробь |
|---|---|---|
| 1. | 2x/4 | x/2 |
| 2. | 3a^2b/6ab | a/2b |
| 3. | 4m^2n/8mn | m/2 |
В практике сокращения дробей с буквами, необходимо выделить общие множители и сокращать их как числовые коэффициенты. Результат полученных дробей зависит от принятого правила исключения общих множителей.
Практические упражнения по сокращению дробей

Приведите дробь к наименьшему знаменателю:
- Сократите дробь \( \frac{4x^2}{8xy} \)
- Упростите \( \frac{15ab^3}{30a^2b^2} \)
Решения:
- Дробь \( \frac{4x^2}{8xy} \) можно сократить, разделив числитель и знаменатель на их НОД, получаем \( \frac{4x}{8y} = \frac{1}{2y} \)
- Дробь \( \frac{15ab^3}{30a^2b^2} \) упрощается до \( \frac{1}{2ab} \)
Сокращение дробей с буквенными выражениями

Для более сложных выражений с несколькими переменными также нужно идентифицировать общие множители и делители и провести их сокращение. Важно помнить, что при сокращении дробей с буквенными выражениями нужно быть внимательным и аккуратно работать с переменными и их степенями.
| Пример | Исходная дробь | Сокращенная дробь |
| 1 | (3x^2y) / (6xy) | 1/2 |
| 2 | (4a^3b) / (8ab^2) | 1/2a |
Пошаговая инструкция по сокращению дробей
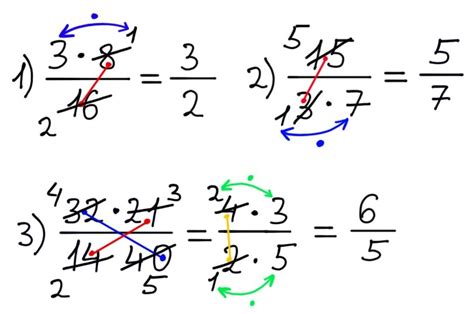
Для сокращения дробей с буквами следуйте этой инструкции:
| 1 | Разложите числитель и знаменатель на простые множители. |
| 2 | Упростите дробь, сократив все общие множители числителя и знаменателя. |
| 3 | Дробь считается сокращенной, если не существует общих простых множителей числителя и знаменателя. |
Советы по минимизации числителя и знаменателя

При сокращении дробей с буквами, следует учитывать ряд основных правил, которые помогут минимизировать числитель и знаменатель:
- Выделить общие множители и разложить выражения на простые множители;
- Использовать свойства степеней для упрощения выражений;
- В случае наличия корней, стараться вынести подобные из-под них;
- Избегать лишних операций с буквами и числами, упрощая выражения относительно знаков и степеней;
- Запомнить основные формулы и правила сокращения дробей с буквами.
Соблюдение этих советов поможет эффективно сокращать дроби с буквенными выражениями, делая математические операции более легкими и понятными.
Вопрос-ответ

Какие правила сокращения дробей с буквами?
Сокращение дробей с буквами происходит путем нахождения общих множителей в числителе и знаменателе и их сокращения. При этом нужно помнить, что при сокращении дробей с буквами можно сокращать только множители, а не отдельные буквы.
Какую дробь с буквами можно сократить?
Дроби с буквами можно сокращать, если в числителе и знаменателе есть общие множители. Например, если в числителе есть буква "а" во второй степени, а в знаменателе - в первой степени, то эти две буквы "а" можно сократить.
Какие ошибки чаще всего допускают при сокращении дробей с буквами?
Одной из частых ошибок при сокращении дробей с буквами является сокращение букв, а не их степеней. Также ошибкой будет сокращение различных букв, например "а" и "b", если они не образуют общий множитель. Необходимо внимательно просматривать каждый множитель.
Можете привести пример сокращения дроби с буквами?
Конечно! Представим, что у нас есть дробь (3a^2bc)/(6ab^3c). Путем нахождения общего множителя в числителе и знаменателе можно сократить на "a" и "c", получив результат 1/(2b^3).
Какой смысл имеет сокращение дробей с буквами?
Сокращение дробей с буквами помогает упростить выражения, делая их более компактными и удобными для дальнейших вычислений. Это позволяет лучше понять структуру и взаимосвязи элементов алгебраических выражений.



