Остроугольный треугольник – это треугольник, у которого угол между любыми двумя сторонами является острым (меньше 90 градусов). Для определения остроугольного треугольника по сторонам можно воспользоваться несколькими правилами.
Проверьте, выполняется ли неравенство треугольника для заданных сторон: сумма двух сторон всегда должна быть больше третьей стороны. Если это условие выполняется, то треугольник с указанными сторонами существует.
Метод Пифагора для определения остроугольного треугольника

Свойства остроугольных треугольников
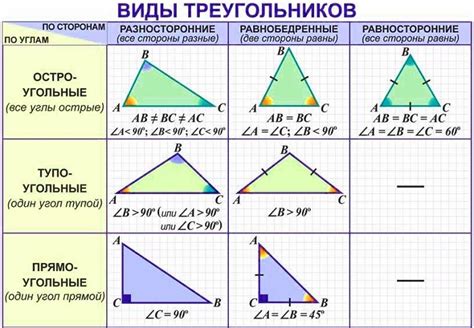
- Сумма углов остроугольного треугольника равна 180 градусов.
- В остроугольном треугольнике длины всех сторон положительны и удовлетворяют неравенству треугольника: сумма длин двух сторон всегда больше длины третьей стороны.
- Остроугольный треугольник всегда является выпуклым (все вершины направлены в одну сторону).
Свойства остроугольных треугольников могут быть использованы при решении геометрических задач и доказательстве различных утверждений о треугольниках.
Сумма углов в остроугольном треугольнике
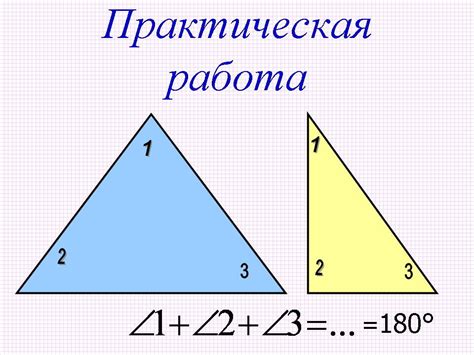
Сумма углов в любом треугольнике всегда равна 180 градусов. В случае остроугольного треугольника сумма трех его углов равна 180 градусов.
Для определения составляющих углов остроугольного треугольника можно использовать теорему о сумме углов в треугольнике: сумма всех углов треугольника равна 180 градусов.
Равенство сторон в остроугольном треугольнике
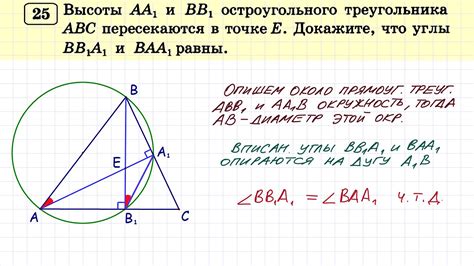
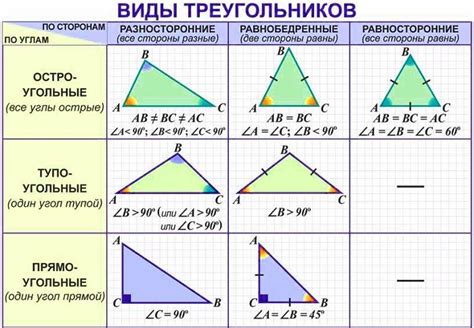
Различия между остроугольным и тупоугольным треугольниками
| Параметр | Остроугольный треугольник | Тупоугольный треугольник |
|---|---|---|
| Величина углов | Все углы остроугольного треугольника меньше 90 градусов. | В тупоугольном треугольнике есть хотя бы один угол больше 90 градусов. |
| Свойства сторон | Все стороны остроугольного треугольника меньше гипотенузы. | В тупоугольном треугольнике существует сторона, которая больше гипотенузы. |
| Связь с углом наклона | Остроугольный треугольник чаще всего связан с углами наклона менее 45 градусов. | Тупоугольный треугольник связан с углами наклона более 45 градусов. |
Условие существования остроугольного треугольника
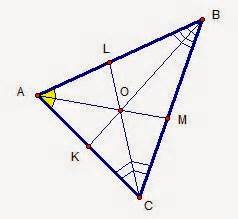
Остроугольный треугольник существует, если условие каждой стороны, больше чем разность двух остальных сторон.
То есть: для треугольника со сторонами a, b и c, где a c^2.
Вычисление углов в остроугольном треугольнике

Для вычисления углов в остроугольном треугольнике можно воспользоваться теоремой косинусов и тригонометрическими функциями.
Углы можно вычислить следующим образом:
- Угол A: Используя теорему косинусов, вычисляем косинус угла A по формуле: cos(A) = (b^2 + c^2 - a^2) / 2bc, где a, b, c - длины сторон треугольника. Затем находим значение угла A по формуле: A = arccos(cos(A)).
- Угол B: Угол B можно найти, используя угол A и тот факт, что сумма углов треугольника равна 180 градусов: B = 180 - A - C.
- Угол C: Угол C можно найти, используя углы A и B: C = 180 - A - B.
Проверка условия остроугольности треугольника
- Сумма квадратов двух меньших сторон треугольника должна быть больше квадрата самой большой стороны.
- Другими словами, для сторон треугольника a, b, c условие остроугольности можно записать как: a^2 + b^2 > c^2, b^2 + c^2 > a^2, a^2 + c^2 > b^2.
Примеры решения задач на остроугольные треугольники
Рассмотрим задачу: в остроугольном треугольнике известны стороны a = 5, b = 12 и c = 13. Найдем углы треугольника по формулам косинусов.
| Сторона | Длина |
|---|---|
| a | 5 |
| b | 12 |
| c | 13 |
Первым шагом найдем угол между сторонами a и b:
cosA = (b^2 + c^2 - a^2) / 2bc
cosA = (12^2 + 13^2 - 5^2) / (2 * 12 * 13) = (144 + 169 - 25) / 312 = 288 / 312 = 0.9231
Угол A = arccos(0.9231) ≈ 22.62°
Аналогично найдем угол B между сторонами a и c:
cosB = (a^2 + c^2 - b^2) / 2ac
cosB = (5^2 + 13^2 - 12^2) / (2 * 5 * 13) = (25 + 169 - 144) / 130 = 50 / 130 = 0.3846
Угол B = arccos(0.3846) ≈ 67.38°
Наконец, угол C между сторонами b и c найдем аналогично:
cosC = (a^2 + b^2 - c^2) / 2ab
cosC = (5^2 + 12^2 - 13^2) / (2 * 5 * 12) = (25 + 144 - 169) / 120 = 0 / 120 = 0
Угол C = arccos(0) = 90°
Таким образом, остроугольный треугольник с сторонами 5, 12 и 13 имеет углы A ≈ 22.62°, B ≈ 67.38° и C = 90°.
Остроугольный треугольник в геометрии
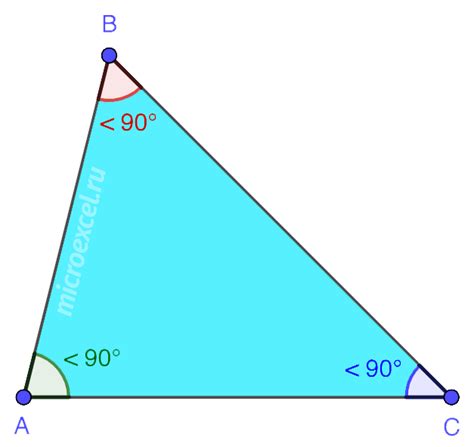
Для определения остроугольного треугольника по сторонам необходимо проверить, что квадрат длины каждой стороны треугольника меньше суммы квадратов длин двух других сторон. Если данное условие выполняется для всех сторон треугольника, то можно утверждать, что он является остроугольным. Этот признак связан с тем, что в остроугольном треугольнике наибольшая сторона меньше суммы двух других сторон, что обеспечивает его острой форму.
Вопрос-ответ

Как определить остроугольный треугольник по сторонам?
Остроугольный треугольник – это треугольник, у которого каждый угол меньше 90 градусов. Для определения остроугольного треугольника по сторонам можно воспользоваться теоремой Пифагора и неравенством треугольника. Если сумма квадратов катетов (меньших сторон) больше квадрата гипотенузы (большей стороны), то треугольник остроугольный. Например, если стороны треугольника равны 3, 4 и 5, то 3^2 + 4^2 = 9 + 16 = 25, что менее, чем 5^2, следовательно, это остроугольный треугольник.
Какие свойства остроугольного треугольника?
Остроугольный треугольник обладает следующими свойствами: 1) Все углы треугольника меньше 90 градусов. 2) Высоты треугольника, опущенные из вершин, пересекаются внутри треугольника. 3) Внутренние углы остроугольного треугольника суммируются до 180 градусов. 4) Сумма квадратов катетов (малых сторон) остроугольного прямоугольного треугольника равна квадрату гипотенузы (большей стороны).
Есть ли другие способы определить остроугольный треугольник?
Кроме вышеописанного способа с использованием теоремы Пифагора, остроугольный треугольник можно определить с помощью синусов углов треугольника. Если синусы всех углов треугольника положительны, то треугольник остроугольный. Также можно использовать неравенство треугольника, если сумма двух сторон треугольника больше третьей стороны, то треугольник остроугольный.
Может ли равнобедренный треугольник быть остроугольным?
Да, равнобедренный треугольник может быть остроугольным. В равнобедренном треугольнике два угла при основании равны между собой, и если эти углы остроугольные, то и весь треугольник будет остроугольным. Например, равнобедренный треугольник со сторонами 3, 3, 4 будет остроугольным, так как два угла при основании будут острыми.



