Умножение двух чисел – это одна из основных арифметических операций, которая позволяет найти произведение чисел. Но каково значение этой операции, когда речь идет о физических величинах, таких как длина и высота?
Длина и высота – это параметры, которые характеризуют геометрические фигуры, пространственные объекты или строения. Умножение длины на высоту может иметь различный смысл в разных контекстах, например, при вычислении площади прямоугольника или объема параллелепипеда.
Познакомьтесь с интересными примерами и задачами, где умножение длины на высоту играет важную роль и помогает нам понять мир вокруг нас с математической точки зрения.
Размер фигуры
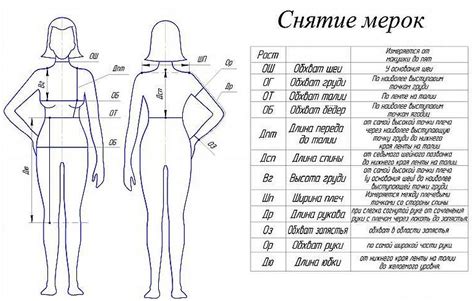
Расчет размера фигуры путем умножения длины на высоту применяется при работе с прямоугольными и параллелограммами. Этот метод позволяет определить площадь фигуры и оценить ее размер в двух измерениях.
Учтите, что умножение длины на высоту может быть не единственным способом расчета размера фигуры, в зависимости от формы и геометрических характеристик объекта.
Значение длины и высоты
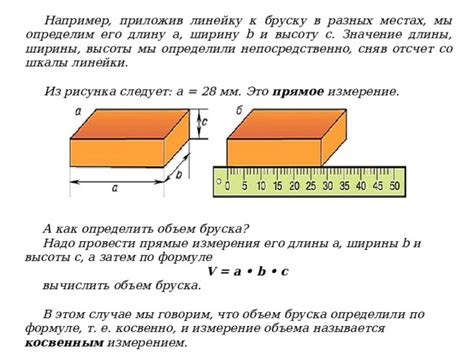
Формула площади
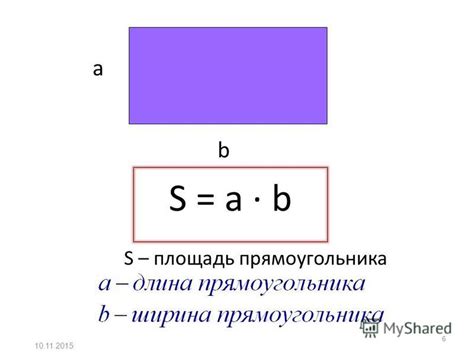
Площадь прямоугольника можно вычислить как произведение его длины на ширину. Эта формула применима и для других фигур.
Для прямоугольника: S = a * b, где S - площадь, a - длина, b - ширина.
Для треугольника: S = 0.5 * a * h, где h - высота, опущенная на основание треугольника, а a - длина этого основания.
Для круга: S = π * r^2, где r - радиус круга, π - число пи, примерно равное 3.14.
Геометрический смысл

Зависимость параметров
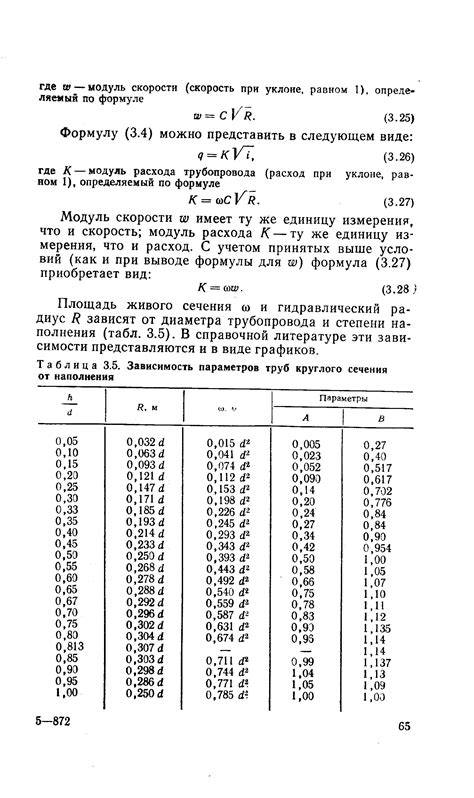
Умножение длины на высоту играет важную роль при решении различных задач в математике и науке. Зависимость этих параметров может влиять на результаты расчетов и предсказаний. Например, в геометрии умножение длины на высоту приводит к нахождению площади многоугольника или треугольника.
В физике зависимость параметров длины и высоты может влиять на поверхность тела, его объем или геометрическую форму. Умножение длины на высоту в экономике может привести к рассмотрению площадей графиков или таблиц, что поможет увидеть взаимосвязь между двумя величинами.
Таким образом, умножение длины на высоту позволяет изучать и анализировать зависимость параметров в различных научных областях, что значительно облегчает понимание и принятие решений на практике.
Примеры расчетов

Допустим, у нас есть прямоугольный параллелепипед со следующими параметрами:
- Длина: 6 см
- Ширина: 3 см
- Высота: 4 см
Чтобы найти объем этого параллелепипеда, мы можем умножить его длину на высоту: 6 см * 4 см = 24 см³.
Таким образом, объем прямоугольного параллелепипеда равен 24 кубическим сантиметрам.
Практическое применение

Умножение длины на высоту находит свое практическое применение в различных областях, таких как геометрия и физика. Например, при расчете площади прямоугольника, необходимо умножить длину на высоту. В архитектуре и строительстве также часто используется этот принцип для расчета объема помещения или площади стен.
Важно отметить, что умножение длины на высоту также может быть полезным при расчетах площадей тел в трехмерном пространстве, например, объемов параллелепипедов или при расчете объема жидкости в сосуде.
Вопрос-ответ

Какие результаты можно получить, умножив длину на высоту?
Умножение длины на высоту применяется для расчета площади различных фигур. Например, площадь прямоугольника равна произведению его длины на высоту. Также в геометрии умножение длины на высоту может использоваться для нахождения объема некоторых тел, если известна третья размерность.
Какие свойства имеют умножение длины на высоту?
Применение умножения длины на высоту может помочь определить площадь фигуры. Например, для прямоугольника площадь равна произведению длины на высоту. Также умножение длины на высоту широко используется в геометрии для решения задач по нахождению объема тел и площади поверхности.



