Вычисление тригонометрических функций – важный аспект математики, который находит применение в различных областях науки и техники. Одной из таких функций является тангенс угла. Иногда бывает, что известны лишь синус и косинус угла, и необходимо определить значение тангенса.
Существует простая формула для вычисления тангенса угла по синусу и косинусу: тангенс угла равен отношению синуса к косинусу. Таким образом, чтобы найти тангенс угла, нужно разделить значение синуса угла на значение косинуса угла.
Давайте рассмотрим пример: если известно, что синус угла равен 0.6, а косинус угла равен 0.8, то для нахождения тангенса угла нам достаточно разделить 0.6 на 0.8. Таким образом, тангенс угла будет равен 0.75. Просто, правда?
Как найти тангенс угла?

Для того чтобы найти тангенс угла, нужно воспользоваться формулой: тангенс угла равен отношению синуса угла к косинусу угла.
То есть, если известны значения синуса (sin) и косинуса (cos) угла, то тангенс (tan) угла можно найти по формуле:
tan(угла) = sin(угла) / cos(угла)
Пример:
Пусть sin(угла) = 0.8 и cos(угла) = 0.6
Тогда тангенс угла будет:
tan(угла) = 0.8 / 0.6 = 1.33
Формула для расчета

Для вычисления тангенса угла по заданным значениям синуса и косинуса используется следующая формула:
| tan(α) = sin(α) / cos(α) |
Где:
- tan(α) - значение тангенса угла α
- sin(α) - значение синуса угла α
- cos(α) - значение косинуса угла α
Применяя данную формулу, можно легко вычислить значение тангенса угла при известных синусе и косинусе.
Пример 1: Нахождение тангенса
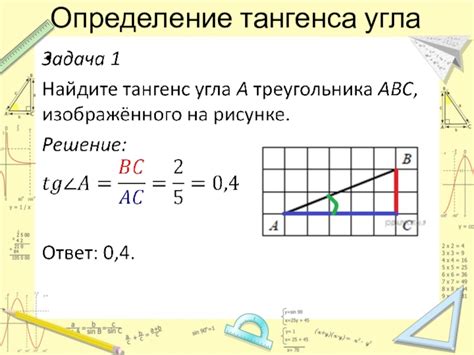
Пусть угол α таков, что sin(α) = 3/5 и cos(α) = 4/5.
Тогда тангенс α можно найти по формуле:
tan(α) = sin(α)/cos(α) = (3/5) / (4/5) = 3/4.
Таким образом, тангенс угла α равен 3/4.
Пример 2: Вычисление угла

Пусть даны синус угла α = 0,6 и косинус угла α = 0,8. Необходимо найти тангенс угла α.
| Дано: | sin(α) = 0,6 |
|---|---|
| cos(α) = 0,8 | |
| Решение: | tan(α) = sin(α) / cos(α) = 0,6 / 0,8 = 0,75 |
| Ответ: | tan(α) = 0,75 |
Использование синуса и косинуса

В математике синус и косинус угла широко используются для вычисления других тригонометрических функций, таких как тангенс. Если известны значения синуса и косинуса угла, то можно легко вычислить тангенс с помощью соответствующих формул.
| Условие: | sin(α) = a, cos(α) = b |
| Формула для тангенса: | tan(α) = a / b |
Например, если известно, что sin(30°) = 0.5 и cos(30°) = √3 / 2, то можно применить формулу для тангенса и вычислить tan(30°) = 0.5 / (√3 / 2) = 1 / √3 = √3 / 3.
Тригонометрические связи

В тригонометрии синус, косинус и тангенс угла связаны между собой следующими соотношениями:
- Синус угла равен отношению противолежащего катета к гипотенузе треугольника.
- Косинус угла равен отношению прилежащего катета к гипотенузе треугольника.
- Тангенс угла равен отношению противолежащего катета к прилежащему катету.
Эти связи позволяют выразить одну тригонометрическую функцию через другие, что упрощает решение различных задач и формул в тригонометрии.
Полезные советы и рекомендации

1. Помните, что для того чтобы найти тангенс угла, необходимо делить синус угла на косинус угла по формуле tg(α) = sin(α) / cos(α).
2. При вычислении тангенса угла убедитесь, что косинус угла не равен нулю, иначе тангенс будет неопределенным.
3. Помните, что значение тангенса угла зависит только от значения синуса и косинуса угла, и не зависит от самого угла.
| Синус угла (sin(α)) | Косинус угла (cos(α)) | Тангенс угла (tg(α)) |
| 0.5 | 0.866 | 0.577 |
| 0.707 | 0.707 | 1.0 |
Вопрос-ответ

Как найти тангенс угла, если известны значения синуса и косинуса?
Если известны синус и косинус угла, то тангенс этого угла можно найти по формуле: тангенс(угла) = синус(угла) / косинус(угла). Например, если sin(α) = 3/5 и cos(α) = 4/5, то tan(α) = 3/5 / 4/5 = 3/4.
Как обычно обозначается тангенс угла?
Тангенс угла обозначается как tg(угла) или tan(угла). Одинаково правильные обозначения для тангенса угла.
В каких случаях требуется находить тангенс угла по значениям синуса и косинуса?
Нахождение тангенса угла по значениям синуса и косинуса пригодится в геометрии, физике, технике и других науках, где требуется работа с углами и треугольниками.
Как можно использовать найденное значение тангенса в дальнейших вычислениях?
Найденное значение тангенса угла может использоваться для вычисления других тригонометрических функций, например, котангенса, секанса, косеканса. Также тангенс угла важен для нахождения углов в прямоугольных треугольниках.
Можете привести пример, как найти тангенс угла по синусу и косинусу?
Допустим, sin(β) = 2/3, cos(β) = 3/4. Тогда tan(β) = sin(β) / cos(β) = (2/3) / (3/4) = 8/9. Таким образом, тангенс угла β равен 8/9.



