Равнобедренный треугольник - это фигура, у которой две стороны и два угла равны. Это значит, что углы у основания равнобедренного треугольника также равны между собой.
Для расчета углов у основания равнобедренного треугольника можно воспользоваться формулой, основанной на свойствах треугольника. Углы при основании (углы между боковой стороной и основанием) равнобедренного треугольника всегда равны.
Используя данную формулу, можно легко определить углы у основания равнобедренного треугольника без необходимости знания всех сторон и углов данной фигуры.
Формула для вычисления угла
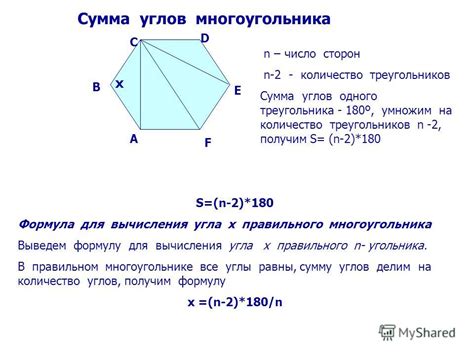
Угол у основания равнобедренного треугольника можно найти по формуле:
- Угол у основания равен половине разницы между 180 градусами и углом при вершине треугольника.
- Формула: \( \text{Угол у основания} = \frac{180^\circ - \text{Угол при вершине}}{2} \).
Основание равнобедренного треугольника
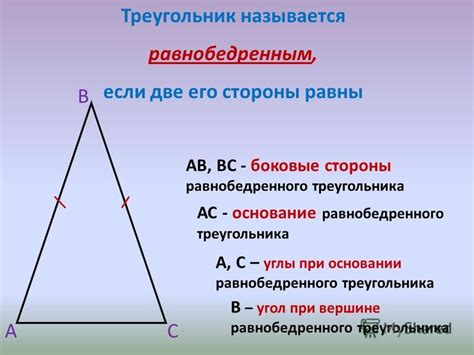
Метод расчета углов у основания равнобедренного треугольника
Рассмотрим равнобедренный треугольник с углом при вершине α и основанием a. По условию равнобедренности углы при основании также равны и обозначаются как β и γ. Для нахождения этих углов используется следующая формула:
| α = (180° - β) / 2 |
| β = α |
| γ = α |
Вопрос-ответ

Какая формула расчета углов у основания равнобедренного треугольника?
Формула расчета углов у основания равнобедренного треугольника: угол при основании равен сумме углов при основании;
Какие основные свойства имеет равнобедренный треугольник?
Основные свойства равнобедренного треугольника: равенство двух сторон треугольника, равенство двух углов при основании, равенство высот и медиан, равенство баз и высот, равенство площадей треугольников;
Каковы условия равенства углов в равнобедренном треугольнике?
Условие равенства углов в равнобедренном треугольнике: углы при основании равны между собой;
Как находят углы у основания равнобедренного треугольника, если известны другие параметры?
Для нахождения углов у основания равнобедренного треугольника, можно использовать теорему косинусов или формулы высчитывания углов прямоугольного треугольника, если известны соответствующие стороны треугольника.



