Основные характеристики рассеивания случайной величины включают в себя дисперсию, среднее квадратическое отклонение, квартили, интерквартильный размах и т.д. Для каждой случайной величины эти характеристики могут быть вычислены и использованы для анализа ее поведения.
Основные свойства функции распределения

Ограниченность: Значения функции распределения всегда лежат в интервале [0, 1]. Минимальное значение равно 0 (вероятность невозможного события), максимальное – 1 (вероятность достоверного события).
Монотонность: Функция распределения возрастает при увеличении значения аргумента. Это означает, что вероятность того, что случайная величина примет значение, не превышающее определенного значения, увеличивается при увеличении этого значения.
Правильная непрерывность справа: Это свойство говорит о том, что вероятность попасть в интервал от a до b включительно равна разности значений функции распределения в точках b и a.
Непрерывность распределения

Декартова система координат
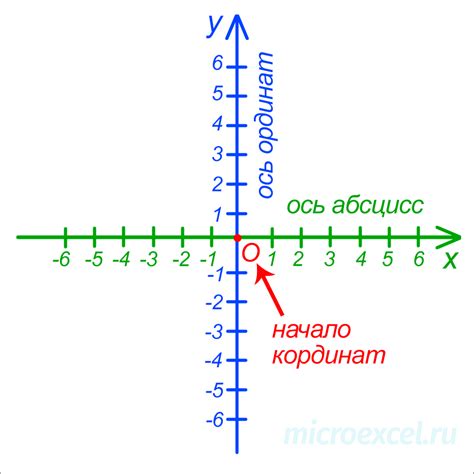
Декартова система координат широко применяется не только в математике, но и в физике, инженерии, экономике и других областях науки.
| Ось | Направление | Положительное направление |
|---|---|---|
| x | Горизонтальная ось | Вправо |
| y | Вертикальная ось | Вверх |
Моменты случайной величины

Центральный момент – это математическое ожидание степени разности случайной величины и её математического ожидания в степени k.
Начальный момент – это математическое ожидание степени случайной величины в степени k.
Центральный момент степени k – это математическое ожидание степени разности случайной величины и её математического ожидания в степени k.
Энтропия и информация

Информация, с точки зрения теории информации, обратно пропорциональна вероятности сообщения. Информативность высока, когда вероятность происшествия события низкая, и наоборот. Таким образом, информация более ценна, когда она неожиданна и необычна.
Специальные типы распределения
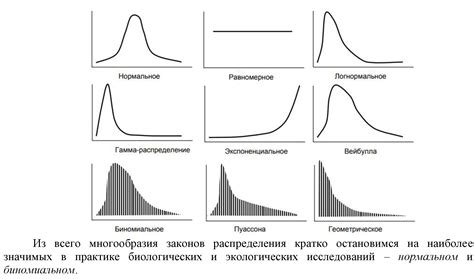
Существуют различные специальные типы распределений, которые используются для моделирования различных случайных величин:
Биномиальное распределение: применяется для описания случайных экспериментов с фиксированным числом испытаний, в каждом из которых результат может быть только двух видов (успех или неудача).
Пуассоновское распределение: характеризует число событий, происходящих за фиксированное время или в фиксированном пространстве, при условии, что события происходят независимо друг от друга.
Геометрическое распределение: моделирует число испытаний, необходимых для первого успеха в серии независимых испытаний, каждое из которых может закончиться успехом или неудачей.
Экспоненциальное распределение: описывает время между последовательными событиями в потоке событий, где вероятность события не зависит от прошлого.
Вопрос-ответ

Что такое рассеивание случайной величины?
Рассеивание случайной величины - это мера разброса значений случайной величины относительно её математического ожидания. Оно показывает, насколько далеко от среднего значения могут находиться конкретные значения случайной величины. Чем больше значение дисперсии (квадратный корень из дисперсии называется стандартным отклонением), тем больший разброс имеют значения случайной величины.
Как можно рассчитать рассеивание случайной величины?
Для рассчета рассеяния случайной величины нужно вычислить дисперсию этой случайной величины. Дисперсия случайной величины равна среднему квадрату отклонения каждого значения случайной величины от её математического ожидания. Для этого необходимо посчитать математическое ожидание случайной величины, вычесть из каждого значения величины математическое ожидание, возвести разности в квадрат, сложить результаты и поделить на количество значений.
Чем отличается дисперсия от стандартного отклонения случайной величины?
Дисперсия случайной величины - это средний квадрат отклонений значений случайной величины от её математического ожидания. Стандартное отклонение случайной величины является квадратным корнем из дисперсии. Дисперсия измеряется в квадратных единицах и показывает разброс значений случайной величины, в то время как стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, и позволяет интерпретировать разброс значений в более понятных единицах.
Почему важно знать рассеивание случайной величины?
Знание рассеивания случайной величины важно для оценки степени вариации значений этой величины. Это позволяет понять, насколько предсказуемы или случайны могут быть результаты, связанные с данной случайной величиной. Чем больше рассеивание, тем больше вероятность большого разброса значений и наоборот. Знание рассеивания помогает принимать взвешенные решения, основанные на вероятностях и степени неопределённости.



