Логарифмическая функция – одна из основных математических функций, которая играет важную роль в различных областях науки и техники. Она обладает множеством интересных свойств и особенностей, и одной из них является возможность наличия экстремумов в её области определения.
В данной статье мы рассмотрим процесс исследования наличия экстремумов у логарифмической функции. Мы изучим условия, при которых эта функция может иметь точки минимума или максимума и определим способы их нахождения с использованием методов математического анализа.
Проведение такого исследования позволяет лучше понять поведение логарифмической функции, а также применить полученные знания в решении различных практических задач, связанных с оптимизацией, моделированием и анализом данных.
Исследование экстремумов логарифмической функции
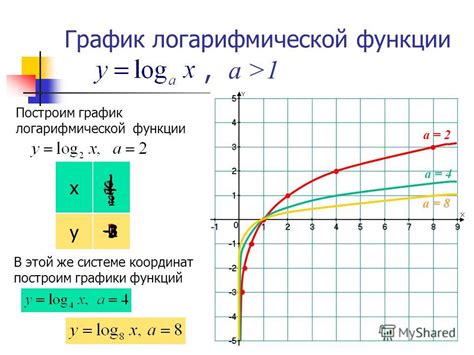
Логарифмическая функция имеет уникальные свойства и может иметь экстремумы. Для исследования экстремумов логарифмической функции необходимо выяснить, где она может достигать максимальных или минимальных значений.
Для этого следует проанализировать производные функции и найти их нули. В случае логарифмической функции y = ln(x), ее производная равна 1/x. Таким образом, экстремумы могут находиться в точках, где производная равна нулю или не существует.
После нахождения возможных точек экстремумов следует провести исследование при помощи второй производной, чтобы определить тип экстремума - максимум или минимум.
Определение и свойства функции при исследовании
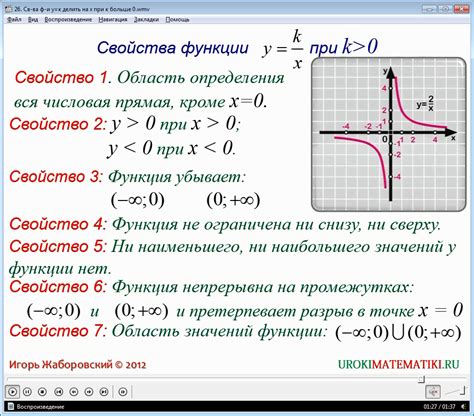
| 1. Область определения: | \((0, +\infty)\) |
| 2. Область значений: | \((-\infty, +\infty)\) |
| 3. График: | Убывающая функция с асимптотой \(y = 0\) и горизонтальной асимптотой \(x = 0\) |
| 4. Экстремумы: | Логарифмическая функция не имеет экстремумов |
Нахождение точек экстремума с помощью производной
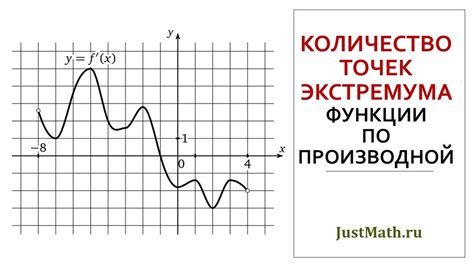
Для того чтобы найти экстремумы функции, заданной логарифмическим выражением, необходимо использовать производную. Экстремумы функции соответствуют точкам, где производная равна нулю или не существует.
Для логарифмической функции f(x) = ln(x), производная будет f'(x) = 1/x. Чтобы найти точки экстремума, необходимо решить уравнение f'(x) = 0.
Анализируя решения данного уравнения, можно найти точки, в которых функция имеет локальные максимумы, минимумы или точки перегиба. Для того чтобы классифицировать экстремумы, можно провести второй производный тест.
Анализ графика функции для подтверждения результатов

Способы проверки точек экстремума на минимум и максимум
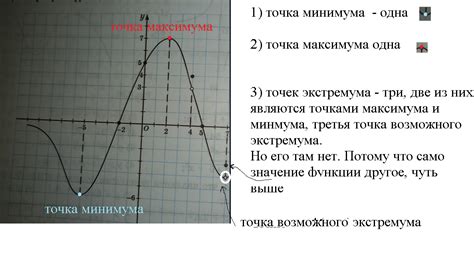
Существует несколько способов проверки точек экстремума на минимум и максимум:
- Первый способ заключается в вычислении второй производной и анализе её знака в точке. Если вторая производная положительна, то точка является точкой минимума, а если она отрицательна – точкой максимума.
- Второй способ – использование первой производной. Если первая производная меняет знак с «+» на «-» при переходе через точку, то это может свидетельствовать о наличии экстремума. Точная природа экстремума определяется дальнейшим анализом.
- Третий способ – поиск точек, в которых первая производная равна нулю. Эти точки могут быть кандидатами на точки экстремума, и следует дополнительно анализировать их при помощи второй производной или изменения знака первой производной.
Вопрос-ответ

Что такое логарифмическая функция?
Логарифмическая функция — это функция вида f(x) = loga(x), где a - основание логарифма, а x - аргумент функции. Такая функция определена только для положительных аргументов x. Логарифмическая функция показывает степень, в которую необходимо возвести основание a, чтобы получить значение x.
Как исследовать наличие экстремумов у логарифмической функции?
Для исследования наличия экстремумов у логарифмической функции f(x) = loga(x) следует найти производную этой функции. Затем исследовать производную на монотонность и найти точки, где производная равна нулю или не существует. После этого анализировать поведение функции в окрестностях найденных точек для определения экстремумов.
Как выглядит график логарифмической функции?
График логарифмической функции f(x) = loga(x) характеризуется тем, что он стремится к горизонтальной асимптоте y = 0 при x → +∞ и уходит в бесконечность при x → 0. Для разных значений основания a форма графика логарифмической функции может различаться.
Какие свойства имеет логарифмическая функция?
Логарифмическая функция обладает некоторыми важными свойствами, такими как: 1) loga(1) = 0 для любого основания a; 2) loga(a) = 1; 3) loga(b) + loga(c) = loga(bc); 4) loga(b) - loga(c) = loga(b/c) и другие свойства, упрощающие работу с логарифмами.



