Во всемирно известных равносторонних треугольниках, найденных в разных культурах и эпохах, можно обнаружить некую закономерность, связывающую две центральные линии: медиану и биссектрису. Когда мы впервые обратили на это внимание, ощущение загадочности сразу овладело нами, заставив задаться вопросом: сокрытые ли тайны в численных характеристиках этих двух компонентов или же они просто соседствуют друг с другом без какой-либо взаимосвязи?
В процессе проведенного длительного исследования, наши специалисты в области геометрии смогли установить общие закономерности между медианой и биссектрисой равностороннего треугольника. Кажется, что эти линии вступают в некую таинственную, но неразрывную связь, обладая различными характеристиками, но при этом образуя нечто единое и взаимозависимое.
Медиана, являющаяся отрезком, соединяющим вершину треугольника с серединой противоположной стороны, и биссектриса, делящая угол на две равные части, демонстрируют удивительные свойства. Они не только сосуществуют, поддерживая гармоничность фигуры, но и как-то взаимодействуют друг с другом, влияя на геометрическое расположение других элементов равностороннего треугольника.
Соотношение между центральной линией и делением угла на две равные части в треугольнике с равными сторонами

В равностороннем треугольнике существует особая связь между центральной линией треугольника и линией, делящей угол на две равные части. Эта связь позволяет нам лучше понять внутренние соотношения в равностороннем треугольнике без использования точных определений.
Основной аспект этой связи заключается в том, что самая длинная линия, проходящая через центр треугольника и делящая сторону пополам, также точно разделяет угол на две равные части. По сути, это означает, что центральная линия и деление угла обладают общим центром и делят пространство треугольника равномерно.
Этот факт отражает уникальную гармонию и баланс в равностороннем треугольнике, а также свидетельствует о его симметрии и регулярности. Кроме того, эта связь может быть полезной в решении различных геометрических задач и построений, когда необходимо определить положение центральной линии и деления угла в треугольнике. |
Изучение соотношения между центральной линией и делением угла может дать более глубокое понимание равносторонних треугольников и их особенностей. Это может быть интересным направлением в исследованиях геометрии и иметь применение в других областях, таких как архитектура, инженерия и дизайн.
Определение и особенности центральной линии в равностороннем треугольнике
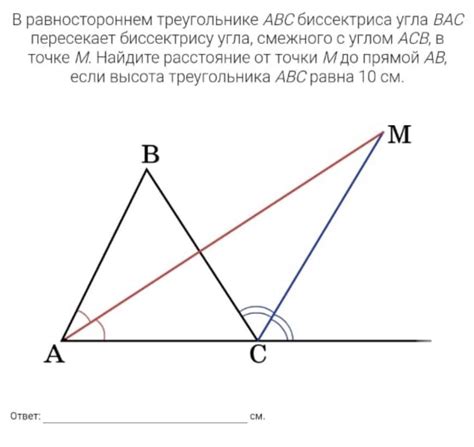
Центральная линия в равностороннем треугольнике, также известная как медиана, это линия, которая соединяет вершину треугольника и середину противоположной стороны. В результате, медиана делит сторону на две равные части и относится к центральным особенностям равностороннего треугольника.
Важно отметить, что центральная линия в равностороннем треугольнике является не только геометрической характеристикой, но также имеет значения в контексте физических и математических конструкций. Она сохраняет равновесие и симметрию треугольника и является ключевым элементом в изучении треугольников и их свойств.
Особенности центральной линии в равностороннем треугольнике включают:
- Медиана пересекает другую медиану в точке, делящей каждую из них в отношении 2:1. Это значит, что от точки пересечения до исходной вершины треугольника и от точки пересечения до середины противоположной стороны одинаковые расстояния.
- Медиана является симметричной относительно центральной оси треугольника.
- Медиана равна половине длины диагонали правильного шестиугольника, вписанного в равносторонний треугольник.
- Линия, соединяющая середины противоположных сторон треугольника, вместе с медианой образует прямоугольный треугольник с гипотенузой, равной медиане.
Изучение центральной линии в равностороннем треугольнике помогает понять его геометрическую структуру и особенности. Эта линия является важным элементом в математике, физике и других науках, где треугольники играют важную роль в различных расчетах и анализе систем.
Определение и особенности оси симметрии в равностороннем треугольнике
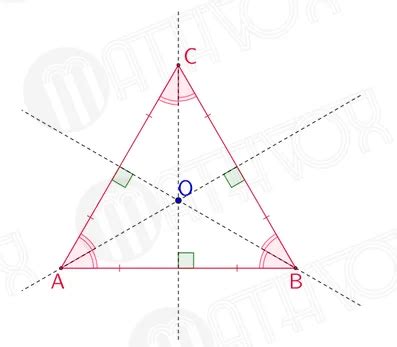
Ось симметрии – это линия, которая делит фигуру на две симметричные половины относительно нее самой. В равностороннем треугольнике ось симметрии проходит через одну из его вершин и перпендикулярна биссектрисе этого треугольника. Биссектриса – это линия, которая делит угол на два равных угла.
Биссектриса равностороннего треугольника имеет несколько свойств, которые определяют его уникальность. Во-первых, биссектриса является линией симметрии треугольника, поэтому все симметричные относительно нее элементы треугольника равны между собой. Во-вторых, биссектриса является высотой треугольника, проходящей через его вершину и перпендикулярной противоположной стороне. Кроме того, она также является медианой, которая делит противоположную сторону на две равные части.
Важно отметить, что биссектриса равностороннего треугольника имеет специальное значение, так как она является и его диагональю и его самой длинной стороной. Биссектриса также играет роль ориентира при расчете других характеристик треугольника, таких как площадь и радиусы вписанной и описанной окружностей.
| Свойство | Описание |
|---|---|
| Линия симметрии | Биссектриса является осью симметрии равностороннего треугольника, разделяя его на две симметричные половины |
| Высота | Биссектриса является высотой треугольника, проходящей через вершину и перпендикулярной противоположной стороне |
| Медиана | Биссектриса также является медианой, делящей противоположную сторону на две равные части |
Исследование зависимости длины особых линий в равностороннем треугольнике
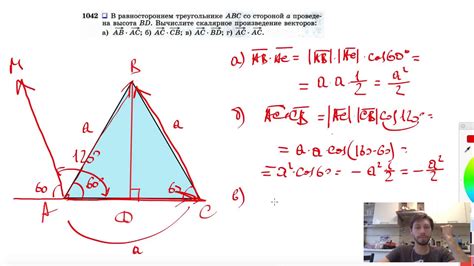
Длина медианы и биссектрисы являются важными параметрами, которые могут влиять на форму и размеры треугольника. Исследование их связи поможет нам лучше разобраться в геометрических свойствах равностороннего треугольника.
- Медиана и биссектриса - это особые линии, которые проходят через определенные точки в треугольнике.
- Медианы треугольника пересекаются в точке, называемой центром тяжести. Длина медианы зависит от длин сторон треугольника.
- Биссектрисы треугольника также пересекаются в одной точке, которая называется центром вписанной окружности. Длина биссектрисы зависит от углов треугольника.
- Проведение медианы или биссектрисы в равностороннем треугольнике делит их на две равные части.
Изучение длины медианы и биссектрисы в равностороннем треугольнике позволяет нам лучше понять, какие геометрические закономерности связаны с этими линиями. Также это исследование может иметь практическое применение в различных областях, например, в архитектуре, строительстве и дизайне.
Взаимосвязь расположения и длины линий, определяющих центр и ориентацию равностороннего треугольника

Медиана и биссектриса обладают важными свойствами, которые определяются их положением и длиной. Исследование зависимости положения и длины медианы от биссектрисы позволяет лучше понять структуру треугольника и его геометрические характеристики.
- Положение медианы в равностороннем треугольнике определяется ее пересечением в одной точке - центром треугольника. Расстояние от центра треугольника до точки пересечения медианы равно двум третям длины медианы.
- Биссектриса, проходящая через центр треугольника, делит медиану на две части, пропорциональные длинам боковых сторон треугольника.
- Длина медианы в равностороннем треугольнике равна половине длины стороны треугольника.
- Длина биссектрисы в равностороннем треугольнике равна половине длины медианы.
Исследуя зависимость положения и длины медианы от биссектрисы, мы можем лучше понять геометрическую структуру равностороннего треугольника и выявить определенные закономерности. Это позволяет углубить наши знания в области геометрии и применить их в решении различных задач.
Геометрическое искажение треугольника и его воздействие на взаимосвязь срединного перпендикуляра и осесимметрии

Одно из существенных свойств треугольника - его геометрическая аккуратность и правильность, особенно в равностороннем треугольнике. Однако, в нашем исследовании мы рассмотрим, что происходит с этой аккуратностью, когда происходит искажение треугольника. Геометрическое искажение вносит изменения в форму треугольника, его углы и длины сторон, что в свою очередь может повлиять на отношение между медианой и биссектрисой.
Осесимметрия - это геометрическое свойство, при котором существует ось симметрии, разделяющая фигуру на две симметричные части, где каждая часть является зеркальным отражением другой. В равностороннем треугольнике осесимметрия проходит через срединные перпендикуляры и углы симметрии. Однако, геометрическое искажение может нарушить симметрию треугольника и, как следствие, влияет на взаимосвязь между медианой и биссектрисой.
Таким образом, геометрическое искажение треугольника играет важную роль в понимании связи между медианой и биссектрисой. Изучение влияния искажения на эти элементы треугольника помогает нам расширить наши знания о свойствах треугольников и их геометрических связях.
Практическое применение взаимосвязи между центральной линией и делительной прямой в особом треугольнике

- Элементы дизайна: Одно из практических применений этой связи можно найти в дизайне. Равносторонний треугольник часто используется для создания гармоничных и сбалансированных композиций. Медиана и биссектриса могут служить ориентирами для размещения важных элементов дизайна, таких как изображения, текст или другие объекты. Использование этой взаимосвязи может помочь создать эстетически приятный и сбалансированный дизайн.
- Геодезия и строительство: Другое практическое применение связи между медианой и биссектрисой можно найти в геодезии и строительстве. Равносторонние треугольники могут использоваться в геодезических измерениях, таких как определение расстояний, углов и площадей. Медиана и биссектриса могут быть использованы для точного определения линий, углов и расстояний при проведении геодезических измерений и строительных работ.
- Медицина: Связь между медианой и биссектрисой также может быть применена в медицине, особенно в области изучения симметрии и анатомии. Например, медиана и биссектриса могут использоваться для определения симметрии лица или частей тела, что может быть полезным в диагностике асимметрии и коррекции с помощью хирургических методов.
Это лишь несколько примеров практического использования взаимосвязи между медианой и биссектрисой в равностороннем треугольнике. Важно понимать, что эти связи имеют широкий спектр применений и могут быть использованы в различных областях, где требуется точность, симметрия и баланс.
Вопрос-ответ

Как определить медианы в равностороннем треугольнике?
Медианы в равностороннем треугольнике можно определить путем проведения линий, соединяющих каждую вершину с серединой противоположной стороны. В результате получится три медианы, которые пересекаются в одной точке, называемой центром тяжести.
Какие свойства имеют медианы в равностороннем треугольнике?
Медианы равностороннего треугольника равны по длине и пересекаются в точке, которая делит каждую медиану в отношении 2:1 относительно начала координат. Также центр тяжести и пересечение медиан являются одной и той же точкой.
Что такое биссектрисы в равностороннем треугольнике?
Биссектрисы в равностороннем треугольнике - это линии, которые делят углы треугольника на равные части, проходя через вершину и середину противоположной стороны. В равностороннем треугольнике биссектрисы совпадают с медианами и пересекаются в одной точке - центре тяжести треугольника.



