Исследователи всегда задаются вопросом: что есть медиана в равностороннем треугольнике? Определение этого явления часто вызывает споры и разногласия между математиками и физиками. Все дело в том, что понятие медианы в данном контексте имеет несколько эквивалентных терминов, но каждый из них содержит свою специфику и отражает определенные свойства треугольника.
Когда мы говорим о медиане, чаще всего представляется идея высоты, тянущейся из одной вершины к середине противоположной стороны. Но это не все! Существуют и другие ракурсы, из которых рассматривается медиана. Например, ее можно описать как отрезок, соединяющий вершину с серединой основания, противоположенного данной вершине. При этом, угол между медианой и основанием составляет ровно 60 градусов, что является одним из фундаментальных свойств равностороннего треугольника.
Итак, медиана в равностороннем треугольнике - это не просто вертикальное расстояние, измеряемое от одной точки до другой, но и концепция, охватывающая разные аспекты исследования. В данной статье мы рассмотрим все аспекты медианы, ее отношение к высоте и другим геометрическим параметрам треугольника. И, конечно, попытаемся разобраться в том, является ли идея медианы в равностороннем треугольнике истинной высотой или всего лишь ошибочным представлением.
Обманчивое впечатление медианы в треугольнике с равными сторонами
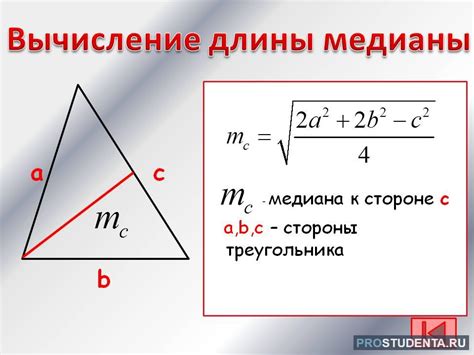
В равностороннем треугольнике иногда возникает обманчивое впечатление относительно функции медианы. Однако, чтобы глубже понять это явление, необходимо разобраться в сущности и нюансах геометрии представленной фигуры.
Складываясь из трех равных сторон, равносторонний треугольник всегда вызывает интерес и демонстрирует свою привлекательность. Казалось бы, симметричность и совершенство его формы создают представление, будто все трех его медиан должны быть равными, а также существовать корреляция между медианой и высотой. Однако это впечатление обманчиво.
- «Медиана в равностороннем треугольнике»: принятый термин, который на самом деле представляет собой отрезок, соединяющий одну из вершин с серединой противоположной стороны.
- Роль медианы в рассматриваемом типе треугольника: зачастую медиана воспринимается как линия, перпендикулярная соответствующей стороне и проходящая через середину противоположной стороны. При этом создается впечатление, будто медиана является высотой.
- Структурные особенности равностороннего треугольника: его трое медиан равны, однако не совпадают с высотами, создавая иллюзию одинаковости.
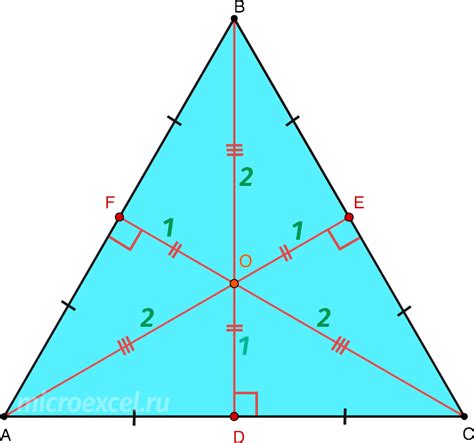
- Реальное расположение медиан: медианы пересекаются в одной точке, называемой центром тяжести треугольника. Они делятся в ней в отношении 2:1.
Таким образом, несмотря на обманчивое впечатление, создаваемое равносторонним треугольником, его медианы не являются высотами. Использование специфического термина "медиана" в данном контексте может привести к неправильному пониманию роли и функции линий в этой геометрической фигуре.
Свойства медианы в треугольнике с равными сторонами
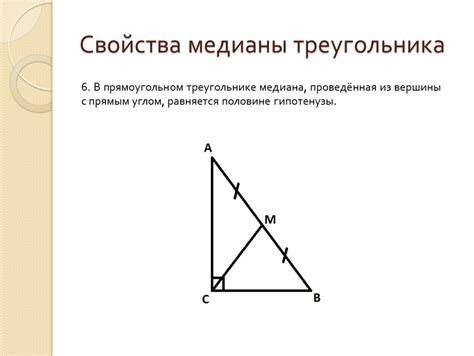
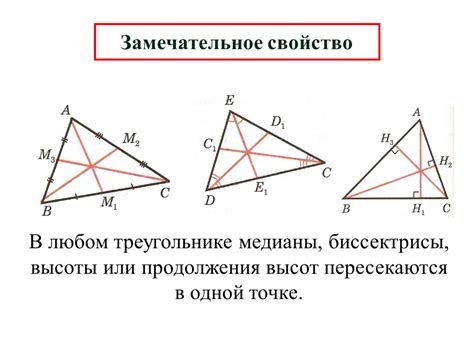
Одним из ключевых свойств медианы в равностороннем треугольнике является то, что она проходит через точку пересечения трех медиан. Это означает, что все медианы в равностороннем треугольнике пересекаются в одной точке, которая называется центром тяжести или барицентром треугольника. Данное свойство позволяет точно определить положение медианы в треугольнике и устанавливает ее важную роль в геометрии.
Кроме того, медиана в равностороннем треугольнике является радиусом вписанной окружности. Это означает, что отрезок, соединяющий середину стороны треугольника с вершиной, является радиусом окружности, которая полностью лежит внутри треугольника и касается всех его сторон. Такое свойство медианы позволяет использовать ее для решения задач, связанных с вписанными окружностями в равносторонних треугольниках.
| Свойства медианы в равностороннем треугольнике | Объяснение |
|---|---|
| Проходит через центр тяжести | Все медианы в равностороннем треугольнике пересекаются в одной точке - центре тяжести или барицентре треугольника. |
| Является радиусом вписанной окружности | Медиана в равностороннем треугольнике представляет собой радиус окружности, которая полностью лежит внутри треугольника и касается всех его сторон. |
Медиана как линия баланса внутри треугольника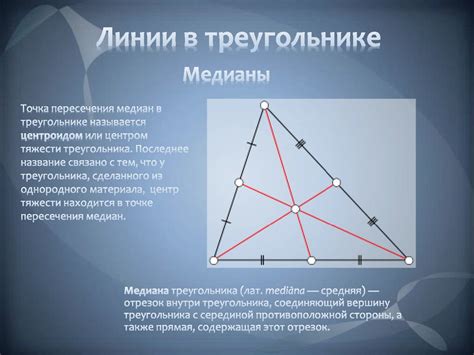 |
Представьте треугольник в виде весовых чаш, размещенных на концах медианы. Каждая сторона треугольника представляет определенный вес, который влияет на его равновесие. Если стороны треугольника представляют собой одинаковые значения, то медиана будет находиться точно в центре треугольника. Это создает идеальное равновесие, где все стороны и углы равны друг другу. Однако, если стороны треугольника имеют разные значения, точка баланса смещается от центра, указывая на неравномерность внутри треугольника.
Медиана является визуальным и математическим показателем гармонии в треугольнике. Она помогает определить, насколько каждая сторона влияет на общую структуру треугольника, а также какие изменения могут привести к его более сбалансированному состоянию. Рассмотрение медианы как линии баланса позволяет лучше понять внутреннюю гармонию исследуемого треугольника и его взаимосвязь с другими геометрическими формами.
Понятие истинной высоты треугольника: размышления о его сути

Когда мы говорим о высоте треугольника, часто приходит на ум образ равномерного подъема и опускания. Однако, обычное представление о высоте может быть ошибочным и не полностью отражать глубину и сущность этого геометрического понятия. Истинная высота треугольника отображает его внутреннюю гармонию и уникальную конфигурацию.
Треугольник, как многогранный объект, обладает своими особенностями и закономерностями. Высота, как важная характеристика треугольника, играет важную роль в его структуре и связях с другими элементами. Она позволяет нам увидеть его внутренние пропорции и соотношения.
В высоте треугольника нет места для поверхностного представления о простом подъеме и опускании. Она выражает глубину, связь сторон и точек в его внутреннем пространстве. Истинная высота треугольника является неотъемлемой частью его геометрической сущности и помогает нам увидеть его истинное лицо.
Зависимость истинной высоты от равных сторон треугольника
В данном разделе будем исследовать зависимость между истинной высотой и длиной равных сторон треугольника. Обратим внимание на то, как изменение длины сторон влияет на высоту треугольника и как данная зависимость может быть полезна при изучении геометрии.
Рассмотрим случай равностороннего треугольника, основное свойство которого заключается в том, что все три стороны имеют одинаковую длину. Очевидно, что высота является одной из важных характеристик треугольника, так как определяет расстояние от вершины до основания. Однако, часто существует некоторая путаница в понятии "истинной высоты", что может приводить к ошибочным представлениям.
Проанализируем связь между равными сторонами треугольника и его высотой, исследуя различные величины на примере конкретных значений. Обратим внимание на то, что при увеличении или уменьшении длины сторон, истинная высота также будет изменяться, что является весьма интересным аспектом в изучении свойств равносторонних треугольников.
Иллюзия: понятие высоты в равностороннем треугольнике
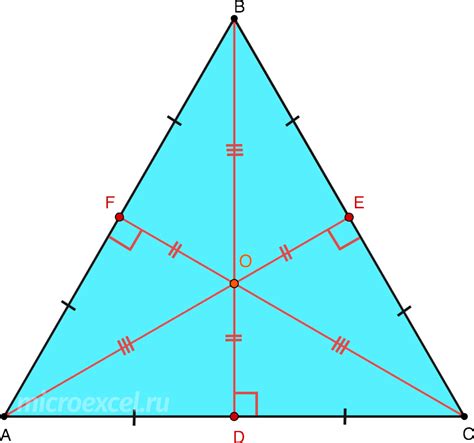
Возможно, традиционное представление о высоте в равностороннем треугольнике скрывает за собой несколько аспектов, которые могут привести к неправильному восприятию этой геометрической фигуры. Под воздействием определенных факторов, таких как медиана, могут возникнуть иллюзии, distortions или искажения, которые вводят в заблуждение наше восприятие.
Различие между вертикальной прямоугольной линией и точкой пересечения медиан в специальном треугольнике

В специальном треугольнике с углом, равным 60 градусам, существует различие между двумя важными элементами: вертикальной прямоугольной линией и точкой пересечения медиан. Хотя оба этих элемента связаны с геометрическими характеристиками треугольника, их использование и значения отличаются друг от друга.
Вертикальная прямоугольная линия проходит через вершину треугольника и создает перпендикулярное соединение с противоположной стороной. Она является высотой треугольника и используется для измерения расстояния от базы до вершины. Вертикальная прямоугольная линия создает прямой угол со своей проекцией на базовую сторону, что делает ее полезной для вычисления геометрических свойств треугольника.
С другой стороны, точка пересечения медиан является центром тяжести треугольника. Она обозначает точку, где тяжелоцентральные линии каждой из трех медиан пересекаются. Медианы являются линиями, которые соединяют каждую вершину треугольника с серединой противоположной стороны. Точка пересечения медиан является центром тяжести, в котором равномерно распеределен вес треугольника.
- Вертикальная прямоугольная линия представляет собой высоту треугольника, важную для рассчетов площади и теоремы Пифагора.
- Точка пересечения медиан является геометрическим центром треугольника, испольуемым в задачах гравитации и механике.
Таким образом, вертикальная прямоугольная линия и точка пересечения медиан - это два разных элемента в специальном треугольнике. Вертикальная линия представляет собой высоту, определенную высотой треугольника, в то время как точка пересечения медиан является центром тяжести, где равномерно распределен вес треугольника. Каждый элемент вносит свой вклад в понимание и анализ геометрических и механических свойств треугольника.
Когда центральная линия и вертикальная прямая совпадают?

Как же может возникнуть ситуация, когда медиана и вертикальная прямая совпадают? Это имеет место быть в специальных случаях, когда равносторонний треугольник оказывается таким, что одна из его медиан совпадает с его вертикальной прямой, которая является истинной высотой треугольника. В таких треугольниках медианы оказываются выпуклыми внутрь треугольника и пересекаются в одной точке, которая является и центром треугольника.
Практическое использование медианы и истинной высоты в реальной жизни
В данном разделе мы рассмотрим практические примеры применения концепций медианы и истинной высоты треугольника в реальной жизни. Несмотря на то, что эти термины могут показаться сложными и абстрактными, на самом деле они имеют применение в различных областях, от архитектуры до физики.
Одним из примеров использования медианы треугольника является конструкция мостов. При проектировании мостов необходимо обеспечить их стабильность и прочность, чтобы они могли выдерживать вес транспортных средств и сильные нагрузки. Медиана является одним из важных аспектов в расчетах и дизайне мостов, поскольку она помогает определить точку баланса и равномерное распределение нагрузки на конструкцию.
Истинная высота треугольника также находит свое применение в реальной жизни. Например, в геодезии и картографии она используется для определения высот горных вершин или других неровностей на земной поверхности. С помощью истинной высоты можно точно измерить высоту объектов и географических формаций, что в свою очередь помогает строить детальные карты и проводить геологические и географические исследования.
Но медиана и истинная высота не ограничиваются только техническими областями. Они также имеют применение в искусстве и дизайне. Например, в художественной композиции медиана может использоваться для создания гармоничного расположения объектов, подчеркивая симметрию и баланс в произведении. Истинная высота, в свою очередь, может быть использована для создания плоскостных эффектов или эффектов глубины в живописи, скульптуре и других видов искусства.
| Применение медианы | Применение истинной высоты |
|---|---|
| Проектирование мостов | Определение высот горных вершин |
| Расчет равномерного распределения нагрузки | Создание детальных карт |
| Художественная композиция | Искусство и дизайн |
Проблемы измерений и вычислений при определении медианы и истинной высоты
Вопрос-ответ

Как определить медиану в равностороннем треугольнике?
Медиана в равностороннем треугольнике проводится из вершины к середине противоположной стороны.
Что такое истинная высота треугольника?
Истинная высота треугольника - это отрезок, проведенный из вершины треугольника перпендикулярно его основанию.
Каковы основные свойства медианы в равностороннем треугольнике?
Основные свойства медианы в равностороннем треугольнике: все медианы равны между собой, пересекаются в одной точке - центре окружности, вписанной в треугольник.
Существует ли связь между медианой и истинной высотой в равностороннем треугольнике?
Да, в равностороннем треугольнике медиана совпадает с истинной высотой, так как они проведены по одной и той же линии.
Чему равен угол между медианой и основанием равностороннего треугольника?
Угол между медианой и основанием равностороннего треугольника равен 60 градусам. Все углы равностороннего треугольника равны 60 градусам.
Может ли медиана служить истинной высотой в равностороннем треугольнике?
В равностороннем треугольнике, все медианы, высоты и биссектрисы совпадают, поэтому медиана может служить истинной высотой.



