Диаметр цилиндра – один из ключевых параметров, определяющих его геометрические характеристики. Часто возникает необходимость определить диаметр цилиндра по известной длине его окружности. В данной статье мы рассмотрим различные методы расчета диаметра цилиндра и посмотрим, каким образом можно выполнить эту задачу.
Одним из самых простых способов определения диаметра цилиндра по длине окружности является использование основных свойств геометрических фигур. Связь между диаметром и окружностью цилиндра позволяет нам вывести формулу, которая позволит нам точно определить значение диаметра.
Методы расчета диаметра цилиндра по длине окружности
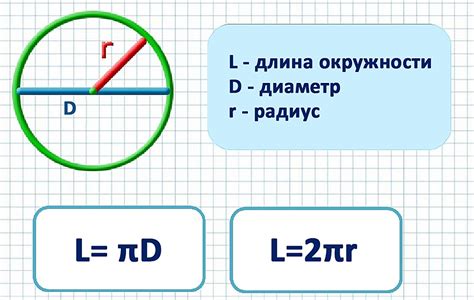
Если известна длина окружности цилиндра, можно выразить диаметр по формуле: d = C / π. Просто подели длину окружности на число π и получишь значение диаметра цилиндра.
Использование формулы диаметра цилиндра
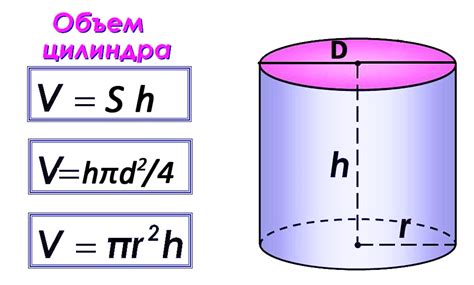
Для определения диаметра цилиндра по длине окружности можно использовать следующую формулу:
Диаметр цилиндра = Длина окружности / π
Где π (pi) - математическая константа, приблизительно равная 3.14159. Подставив значение длины окружности, можно легко вычислить диаметр цилиндра.
Измерение окружности и вычисление диаметра
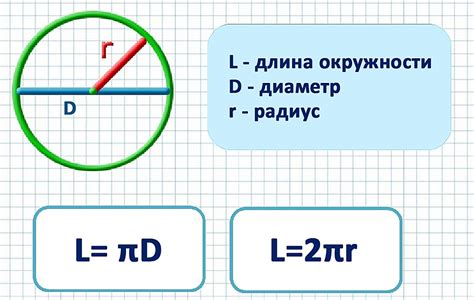
Для определения диаметра цилиндра по длине окружности существует несколько методов. Один из них основан на измерении самой окружности. Для этого необходимо использовать мерную ленту или иную измерительную линейку, обернуть ее вокруг цилиндра, измерить полученное значение длины окружности в сантиметрах или дюймах.
После того как длина окружности измерена, можно вычислить диаметр цилиндра по формуле: D = L / π, где D - диаметр, L - длина окружности, π - число пи, приблизительно равное 3,14. После вычисления полученное значение диаметра следует округлить до нужного количества знаков после запятой в соответствии с требованиями точности измерения.
Применение метода секущей

1. Задать уравнение, описывающее зависимость диаметра от длины окружности.
2. Выбрать две начальные точки и построить через них секущую линию.
3. Вычислить точку пересечения с осью абсцисс – это оценка диаметра цилиндра.
4. Повторять шаги 2-3, приближаясь к истинному значению диаметра.
Анализ отношения длины окружности к диаметру

Отношение длины окружности к диаметру известно как число π (пи). Это постоянное число, приблизительно равное 3,14159. Зная длину окружности, можно легко определить диаметр, разделив длину на π. Таким образом, формула для расчета диаметра по длине окружности выглядит следующим образом: диаметр = длина окружности / π.
Точные методы определения диаметра цилиндра

Существует несколько точных методов определения диаметра цилиндра по длине окружности:
| 1. Использование формулы длины окружности: | Диаметр цилиндра можно определить по формуле: d = L / π, где d - диаметр, L - длина окружности, π - число пи. |
| 2. Прямое измерение: | Используйте средство измерения, например, ленту, чтобы измерить длину окружности, затем используйте формулу для расчета диаметра. |
| 3. Метод с использованием цифровых инструментов: | Используйте цифровой измеритель для измерения длины окружности и получения точного значения диаметра. |
Использование геометрических принципов для расчета

Для определения диаметра цилиндра по длине окружности можно использовать геометрические принципы. Известно, что длина окружности вычисляется по формуле:
Длина окружности = π * диаметр,
где π (пи) – математическая константа, приблизительно равная 3.14159. Таким образом, диаметр цилиндра можно найти, разделив длину окружности на π:
Диаметр = Длина окружности / π.
С помощью этой формулы и известной длины окружности можно легко вычислить диаметр цилиндра, используя геометрические принципы.
Различные способы нахождения диаметра по окружности

Для определения диаметра цилиндра по длине окружности можно воспользоваться следующими методами:
1. Формула диаметра по окружности:
Для вычисления диаметра по длине окружности используется формула: диаметр = длина окружности / π. Здесь π (пи) принимается как 3,14 или более точное значение в зависимости от требуемой точности расчета.
2. Угловая мера в градусах:
Другой способ - использование угловой меры, выраженной в градусах, для нахождения диаметра. Таким образом, можно воспользоваться формулой: диаметр = длина окружности / (угловая мера в градусах * π / 180).
Выбирая подходящий метод расчета, вы сможете определить диаметр цилиндра по длине окружности с требуемой точностью и без дополнительных сложностей.
Сравнение эффективности различных методов расчета цилиндра
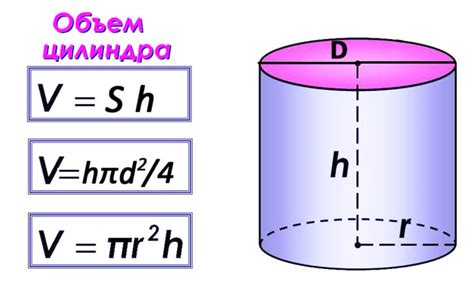
При определении диаметра цилиндра по длине окружности можно использовать различные методы. Рассмотрим некоторые из них:
- Метод, основанный на формуле для нахождения длины окружности:
Для этого метода необходимо знать формулу длины окружности - Л = π * d, где d - диаметр. Следовательно, d = Л / π. Этот метод прост в вычислении, но требует знания математической формулы.
- Метод, использующий формулу для нахождения площади круга:
Круговая площадь вычисляется по формуле S = π * (d/2)^2. Таким образом, для нахождения диаметра можно воспользоваться формулой: d = 2 * √(S / π). Этот метод требует знания формулы площади круга.
- Метод, основанный на измерении обхвата цилиндра и математическом анализе:
Если есть возможность измерить обхват цилиндра, то диаметр можно найти, разделив обхват на π (d = Л / π). Этот метод не требует знания математических формул, но требует точных измерений.
Выбор метода зависит от доступных данных и предпочтений оператора.
Вопрос-ответ

Как определить диаметр цилиндра по известной длине окружности?
Для определения диаметра цилиндра по известной длине окружности необходимо разделить длину окружности на число Пи (π). То есть диаметр равен отношению длины окружности к числу Пи: D = C / π.
Какие методы расчета используются для определения диаметра цилиндра по длине окружности?
Для определения диаметра цилиндра по длине окружности используют один основной метод, который заключается в делении длины окружности на число Пи (π), чтобы получить значение диаметра.
Можно ли определить диаметр цилиндра без знания его длины окружности?
Для определения диаметра цилиндра необходимо знать либо его длину окружности, либо другие измерения (площадь поверхности, объем и т.д.). Без этой информации определить диаметр невозможно.



