Параллельность прямых - одно из основных понятий в геометрии. Два прямых называются параллельными, если они лежат в одной плоскости и не пересекаются. Существует несколько способов доказательства параллельности прямых, каждый из которых основан на определенных свойствах и аксиомах геометрии.
Один из классических способов доказательства параллельности прямых основан на использовании понятия углов. Два прямых считаются параллельными, если у них соответственные углы равны или сумма этих углов равна 180 градусам. Проводя через пересекающиеся прямые третью прямую, можно использовать свойства углов пересекающихся прямых для доказательства параллельности.
Важно помнить, что доказательство параллельности прямых требует точности и строгости. Нельзя допускать ошибок при определении углов или рассуждениях о свойствах прямых. При использовании аксиом и теорем геометрии можно убедиться в том, что две прямые действительно параллельны.
Методы доказательства

Для доказательства параллельности прямых существует несколько методов. Рассмотрим основные из них:
| 1. | Метод углов |
| 2. | Метод перпендикулярности |
| 3. | Метод равенства углов |
| 4. | Метод равенства противоположных углов |
Выбор метода зависит от конкретной задачи и ситуации. Нередко при доказательстве параллельности применяются комбинации различных методов, чтобы достичь желаемого результата.
Геометрический способ

Для доказательства параллельности прямых геометрическим способом можно воспользоваться следующими признаками:
- Если две прямые параллельны, то соответствующие углы равны (аксиома параллельных прямых).
- Если четыре прямые пересекаются, образуя одинаковые углы, то две из них параллельны (признак равенства углов).
- Если две прямые пересекаются, образуя вертикальные углы, то они параллельны (признак вертикальных углов).
Используя эти признаки, можно доказать параллельность прямых в геометрии.
Использование углов

| Условие | Описание |
|---|---|
| Углы дополнительныe | Если два угла дополнительныe и равны между собой, то прямые, на которых лежат данные углы, параллельны. |
| Углы смежныe | Если два угла смежныe и их сумма равна 180 градусов, то прямые, на которых лежат данные углы, параллельны. |
Свойства параллельных прямых
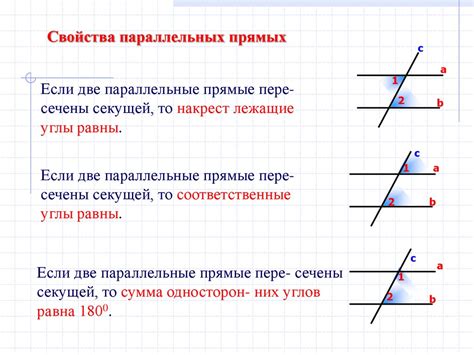
| 1. Если две параллельные прямые пересекаются с третьей прямой, то соответственные углы равны. |
| 2. У параллельных прямых одинаковый угол наклона к эталонной оси. |
| 3. Параллельные прямые имеют одинаковое расстояние между собой на всем протяжении. |
| 4. При пересечении двух параллельных прямых третьей прямой, сумма соответственных углов равна 180 градусам (они смежные). |
Алгебраический подход

Для доказательства параллельности прямых можно воспользоваться алгебраическим подходом, используя уравнения прямых. Если уравнения двух прямых имеют одинаковые коэффициенты наклона, то прямые параллельны. Рассмотрим две прямые, у которых уравнения имеют вид:
| y = k1x + b1 | y = k2x + b2 |
Для доказательства параллельности прямых необходимо убедиться, что коэффициенты наклона k1 и k2 равны друг другу. Если это условие выполняется, то прямые параллельны. Алгебраический подход позволяет эффективно и точно определить параллельность прямых.
Определение параллельности
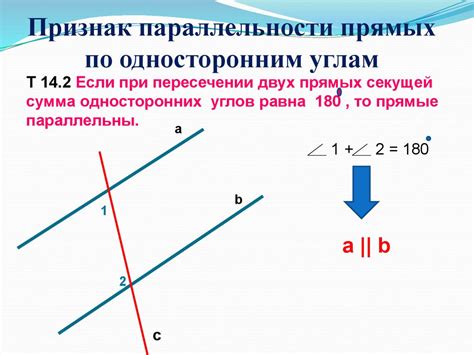
Использование координат
Один из способов доказательства параллельности прямых основан на использовании координат. Для этого необходимо определить координаты точек, через которые проходят прямые. Затем используется уравнение прямой в общем виде, чтобы проверить условие параллельности. Если коэффициенты наклона прямых равны, то они параллельны.
Теоремы и постулаты

Для доказательства параллельности прямых могут применяться следующие теоремы и постулаты:
1. Теорема о параллельных прямых: если две прямые параллельны третьей, то они параллельны между собой.
2. Постулат о параллельности: через точку, не принадлежащую прямой, можно провести только одну прямую, параллельную данной.
3. Теорема о параллельных углах: если две прямые параллельны, то соответственные углы равны.
Проверка на параллельность
Для доказательства параллельности двух прямых необходимо использовать геометрические свойства и теоремы.
- Проверить, что углы между прямыми равны между собой. Если углы двух прямых с параллельными линиями равны, то прямые параллельны.
- Использовать теорему о параллельных прямых, которая утверждает, что если две прямые параллельны третьей прямой, то они параллельны между собой.
- Провести перпендикуляр к одной из прямых и проверить, что он перпендикулярен к другой прямой. Если перпендикуляр к одной прямой также перпендикулярен к другой, то прямые параллельны.
Вопрос-ответ

Как доказать параллельность прямых?
Для доказательства параллельности двух прямых можно воспользоваться несколькими способами. Например, если две прямые параллельны, то у них углы наклона равны. Это значит, что если углы наклона прямых равны, то они параллельны. Также если две прямые пересекаются с третьей прямой и углы между ними равны, то они параллельны. Еще один способ - если две прямые перпендикулярны к одной и той же прямой, то они параллельны. Используйте эти признаки для доказательства параллельности прямых.
Какие признаки параллельности прямых существуют?
Существует несколько признаков, позволяющих определить параллельность прямых. Некоторые из них: если две прямые параллельны, то углы наклона равны; если две прямые пересекаются с третьей прямой и углы между ними равны, то они параллельны; если две прямые перпендикулярны к одной и той же прямой, то они параллельны; если у двух прямых параллельны наклонные, проведенные из одной точки к этим прямым, то прямые также параллельны.
Как использовать признаки для доказательства параллельности двух прямых в геометрии?
Для доказательства параллельности двух прямых в геометрии используйте признаки параллельности, такие как равенство углов наклона, равенство углов при пересечении с третьей прямой, перпендикулярность к одной и той же прямой и равенство наклонных. Применяйте геометрические построения и логические рассуждения, чтобы убедиться в параллельности прямых.
Можно ли доказать параллельность прямых без использования углов?
Да, можно доказать параллельность прямых и без использования углов. Например, если две прямые пересекаются с третьей прямой таким образом, что сумма углов между ними равна 180 градусам, то прямые параллельны. Также можно доказать параллельность прямых, если провести наклонные из одной и той же точки к этим прямым и показать, что они равны. Эти методы позволяют доказать параллельность прямых без использования угловых измерений.
Как доказать параллельность двух прямых?
Для доказательства параллельности двух прямых необходимо использовать характеристики углов между ними. Если углы между прямыми равны, то они параллельны. Например, если две прямые пересекаются, и углы при пересечении одинаковы (например, оба прямые пересекаются с вертикальной), то они параллельны. Также можно использовать параллельные линии на плоскости, перпендикулярные к данным прямым. Если эти линии равны и перпендикулярны одной из прямых, аналогично параллельны другой прямой.



