Поиск экстремума функции – важная задача математического анализа, которая позволяет определить точки максимума и минимума функции. Экстремум – это значения функции, которые оказываются наибольшими или наименьшими среди всех значений, принимаемых функцией в определенной области. Существует несколько способов найти экстремум функции, одним из которых является анализ графика функции.
График функции дает визуальное представление о ее поведении на определенном промежутке. Относительное положение графика, его наклон, точки перегиба и экстремумы могут помочь определить характер зависимости функции от аргумента. Таким образом, график функции является удивительно мощным инструментом для анализа ее поведения и поиска экстремумов.
Как найти максимум функции на графике
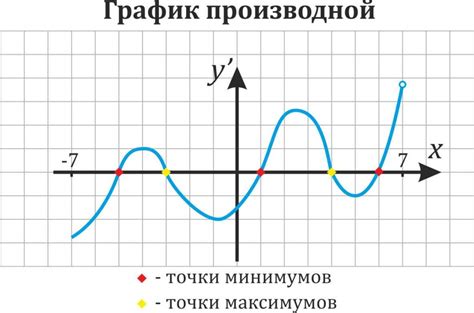
Чтобы найти максимум функции на графике, необходимо обратить внимание на точку, где график функции достигает наивысшего значения. Максимум функции может быть определен как точка, где касательная к графику функции горизонтальна или имеет наклон, указывающий на рост функции.
Для того чтобы найти максимум функции на графике, обратите внимание на точки перегиба и экстремумов, где значение функции достигает максимального значения. Такие точки могут быть ключевыми для определения максимума функции.
Метод графического поиска экстремума

Для поиска минимума функции на графике необходимо найти точку, в которой график функции начинает возрастать после убывания. Это будет точка минимума. Аналогично, для поиска максимума нужно найти точку, в которой график функции начинает убывать после возрастания.
Метод графического поиска экстремума функции может быть полезен для первоначальной оценки точек экстремума, но для более точного определения требуется использование более точных методов, таких как методы дифференциального исчисления.
Определение направления возрастания и убывания функции
Пусть дана функция \( f(x) \). Для определения направления возрастания и убывания функции можно использовать ее график.
1. Направление возрастания функции:
Функция \( f(x) \) возрастает на интервале, если для любых двух точек \( x_1 \) и \( x_2 \) на этом интервале, где \( x_1
На графике функции это выглядит так: график идет вверх с левого края графика к правому краю.
2. Направление убывания функции:
Функция \( f(x) \) убывает на интервале, если для любых двух точек \( x_1 \) и \( x_2 \) на этом интервале, где \( x_1 f(x_2) \).
На графике функции это выглядит так: график идет вниз с левого края графика к правому краю.
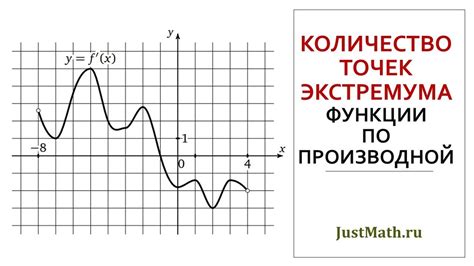
Использование производной для нахождения экстремума
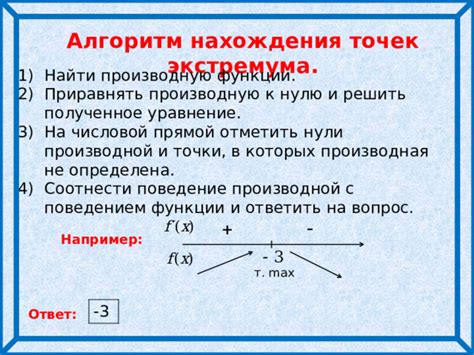
Используя производную, можно анализировать поведение функции вокруг точек экстремума, определять их тип и природу. Этот метод позволяет найти точные значения экстремумов и определить их характер на основе значений производной.
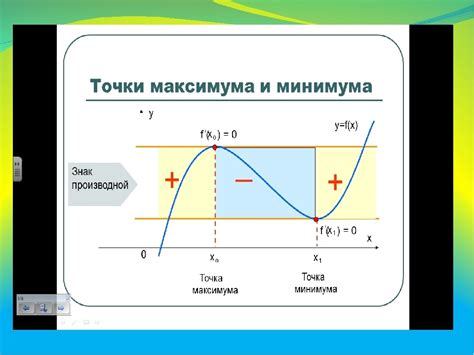
Проверка точки экстремума с помощью второй производной
Пример: если в точке x=2 вторая производная функции f(x) равна 3 (положительна), то это значит, что в точке x=2 функция имеет локальный минимум. Если же вторая производная равна -3 (отрицательна), то это указывает на локальный максимум функции в точке x=2.
Применение метода распространенных экстремумов для исследования функции
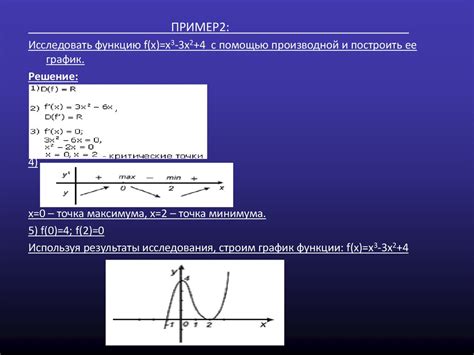
Суть метода заключается в том, что мы аппроксимируем локальный экстремум функции с помощью кривой, которая является гладким продолжением касательной к графику функции в точке экстремума. Таким образом, мы можем определить не только значение экстремума, но и его тип (минимум или максимум).
Для применения метода распространенных экстремумов необходимо уметь находить производные функции и анализировать их поведение в окрестности точки экстремума. Поиск экстремума по графику функции с использованием данного метода позволяет провести глубокий анализ поведения функции вблизи точки экстремума и выявить особенности ее проявления.
Вопрос-ответ

Как можно найти экстремум функции по графику?
Для нахождения экстремума функции по графику необходимо обратить внимание на точки, где касательная горизонтальна (пересекает ось абсцисс). Это могут быть точки максимума или минимума функции. Также стоит обратить внимание на точки, где график меняет свое направление (из возрастающего становится убывающим или наоборот). В этих точках также могут находиться экстремумы функции.
Как определить тип найденного экстремума по графику функции?
Чтобы определить тип экстремума по графику функции, необходимо рассмотреть поведение графика в окрестности найденной точки экстремума. Если график касается оси абсцисс сверху и ниже этой точки, то это может быть точка минимума. Если график касается оси абсцисс снизу и выше этой точки, то это может быть точка максимума. Также стоит анализировать наклон касательной к графику в найденной точке: положительный наклон сверху вниз указывает на минимум, а отрицательный наклон снизу вверх - на максимум.



