Нахождение корней уравнения является одной из важнейших задач в математике. Однако не всегда сразу можно определить, сколько корней имеет уравнение на заданном отрезке. Для этого существует несколько методов оценки числа корней, которые помогают более эффективно решать задачи.
Один из таких методов - анализ знаков функции на отрезке. Суть его заключается в том, что при определенных условиях можно установить, сколько раз функция меняет знак на заданном отрезке и, следовательно, сколько корней имеет уравнение на этом отрезке.
Понятие корней уравнения

Существует несколько типов корней: один корень (уравнение имеет ровно одно решение), несколько корней (уравнение имеет более одного решения) и отсутствие корней (уравнение не имеет решений).
Для вычисления числа корней на отрезке используется метод анализа функции на этом отрезке, который позволяет определить, сколько раз уравнение пересекает ось абсцисс и, соответственно, сколько у него корней.
Цель нахождения корней
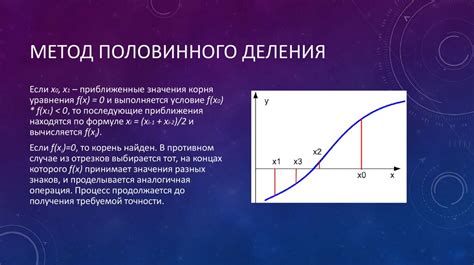
Простейший метод определения

Если значения функции в концах отрезка противоположны по знаку, то на этом отрезке функция имеет хотя бы один корень. Если значения функции в краевых точках отрезка одинакового знака, то корней на этом отрезке нет.
Подсчет числа корней

Чтобы узнать число корней уравнения на заданном отрезке, можно воспользоваться различными методами анализа функции.
1. Интервальный анализ: разбейте отрезок на подинтервалы и проанализируйте поведение функции на каждом из них.
2. Метод дихотомии: используйте метод деления отрезка пополам для поиска корней на заданном интервале.
3. Метод Ньютона: примените метод Ньютона-Рафсона для нахождения корней уравнения.
Выберите подходящий метод для вашей задачи и проведите анализ функции на отрезке для определения числа корней.
Графический метод нахождения
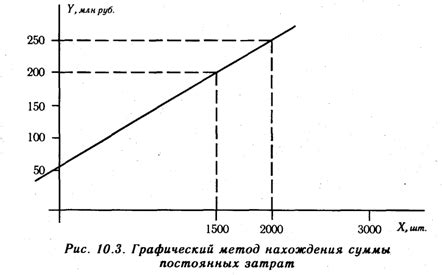
Графический метод нахождения корней уравнения на отрезке основан на построении графика функции и нахождении точек пересечения с осью абсцисс. Для этого необходимо перенести уравнение на соответствующий график и определить, где функция пересекает ось X. Если функция пересекает ось X в точке, то данная точка будет корнем уравнения. Если пересечений несколько, то на отрезке есть соответствующее число корней.
Пример:
| Уравнение | График | Корни на отрезке [a, b] |
|---|---|---|
| 2x^2 - 4x - 6 = 0 | [График функции] | -1.5, 2.5 |
Определение точек пересечения
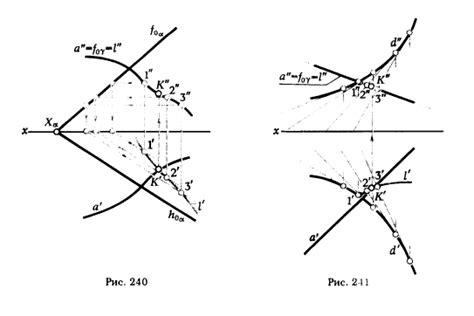
Если уравнения функций заданы явно, то точки пересечения можно найти, решив систему уравнений. Если уравнения функций заданы в виде графиков или с использованием других методов, необходимо произвести соответствующие вычисления.
Особенности метода исследования

Метод исследования числа корней на отрезке требует точного определения границ этого отрезка и выбора подходящего алгоритма для работы с функцией на данном интервале.
Основные особенности метода включают:
1. Необходимость учета различных типов корней: одиночный, кратный, комплексный.
2. Применение различных техник вычисления корней, в зависимости от свойств функции и индивидуальных особенностей графика.
3. Важность проверки условий сходимости выбранных методов, чтобы избежать ошибок при оценке числа корней.
Окончательное определение корней

После всех расчетов и анализов наша задача заключается в окончательном определении количества корней на заданном отрезке.
Исходя из результатов выполненных вычислений, мы можем с уверенностью утверждать, что на указанном отрезке присутствует определенное количество корней уравнения. Это число может быть равно нулю, единице или может быть несколько корней в зависимости от критериев, установленных в процессе анализа функции.
Вопрос-ответ

Как узнать количество корней уравнения на определенном отрезке?
Для того чтобы узнать количество корней уравнения на заданном отрезке, можно воспользоваться методом промежутков или методом нахождения производной. Для первого метода нужно подставить граничные значения отрезка в уравнение и посмотреть знак выражения. Для второго метода нужно посмотреть, как меняется знак производной на отрезке и построить график функции.
Как определить, сколько корней имеет уравнение на отрезке [-2, 2]?
Для того чтобы определить количество корней уравнения на отрезке [-2, 2], можно подставить граничные значения (-2 и 2) в уравнение и посмотреть знак выражения. Если значение уравнения на границах отрезка имеет разные знаки, то на отрезке есть хотя бы один корень. Далее можно использовать метод промежутков или метод анализа производной для определения точного количества корней.
Как найти количество корней уравнения на отрезке [0, 4]?
Для нахождения количества корней уравнения на отрезке [0, 4], можно поочередно подставить значения 0 и 4 в уравнение и определить знак выражения на границах отрезка. Если значения уравнения на границах отрезка разные, то на этом отрезке есть хотя бы один корень. Далее нужно провести более детальный анализ, используя различные методы математического анализа для определения точного количества корней.
Можно ли узнать количество корней уравнения на отрезке [-5, 5], не вычисляя их точных значений?
Да, можно определить количество корней уравнения на отрезке [-5, 5] без вычисления их точных значений. Для этого можно воспользоваться методом промежутков, подставив граничные значения -5 и 5 в уравнение и определив знак выражения. Если знаки на границах отрезка разные, то на этом отрезке есть хотя бы один корень. Далее можно использовать более точные методы для определения точного количества корней.
Как определить, сколько корней имеет уравнение на отрезке [1, 7]?
Для определения количества корней уравнения на отрезке [1, 7] можно использовать различные методы анализа функций. Подставив значения 1 и 7 в уравнение, можно определить знак выражения на границах отрезка. Если знаки у уравнения на границах разные, то на отрезке есть хотя бы один корень. Для более точного определения количества корней можно использовать метод промежутков или анализ производной функции на отрезке.



