Методы Евклида рассматриваются как одни из основополагающих в геометрии, и использование этих методов при построении центра окружности может быть полезным для понимания основных принципов геометрии. Центр окружности - это точка, находящаяся на равном расстоянии от всех точек окружности, и его построение может быть осуществлено различными способами в соответствии с аксиомами Евклида.
В данной статье будет рассмотрено несколько методов построения центра окружности по методам Евклида, которые позволят вам понять основные принципы геометрии и применить их на практике. Каждый из методов будет пошагово описан для лучшего понимания процесса построения центра окружности, а также приведены примеры и иллюстрации для визуализации каждого шага.
Используя подробное руководство по построению центра окружности по методам Евклида, вы сможете на практике увидеть важность аксиом Евклида и освоить основные приемы геометрии, которые могут быть полезны в решении различных математических задач и задач на геометрию.
Основные принципы построения окружности
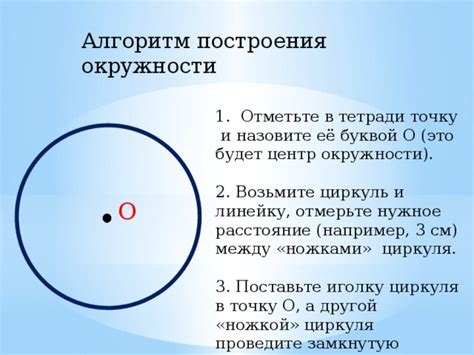
Для построения окружности по методам Евклида необходимо соблюдать следующие основные принципы:
| 1. | Использование циркуля и линейки для построения окружности |
| 2. | Начертание центрального участка, который будет служить центром окружности |
| 3. | Использование подходящей длины радиуса для построения окружности |
| 4. | Тщательное следование шагам построения окружности без допущения ошибок |
История методов Евклида

Методы Евклида оказали огромное влияние на развитие математики и науки в целом. Его работы использовались в течение многих столетий как основа для изучения геометрии и применения ее в различных областях знаний.
Необходимые инструменты и материалы

Для построения центра окружности по методам Евклида вам понадобятся следующие инструменты и материалы:
- Линейка
- Карандаш
- Циркуль
- Доска или лист бумаги
- Компас
- Угольник
Шаги построения центра окружности
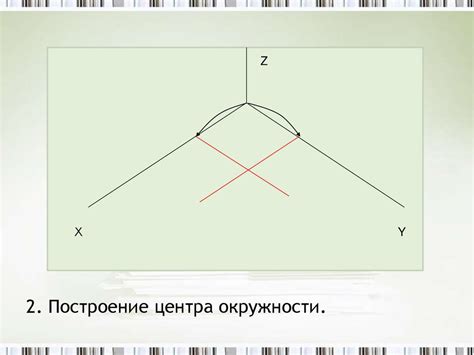
1. Построить любые две хорды окружности.
2. Найти середины этих хорд и провести через них прямую.
3. Найти точку пересечения этой прямой с окружностью - это и будет центр окружности.
Использование угломера для точных измерений

Для использования угломера следуйте простым шагам:
- Убедитесь, что угломер правильно установлен и не искажает измерения.
- Поместите угломер на точку центра окружности и выровняйте его.
- Поверните угломер до того момента, когда он покажет угол в 60 градусов.
- Проверьте точность измерения и убедитесь, что угол действительно равен 60 градусов.
После того, как угол в 60 градусов точно измерен, вы можете продолжить построение центра окружности согласно методам Евклида.
Применение уравнений Эвклида для вычислений

В построении центра окружности по методам Евклида широко применяются уравнения, которые позволяют точно определить положение центра. Для этого необходимо использовать формулы, основанные на геометрии и математике. Эвклидовы уравнения позволяют рассчитать координаты центра окружности и радиус, что позволяет закрепить конструкцию точно и надежно.
Важно помнить, что правильное использование уравнений Эвклида требует точности и внимательности при проведении вычислений. Необходимо завершить все шаги конструкции, прежде чем приступить к расчетам, чтобы избежать ошибок и получить достоверный результат.
Точность и форма окружности по методам Евклида
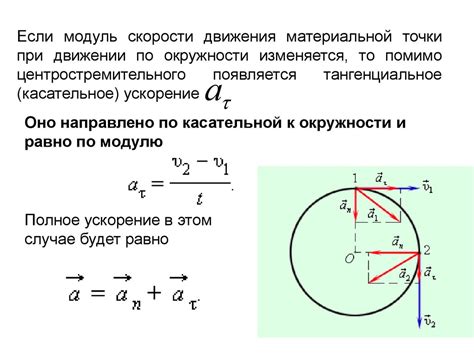
При использовании методов Евклида для построения центра окружности необходимо уделить особое внимание точности определения центральной точки и радиуса. Это обеспечит точную форму окружности и минимизирует возможные ошибки.
Важно помнить, что точность окружности по методам Евклида зависит от точности и последовательности выполнения шагов по построению. Тщательное следование инструкциям и внимание к деталям позволят получить идеальную форму окружности, соответствующую заданным параметрам.
Примеры построения центра окружности на плоскости
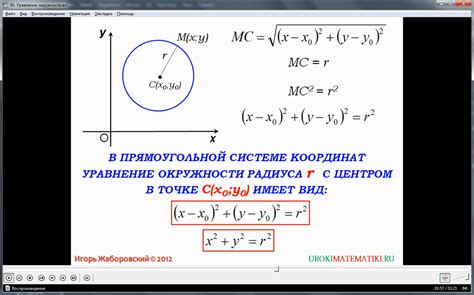
Ниже приведены примеры построения центра окружности на плоскости с помощью методов Евклида:
- Используя перпендикулярность: проведите два перпендикуляра к диаметру окружности. Их точка пересечения будет центром окружности.
- С помощью радиуса: проведите два хорда окружности и постройте их серединный перпендикуляр. Точка пересечения с центром окружности будет находиться на расстоянии радиуса от каждой из хорд.
- Метод тангенций: проведите две касательные к окружности из точек пересечения хорды с окружностью. Точка пересечения касательных будет являться центром окружности.
Сферические методы Евклида и их применение

Применение сферических методов Евклида широко встречается в астрономии, геодезии, навигации и других областях, где необходимо работать с объектами на поверхности сферы.
- Одним из примеров применения сферических методов является нахождение расстояния между двумя точками на Земле с использованием долготы и широты этих точек.
- Другим примером может служить вычисление углов между небесными объектами на небесной сфере в астрономии.
Особенности построения окружности на различных поверхностях

На сфере, например, окружность представляет собой большой круг, который является ограниченным по длине и имеет особенность касаться всех точек экватора. Для построения окружности на сфере используются геодезические методы и формулы, учитывающие кривизну поверхности.
На эллипсоиде построение окружности требует учета сложной формы поверхности и использования специальных алгоритмов. Окружность на эллипсоиде может быть представлена как параллель окружности на плоскости, но с учетом изменения размера и формы.
Вопрос-ответ

Как построить центр окружности по методу Евклида?
Для построения центра окружности по методу Евклида следует провести хорду, затем построить две хорды. Через эти две хорды провести прямую и найти их точку пересечения - это и будет центр окружности.
Как выбрать правильные точки для построения центра окружности по методу Евклида?
Для выбора правильных точек следует провести хорду, а затем взять любые две точки на этой хорде. После этого провести через эти точки прямую и найти их точку пересечения - она будет центром окружности.
Можно ли построить центр окружности по методу Евклида без проведения хорды?
Нет, для использования метода Евклида необходимо сначала провести хорду, а затем построить две хорды и найти их точку пересечения, которая будет центром окружности.
Какую роль играют хорда и пересечение прямых при построении центра окружности по методу Евклида?
Хорда служит отправной точкой для построения центра окружности по методу Евклида. Проведя две хорды и через них прямую, можно найти точку их пересечения, которая будет являться центром окружности.
Какой алгоритм построения центра окружности по методу Евклида наиболее эффективен для начинающих?
Для начинающих наиболее эффективным может быть алгоритм, который заключается в проведении хорды, затем построении двух хорд и нахождении их точки пересечения. Такой метод является понятным и наглядным для новичков.



