Перпендикулярность – одно из важнейших понятий в геометрии, которое означает взаимное расположение линий, плоскостей или отрезков под прямым углом. В данной статье рассмотрим различные способы определения перпендикулярности между двумя плоскостями.
Первый способ – проверка угла между нормалями плоскостей. Для этого необходимо найти нормали к каждой из плоскостей и проверить их скалярное произведение. Если скалярное произведение нормалей равно нулю, то плоскости перпендикулярны.
Добавим еще один метод: если векторы, параллельные плоскостям, не являются коллинеарными, то плоскости также будут перпендикулярными. Эти и другие методы позволяют более полно представить себе взаимное расположение плоскостей в пространстве.
Метод с использованием векторов
Для определения перпендикулярности двух плоскостей можно воспользоваться векторным методом. Пусть заданы два уравнения плоскости:
\(ax + by + cz + d_1 = 0\) и \(a'x + b'y + c'z + d_2 = 0\), где \(n = (a, b, c)\) и \(n' = (a', b', c')\) - нормальные векторы плоскостей соответственно.
Плоскости перпендикулярны, если их нормальные векторы коллинеарны, то есть если их векторное произведение равно нулевому вектору: \(n \times n' = 0\).
| Плоскость 1: | \(ax + by + cz + d_1 = 0\) | Нормальный вектор: | \(n = (a, b, c)\) |
| Плоскость 2: | \(a'x + b'y + c'z + d_2 = 0\) | Нормальный вектор: | \(n' = (a', b', c')\) |
Определение направляющих векторов
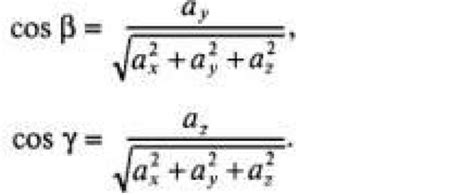
Направляющими векторами для плоскости, заданной уравнением Ax + By + Cz + D = 0, будут векторы, координаты которых равны (A, B, C). Таким образом, если даны две плоскости с уравнениями А1x + В1y + C1z + D1 = 0 и А2x + В2y + C2z + D2 = 0, их направляющие векторы будут (А1, В1, C1) и (А2, В2, C2) соответственно.
Вычисление скалярного произведения
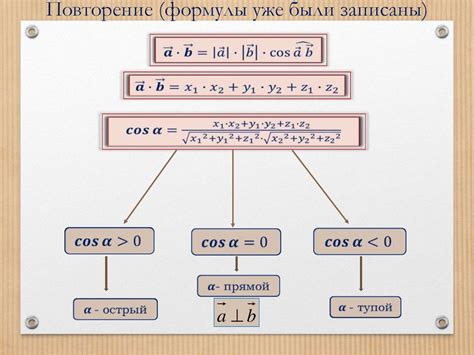
Метод с использованием нормалей
Для определения перпендикулярности двух плоскостей можно воспользоваться нормалями к этим плоскостям. Нормалью к плоскости называется прямая, перпендикулярная к данной плоскости. Если направления нормалей к двум плоскостям перпендикулярны, то и сами плоскости будут перпендикулярны.
- Найти уравнения плоскостей в общем виде.
- Найти уравнения нормалей к плоскостям.
- Проверить, что нормали перпендикулярны друг к другу.
- Если направления нормалей перпендикулярны, то плоскости тоже перпендикулярны.
Нахождение нормалей к плоскостям
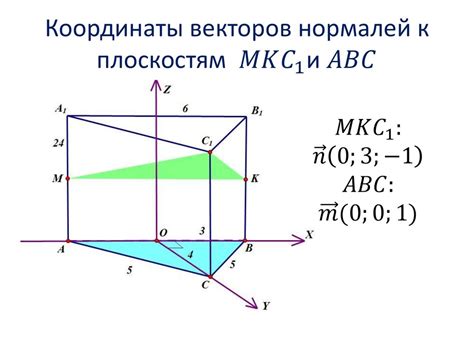
Для определения нормалей к плоскостям необходимо знать уравнение плоскости. Нормаль к плоскости определяется как вектор, перпендикулярный этой плоскости. Для уравнения плоскости в общем виде Ax + By + Cz + D = 0 нормальный вектор будет иметь компоненты (A, B, C).
Если уравнение плоскости задано в виде Ax + By + Cz = D, то нормальный вектор будет иметь компоненты (A, B, C).
Таким образом, для определения нормалей к плоскостям необходимо лишь взять коэффициенты перед переменными в уравнении плоскости.
Сравнение углов нормалей
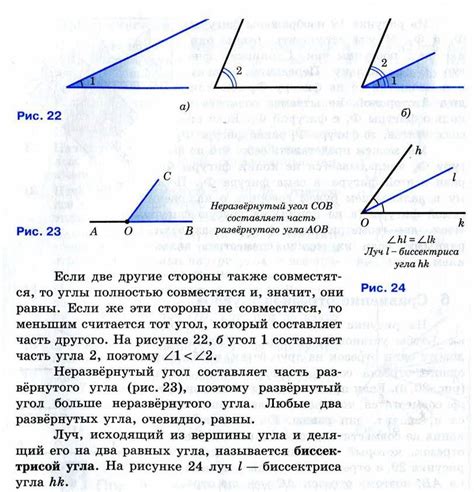
Для определения перпендикулярности между двумя плоскостями можно сравнивать углы, которые образуют нормали к этим плоскостям. Если углы нормалей равны, то плоскости перпендикулярны друг другу.
Угол между нормалями к плоскостям можно вычислить с помощью скалярного произведения векторов нормалей: если скалярное произведение равно нулю, то углы нормалей равны, и плоскости перпендикулярны.
Метод с использованием коэффициентов уравнений плоскостей

Для определения перпендикулярности между двумя плоскостями можно воспользоваться коэффициентами их уравнений. Для этого необходимо рассмотреть коэффициенты обеих плоскостей и проверить выполнение условия перпендикулярности:
- Пусть уравнение первой плоскости имеет вид Ax + By + Cz + D1 = 0, а уравнение второй плоскости - Ax + By + Cz + D2 = 0.
- Плоскости перпендикулярны, если сумма произведений коэффициентов A1A2 + B1B2 + C1C2 равна нулю.
- Проведя соответствующие вычисления, можно установить, являются ли заданные плоскости перпендикулярными друг другу.
Нахождение коэффициентов плоскостей
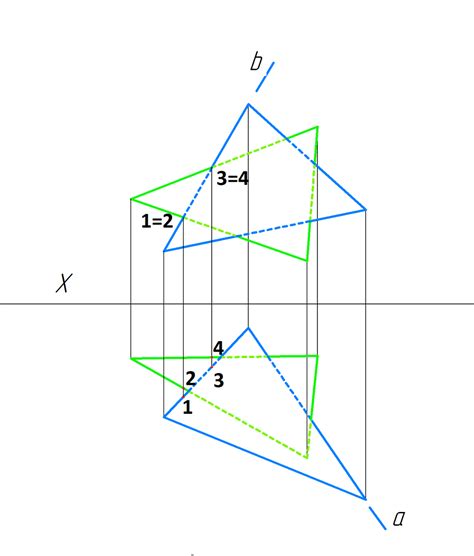
Сопоставление коэффициентов
Следовательно, для проверки перпендикулярности двух плоскостей необходимо вычислить указанное значение и убедиться, что оно равно нулю. Если значение равно нулю, то плоскости перпендикулярны друг другу.
Вопрос-ответ

Как определить перпендикулярность между двумя плоскостями?
Перпендикулярность между двумя плоскостями можно определить с помощью критерия ортогональности плоскостей. Для этого необходимо проверить, что векторы нормалей к плоскостям ортогональны между собой, то есть их скалярное произведение равно нулю. Если проекция одной нормали на другую равна нулю, то плоскости перпендикулярны.
Можно ли определить перпендикулярность между плоскостями без использования векторов?
Да, перпендикулярность между плоскостями можно определить с помощью уравнений плоскостей. Для этого необходимо записать уравнения данных плоскостей и проверить их коэффициенты при переменных. Если коэффициенты при переменных в уравнениях плоскостей одни и те же, то плоскости перпендикулярны.
Какова геометрическая интерпретация перпендикулярности двух плоскостей?
Перпендикулярность двух плоскостей обозначает, что они пересекаются под прямым углом. Геометрически это означает, что направление одной плоскости ортогонально направлению другой плоскости, что в свою очередь гарантирует, что прямые, строимые в каждой плоскости и перпендикулярные к аналогичной прямой из другой плоскости, будут образовывать прямой угол.



