Тригонометрия – одна из основных математических дисциплин, которая изучает отношения между сторонами и углами в треугольниках. Важным инструментом в решении различных задач, связанных с треугольниками, являются синусы, косинусы и тангенсы углов. Синус угла – это величина, определяемая отношением противолежащей стороны к гипотенузе в прямоугольном треугольнике. Как же можно использовать синусы для определения сторон треугольника?
В данной статье мы подробно рассмотрим методы, с помощью которых можно найти стороны треугольника по заданным значением синусов углов. Мы разберем, как использовать тригонометрические функции и формулы для нахождения искомых сторон, а также рассмотрим примеры решения задач на нахождение сторон треугольника по синусу.
Определение главной формулы

Для того, чтобы найти сторону треугольника по синусу, можно использовать следующую формулу:
- Для стороны a: a = c * sin(A) / sin(C)
- Для стороны b: b = c * sin(B) / sin(C)
- Для стороны c: c = a * sin(C) / sin(A) = b * sin(C) / sin(B)
Здесь a, b, c - стороны треугольника, A, B, C - соответствующие углы, sin - синус угла. Данная формула позволяет находить отсутствующие стороны треугольника, зная синус угла и другие стороны.
Как найти первый угол через синус
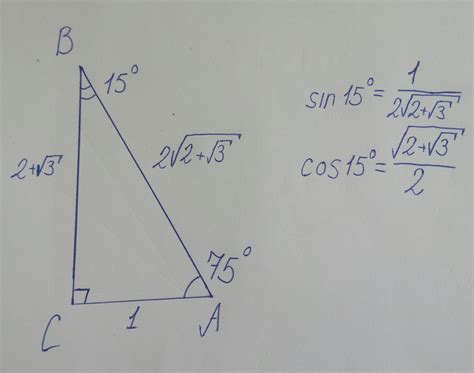
- Для начала найдите значение синуса угла. Например, sin(A) = 0.5
- Затем примените обратную функцию синуса к данному значению. Для примера: A = arcsin(0.5)
- Результатом будет значение угла A в радианах. Чтобы получить угол в градусах, используйте формулу: A в градусах = A в радианах * 180 / π
Шаги по нахождению второго угла
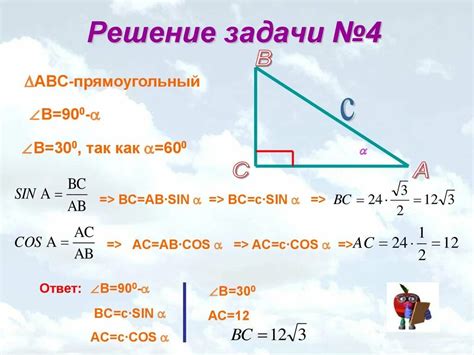
Шаг 2: Найдите значение угла, соответствующего найденному значению синуса, используя обратную функцию arcsin. Например, угол a = arcsin(sin(a)).
Шаг 3: Найдите второй угол треугольника, вычитая из суммы углов треугольника (180 градусов) найденный угол.
Примеры вычисления стороны треугольника
Для примера возьмем треугольник ABC, в котором известен угол CAB и его синус, а также сторона BC.
| Дано | Известно |
|---|---|
| Синус угла CAB | sin(CAB) = 0.8 |
| Сторона BC | BC = 5 см |
Теперь можем использовать формулу sin(CAB) = BC / AB, чтобы найти сторону AB:
sin(CAB) = BC / AB
0.8 = 5 / AB
AB = 5 / 0.8 = 6.25 см
Таким образом, сторона AB треугольника ABC равна 6.25 см.
Использование обратного синуса для нахождения третьего угла

Например, пусть у нас есть треугольник ABC, где AB=5, AC=3 и sin(A)=0.6. Чтобы найти угол A, мы можем использовать формулу:
A = asin(AC* sin(A) / AB) = asin(3 * 0.6 / 5) ≈ 0.6435 радиан или ≈ 36.87 градусов.
Рекомендации и советы по поиску стороны треугольника
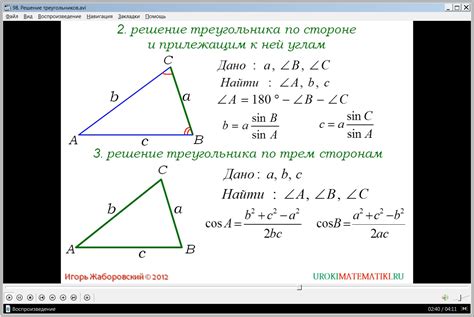
1. Внимательно изучите задачу и определите, какая сторона треугольника вам нужна: противолежащая, прилежащая или гипотенуза.
2. Проверьте, известен ли вам угол треугольника и значение синуса этого угла.
3. Используйте формулу sin(A) = a/c (для противолежащей стороны), sin(B) = b/c (для прилежащей стороны) или sin(C) = a/b (для гипотенузы), чтобы найти нужное значение стороны.
4. Проверьте правильность вычислений и внимательно оцените полученный результат.
Следуя этим советам, вы сможете успешно находить стороны треугольника по заданным синусам углов.
Вопрос-ответ

Как найти сторону треугольника, если известен синус угла?
Для определения стороны треугольника по синусу угла можно воспользоваться формулой синуса: сторона = (длина другой стороны) / sin(известный угол). Например, если известен угол и длина одной из сторон, можно найти с помощью синуса длину противолежащей стороны.
Как найти сторону треугольника, если дан угол и синус этого угла?
Если известен угол и его синус, то можно использовать соответствующее соотношение: сторона = (длина другой стороны) / sin(известный угол). Данная формула позволяет найти длину стороны, противолежащей известному углу.
Какие формулы использовать для нахождения стороны треугольника по синусу?
Для определения стороны треугольника по синусу угла можно использовать формулу: сторона = (длина другой стороны) / sin(известный угол). Эта формула позволяет вычислить длину стороны, противолежащей известному углу, если известны длина другой стороны и величина синуса угла.



