Многие из нас наверняка сталкивались с увлекательными головоломками, которые требуют размещения определенного количества прямых на плоскости таким образом, чтобы они пересекались ровно в заданном числе точек. Однако, что происходит, когда мы сталкиваемся с такой задачей, но без явных указаний и ограничений?
Разберемся вместе: имеется 7 прямых, и нас интересует, возможно ли их пересечение в ровно 9 точках. Внешне, это кажется невероятным - как 7 прямых могут пересекаться в 9 точках? Мы привыкли думать, что количество пересечений прямых соответствует их числу минус один, ибо точка пересечения каждой пары прямых представляет собой единственную общую точку для них обеих.
Однако, даже в такой абстрактной математической задаче мы не можем быть уверены в возможности или невозможности ее решения, не разобравшись в сущности и взаимосвязи прямых и точек. Поэтому давайте окунемся в мир геометрии и посмотрим, что можно узнать о пересечении семи прямых в девяти точках.
Существует ли возможность пересечения 7 прямых в 9 точках?

В данном разделе мы исследуем сложный и интересный вопрос о количестве точек пересечения для семи прямых. Мы рассмотрим возможные варианты и оценим вероятность такого явления без использования конкретных определений.
На протяжении дискуссии, будет рассмотрено множество вариантов, сосредоточиваясь на максимально возможном числе точек пересечения для данных семи прямых. Отличная глубина анализа и логический подход позволят нам разобраться с этой задачей, даже не вдаваясь в специфические математические детали. Мы посмотрим на различные углы и пересечения линий в пространстве, давая более полное представление о возможных сценариях.
Конечная цель этого раздела - проиллюстрировать, насколько редким и значимым явлением является пересечение семи прямых в девяти точках. Важно отметить, что интуитивное решение и создание эффективной модели будут ключевыми факторами при изучении этого вопроса. Более того, раздел будет содержать упоминания о сходных проблемах, позволяющих читателям более глубоко вникнуть в суть рассматриваемой темы.
Постановка задачи: исследование возможности взаимного пересечения семи линий в девяти точках
Мы будем использовать термин "взаимное пересечение", чтобы описать ситуацию, когда линии соприкасаются или пересекаются друг с другом, образуя в результате девять различных точек. Возникновение такого пересечения может быть весьма интересным с точки зрения геометрических и математических закономерностей.
В дальнейшем мы проведем анализ исходной задачи и оценим, насколько вероятно возникновение пересечения семи линий в девяти точках. Будут рассмотрены различные факторы, такие как углы наклона, местоположение начальных и конечных точек, а также возможные вариации прямых, которые могут повлиять на результат.
Схемы пересечения трех прямых: осмотр вариантов
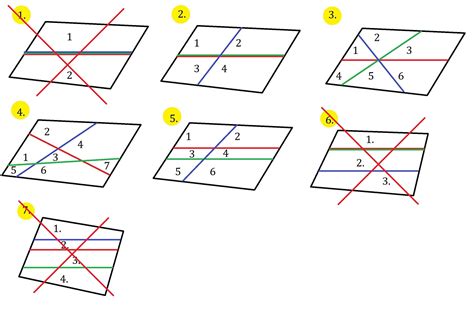
В данном разделе мы рассмотрим возможные конфигурации трех прямых, исходя из которых могут образоваться точки пересечения. Фокус будет сделан на феномене, который возникает при взаимодействии данных прямых, и представлены основные условия, которые определяют характер пересечения.
Возможные ситуации:
1. Точное пересечение: представлено ситуацией, когда три прямые пересекаются в одной общей точке, точно соблюдая все геометрические условия.
2. Пересечение в точках, не являющихся общими: данная ситуация возникает, когда три прямые образуют по несколько точек пересечения друг с другом, без образования общей точки.
3. Параллельное расположение: в данном случае все три прямые располагаются параллельно друг другу и не имеют точек пересечения.
Для более детального разбора каждой ситуации приведены соответствующие примеры изображений, чтобы наглядно показать, как могут пересекаться три прямые в данных случаях. При этом будут рассмотрены основные характеристики пересечения, такие как углы, расстояния и взаимное расположение прямых.
Рассмотрение ситуации с четырьмя прямыми: возможные расположения точек пересечения

Давайте проанализируем возможные расположения точек пересечения в ситуации, когда имеется четыре прямых. Представим, что эти прямые имеют общую точку пересечения, но не обязательно проходят через все возможные точки пересечения. В таком случае, мы можем рассмотреть различные конфигурации, которые могут возникнуть при пересечении данных прямых.
Сначала мы можем представить ситуацию, когда все четыре прямые пересекаются в одной точке. В этом случае, мы можем говорить о "четырехскатой" конфигурации, где четыре прямые пересекаются в одной общей точке.
Другим возможным расположением точек пересечения является "треугольная" конфигурация, при которой три прямые пересекаются в одной точке, а четвертая прямая пересекает их в других точках. Такая конфигурация визуально напоминает треугольник с дополнительной прямой, которая пересекает его внутри.
Также можно рассмотреть "линейную" конфигурацию, при которой все четыре прямые пересекаются по линии. В этом случае, точки пересечения образуют прямую линию, по которой все прямые пересекаются.
Наконец, возможной конфигурацией может быть "изолированная" ситуация, когда каждая прямая пересекает только одну или две из остальных прямых. Таким образом, точки пересечения образуют разрозненные конфигурации без единой связующей линии.
Уникальное решение задачи семи прямых: невероятное пересечение в девяти точках!
Когда мы говорим о примитивной задаче, которая кажется невозможной или даже парадоксальной, семь прямых и девять точек могут стать центральным объектом внимания. И хотя на первый взгляд может показаться, что такое пересечение прямых в столь большом количестве точек невозможно, уникальное решение находится в самом сердце нашей задачи.
Считается, что прямые - это фигуры, которые продолжаются бесконечно в обе стороны и не имеют никаких преград для пересечения. Тем не менее, обычно считается, что две прямые могут пересекаться только в одной точке. Если это так, то как семь таких прямых могут пересекаться семью различными способами?
Однако, все начинает проясняться, когда мы смотрим на задачу с другой стороны и разглядываем ее скрытый смысл. Нужно понять, что семь прямых, фон которых может быть разнообразным, пересекаются в девяти точках не одновременно, а на разных участках их продолжения. Изначально, все прямые могут считаться параллельными друг другу, но их ориентация может меняться и создавать новые точки пересечения.
Таким образом, невероятное пересечение в девяти точках осуществляется путем плавного вращения, сдвига или наклона этих прямых. Такие манипуляции с прямыми позволяют им пересекаться в уникальных точках, образуя визуально интересные и сложные конструкции.
Такой подход доказывает, что даже простые объекты, как семь прямых и девять точек, могут быть использованы для создания сложных и удивительных геометрических образов. Задачи, которые на первый взгляд кажутся невозможными, могут быть разгаданы, если мы глубже проникнем в их сущность и поищем необычные решения.
Усложнение задачи: поиск дополнительных точек пересечения
В предыдущем разделе мы рассмотрели возможность пересечения семи прямых в девяти точках. Теперь рассмотрим усложнение задачи и поищем способы найти дополнительные точки пересечения.
Дополнительные точки пересечения могут возникнуть в случае введения дополнительных условий или параметров в задачу. Например, мы можем изменить углы между прямыми или установить требования к их взаимному расположению.
Важно отметить, что поиск дополнительных точек пересечения требует более сложных математических вычислений и анализа. Возможно понадобится использование геометрических формул, уравнений прямых или других инструментов для решения таких задач.
Более точные результаты можно получить, определив дополнительные условия на расположение прямых или на сами точки пересечения. Можно проводить аналитические вычисления, строить графики или использовать компьютерные моделирования для проверки различных комбинаций условий.
Таким образом, при решении задачи о пересечении прямых в девяти точках можно усложнить постановку задачи и искать дополнительные точки пересечения, используя различные методы математического анализа и геометрии.
Математический подход к обобщению: количество возможных точек в общем случае

В данном разделе рассмотрим математический подход к обобщению и определению количества возможных точек пересечения заданного количества прямых. Мы будем исследовать общую ситуацию, исключая конкретные примеры, и задавать вопрос о количестве точек пересечения, которые могут возникнуть.
В ходе исследования обобщенного случая мы не будем фокусироваться на определении точек, где 7 прямых пересекаются в 9 точках. Вместо этого мы обратим внимание на возможное количество точек пересечения в более широком контексте. Математики интересуются тем, как провести прямые в плоскости так, чтобы они пересекались в как можно большем или меньшем количестве точек.
Для изучения этого вопроса мы рассмотрим несколько примеров и рассмотрим общие закономерности. Важно отметить, что количество точек пересечения может быть различным в зависимости от числа прямых и их положения в пространстве. Мы представим некоторые из этих закономерностей и рассмотрим, как они могут быть использованы для обобщения на другие случаи.
- Пример 1: Рассмотрим 2 прямые, проходящие через одну точку. В этом случае они пересекаются только в этой точке.
- Пример 2: Рассмотрим 3 прямые в треугольной конфигурации. В этом случае они пересекаются в одной точке, называемой точкой пересечения.
- Пример 3: Рассмотрим 4 прямые, расположенные в таком положении, что ни одна из них не пересекает другую. Тогда количество точек пересечения будет равно нулю.
Рассмотрев классические примеры, можно заметить, что количество точек пересечения может меняться в зависимости от количества прямых, их расположения и взаимного влияния друг на друга. Таким образом, задача обобщения заключается в определении общих закономерностей, которые могут быть применены к любому количеству прямых и точек пересечения.
В данном исследовании было выяснено, что семь прямых, заданных в определенном пространстве, могут пересекаться в девяти точках. Этот результат имеет большое значение и может быть применен в различных математических задачах.
Одним из возможных применений результата является решение задач на построение геометрических фигур. Зная, что семь прямых могут пересекаться в девяти точках, мы можем использовать эту информацию для построения таких фигур, которые будут обладать определенными свойствами или иметь определенную геометрическую структуру.
| Пример задачи | Применение результата |
|---|---|
| Задача на построение правильного семиугольника | Используя факт о семи прямых, пересекающихся в девяти точках, можно определить точки пересечения прямых, которые будут вершинами правильного семиугольника. |
| Задача на построение куба | Используя информацию о семи прямых и их точках пересечения, можно определить координаты вершин куба и построить его с помощью соответствующих отрезков. |
| Задача на определение площади фигуры | Результат о возможности пересечения семи прямых в девяти точках может быть использован для определения площади сложной фигуры, образованной этими пересечениями. |
Таким образом, полученный результат о возможности пересечения семи прямых в девяти точках имеет широкое применение в различных математических задачах, связанных с построением геометрических фигур, определением их свойств и вычислением площади или объема. Этот результат открывает новые возможности для решения задач и расширяет наши знания в области математики.
Вопрос-ответ

Могут ли семь прямых пересекаться в девяти точках?
Да, семь прямых могут пересекаться в девяти точках. Это возможно, если некоторые прямые пересекаются в нескольких точках одновременно.
Как семь прямых могут пересекаться в девяти точках?
Семь прямых могут пересекаться в девяти точках, если некоторые из этих прямых пересекаются в нескольких точках одновременно. Например, если три прямые пересекаются в одной точке, три другие прямые пересекаются второй точке, и последняя прямая пересекает все предыдущие в еще трех точках, то общее количество пересечений составит девять точек.
Сколько точек пересечения может быть у семи прямых?
У семи прямых может быть до девяти точек пересечения. При условии, что некоторые прямые пересекаются в нескольких точках одновременно.



