Число 1 – это самое простое и особенное числовое значение в мире математики. Однако, оно отличается от других целых чисел тем, что не является квадратом никакого целого числа. Это связано с особенностями самой природы математических операций и свойствами чисел.
Чтобы быть квадратом целого числа, число должно быть результатом умножения целого числа на само себя. Однако, умножение любого целого числа на себя дает результат, отличный от 1. Таким образом, число 1 не может быть представлено в виде квадрата целого числа.
Причины неравенства

1. Определение квадратного числа предполагает, что оно является квадратом некоторого целого числа, то есть результатом возведения целого числа в квадрат. При этом квадратный корень из числа 1 равен 1, что означает, что число 1 является квадратом только самого себя, однако не является квадратом отличного от нуля целого числа.
2. Другими словами, для того чтобы число было квадратом целого числа, его квадратный корень должен быть целым числом. В случае числа 1, его квадратный корень равен 1, что не отвечает условию быть целым числом, отличным от нуля.
Отсутствие двух различных множителей

Целое число можно представить в виде произведения двух других целых чисел, которые называются множителями. Для того чтобы число было квадратом целого числа, существует два одинаковых множителя. Например, квадрат целого числа 9 можно представить как 3 * 3.
Однако число 1 единственно в своем роде и не имеет возможности быть представлено как произведение двух различных целых чисел. Поэтому число 1 не является квадратом целого числа, так как не существует двух различных множителей, дающих результат 1.
Математический аспект

Квадратом целого числа называется число, полученное умножением целого числа на само себя. Например, квадрат числа 4 равен 16, так как 4 умноженное на 4 равно 16. Однако при умножении числа 1 на само себя, результат остается равен 1, а не увеличивается до другого целого числа. Поэтому число 1 не является квадратом целого числа. Квадратами целых чисел могут быть только числа, большие 1, которые при умножении на себя дают новое целое число.
Квадрат числа 1 равен 1
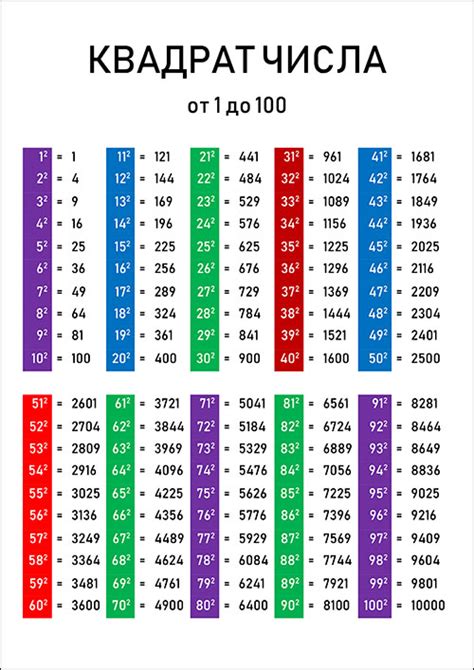
Так как число 1 умноженное само на себя равно 1, то квадрат числа 1 равен 1.
Свойства квадратов

1. Если число является квадратом целого числа, то оно всегда положительно (кроме случая с нулем).
2. Квадрат любого целого числа является неотрицательным числом.
3. Четные квадраты всегда дают четные числа, а нечетные - нечетные.
4. Число 1 не является квадратом целого числа, так как единица умноженная на себя равна единице, а не нулю.
Четность и нечетность
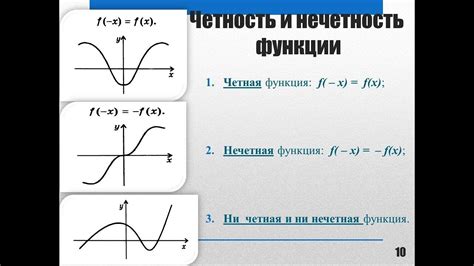
Сравнение с другими числами

В отличие от чисел 4, 9, 16 и других, число 1 не может быть представлено как квадрат целого числа. Для того чтобы 1 было квадратом, оно должно быть результатом умножения на себя же какого-то целого числа. Однако, такого целого числа не существует, что делает число 1 единственным числом, не являющимся квадратом целого числа.
Различия от чисел 4, 9 и т.д.
Основное различие между числами 1 и 4, 9 заключается в том, что 1 не обладает свойством быть квадратом целого числа. Несмотря на то, что 1 является целым числом и может быть представлено в квадратной форме 1x1, согласно определению квадрата целого числа такое число должно иметь два одинаковых множителя.
Таким образом, число 1 не является квадратом целого числа, в отличие от чисел 4, 9 и других, которые можно представить в виде квадратов целых чисел.
Изучение функций

Изучение функций в математике позволяет анализировать и описывать различные процессы и зависимости между переменными. Область применения функций включает множество дисциплин, начиная от алгебры и геометрии, и заканчивая физикой и экономикой.
Изучение функций позволяет решать разнообразные задачи, включая определение максимумов и минимумов, построение графиков, нахождение корней уравнений, и многое другое. Знание функций является фундаментальным для понимания многих математических и физических концепций.
Применение квадратных корней
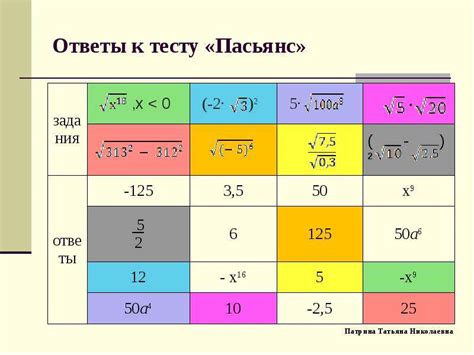
Квадратные корни широко используются в различных областях математики и физики: они помогают решать уравнения, вычислять площади и объемы фигур, находить средние значения и многое другое. Как правило, корни применяются при работе с квадратами и квадратными уравнениями.
Квадратный корень из отрицательного числа не имеет значения в области действительных чисел, но он может быть определен в комплексной плоскости, что находит свое применение в алгебре и физике.
Вопрос-ответ

Почему число 1 не является квадратом целого числа?
Число 1 не является квадратом целого числа, потому что квадрат целого числа определяется как произведение числа на само себя. То есть, число x является квадратом целого числа, если существует такое целое число y, что x = y * y. Однако, если взять целое число y = 1, то 1 * 1 = 1, что показывает, что число 1 является квадратом самого себя, но это уже тривиальный случай, так как любое число, умноженное на 1, равно самому числу. Поэтому, чтобы число считалось квадратом целого числа, в определении требуется, чтобы произведение было равно числу, но при этом множитель был бы не равен самому числу.
Как можно формально доказать, что число 1 не является квадратом целого числа?
Для доказательства того, что число 1 не является квадратом целого числа, можно предположить, что существует некоторое целое число y, такое что y * y = 1. Предположим, что y больше нуля (в случае y y = sqrt(1) = 1. Таким образом, получаем, что y = 1. Но в данном случае получается, что y = 1, что означает, что число 1 является квадратом самого себя. Однако, это не удовлетворяет условию определения квадрата целого числа, которое требует, чтобы множитель отличался от самого числа, т.е. чтобы x ≠ y. Следовательно, число 1 не является квадратом целого числа.



