Пересечение двух отрезков - один из основных кейсов в геометрии, который вызывает много вопросов и дискуссий. Одним из возможных вариантов пересечения является случай, когда луч становится пересечением двух отрезков. Но насколько это возможно в реальных геометрических конструкциях?
Луч – это бесконечно длинное линейное образование, имеющее начало и направление. А отрезок – это конечный отрезок прямой линии, который имеет начальную и конечную точки. Пытаясь визуализировать ситуацию, где луч становится пересечением двух отрезков, мы сталкиваемся с интересными аспектами геометрии и логики.
Как определить пересечение двух отрезков
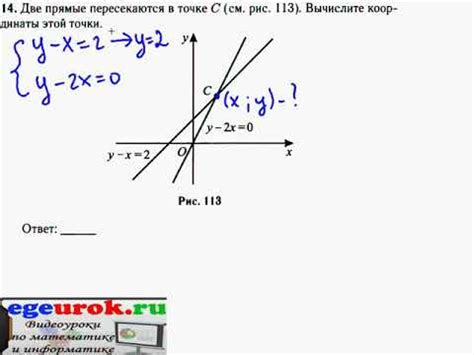
1. Параметрическое уравнение отрезка
Для каждого отрезка задаются параметрические уравнения вида:
Отрезок 1: x1 = x1start + a1(t), y1 = y1start + b1(t)
Отрезок 2: x2 = x2start + a2(u), y2 = y2start + b2(u)
2. Поиск пересечения
Определить пересечение двух отрезков можно путем решения системы уравнений для параметров уравнений отрезков t и u:
x1(t) = x2(u)
y1(t) = y2(u)
3. Проверка на принадлежность отрезков
Итоговые значения параметров t и u проверяются на принадлежность отрезкам, чтобы определить, пересекаются ли отрезки внутри своих диапазонов значений параметров.
Система координат для расчетов
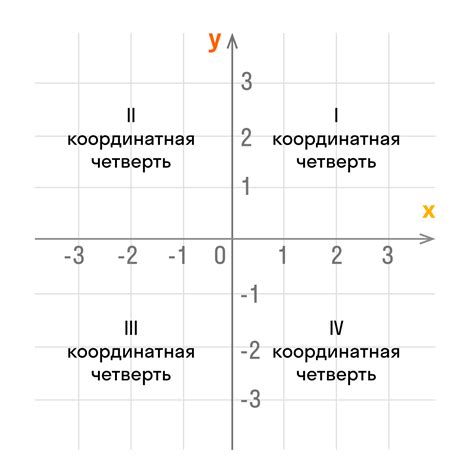
Для определения пересечений отрезков лучей в пространстве необходима система координат. Обычно используется декартова система координат, где каждая точка задается уникальными значениями координат X, Y и иногда Z. Для каждого отрезка или луча задаются начальная и конечная точки с соответствующими координатами. При пересечении лучей или отрезков необходимо проверить их координаты относительно друг друга, чтобы определить, действительно ли они пересекаются.
Параметры отрезков для анализа
Для определения возможности пересечения двух отрезков необходимо анализировать их параметры. Основные параметры отрезков включают:
1. Координаты конечных точек: Положение начальной и конечной точек определяет длину и ориентацию отрезка.
2. Угол наклона: Угол наклона отрезка относительно оси координат влияет на его направление и быстроту изменения координат.
3. Длина: Длина отрезка является важным параметром при анализе пересечения с другими отрезками.
При анализе пересечения двух отрезков необходимо учитывать и сравнивать данные параметры для определения возможности и условий пересечения.
Математический подход к задаче

Для того чтобы определить возможность пересечения двух отрезков луча, необходимо применить математические методы и правила геометрии. Сначала определяются координаты и уравнения отрезков и луча, затем проводится анализ их взаимного расположения. При этом учитывается условие, что для пересечения отрезков линии должны иметь общую точку на плоскости. Различные случаи соотношения отрезков могут быть рассмотрены с помощью геометрических методов и вычислений. Такой подход позволяет строго определить, может ли луч быть пересечением двух отрезков и каково их взаимное расположение.
Описание алгоритма проверки пересечения
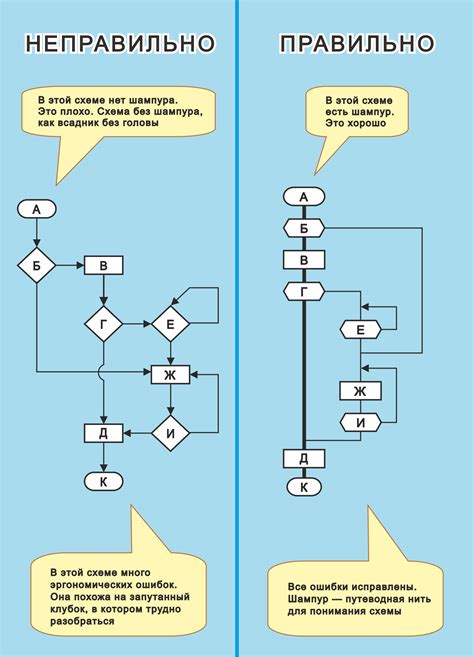
Для проверки пересечения двух отрезков необходимо следующие шаги:
| Шаг | Действие |
|---|---|
| 1 | Вычислить уравнения прямых, содержащих отрезки |
| 2 | Проверить, лежат ли концы одного отрезка по разные стороны относительно прямой, содержащей другой отрезок |
| 3 | Повторить предыдущий шаг, поменяв роли отрезков между собой |
| 4 | Проверить, лежат ли концы отрезков на разных сторонах относительно прямой, содержащей первый отрезок |
| 5 | Проверить, лежат ли концы отрезков на разных сторонах относительно прямой, содержащей второй отрезок |
| 6 | Если все условия выполнены, считать отрезки пересекающимися |
Примеры вычислений для наглядного понимания
Для наглядного понимания рассмотрим пример:
- Отрезок AC с координатами A(1, 3) и C(4, 6)
- Отрезок BD с координатами B(2, 5) и D(6, 1)
Теперь вычислим координаты точки пересечения луча AB и луча CD.
- Найдем уравнение прямой AB:
- k = (5 - 3) / (2 - 1) = 2
- Уравнение прямой: y = 2x + 1
- k = (1 - 6) / (6 - 4) = -5/2
- Уравнение прямой: y = -5/2x + 13
- 2x + 1 = -5/2x + 13
- x = 3
- y = 7
Таким образом, точка пересечения двух лучей будет P(3, 7).
Особенности расчета для вертикальных отрезков

Вертикальные отрезки имеют особенности при расчетах и пересечении с другими отрезками. В отличие от горизонтальных отрезков, вертикальные отрезки имеют бесконечные угловые коэффициенты, так как их наклон равен бесконечности. При определении пересечения вертикального отрезка с другим отрезком необходимо учитывать эту особенность.
Для вертикального отрезка необходимо определить его координаты x и y, а также длину отрезка. При определении пересечения с другим отрезком необходимо учитывать, что вертикальный отрезок будет проходить через точку пересечения со вторым отрезком с бесконечной наклонной линией.
Известные методы решения задачи в программировании

Существует несколько известных методов решения задачи по определению пересечения двух отрезков. Некоторые из них можно назвать классическими:
| 1. Метод пересечения отрезков |
| 2. Метод векторного произведения |
| 3. Метод уравнений прямых |
Каждый из этих методов имеет свои преимущества и недостатки, и выбор конкретного подхода зависит от поставленной задачи и требований к точности вычислений. Различные алгоритмы также могут быть использованы для определения пересечения отрезков в программировании, в зависимости от конкретной реализации и условий задачи.
Вопрос-ответ

Можно ли луч засечь, пересекая два отрезка?
Да, луч может быть пересечением двух отрезков. Если два отрезка имеют общую точку, то луч, исходящий из этой точки и направленный вдоль одного из отрезков, будет пересечением обоих отрезков.
Каким образом луч может быть образован пересечением двух отрезков?
Если два отрезка имеют общую точку и луч проходит через эту точку, направленный в одном из направлений, то этот луч будет являться пересечением обоих отрезков.
Является ли возможным теоретически создать луч, пересекающий два отрезка?
Да, теоретически возможно создать луч, который будет являться пересечением двух отрезков, если эти отрезки имеют общую точку и луч направлен вдоль одного из отрезков.
Какие условия должны быть выполнены, чтобы создать луч, пересекающий два отрезка?
Для того чтобы создать луч, который будет пересечением двух отрезков, необходимо, чтобы эти отрезки имели общую точку и луч проходил через эту точку, направленный в одном из направлений.
В каких случаях луч может быть иным от пересечения двух отрезков?
Луч может быть иным от пересечения двух отрезков только в том случае, если не выполнены условия пересечения: отрезки не имеют общей точки или луч не проходит через эту точку, направленный вдоль одного из отрезков.



