Геометрия – одна из древнейших наук, изучающая пространственные и пространственно-временные отношения. В рамках ее изучения возникают разнообразные вопросы, порой заслуживающие внимания и дополнительного обсуждения. Одним из таких вопросов является возможность прямой быть параллельной самой себе.
Слово «параллельно» связано с понятием равнозначности или однородности. Параллельные прямые никогда не пересекаются, они расположены на одинаковом расстоянии друг от друга в любой точке. Однако, казалось бы, возможно ли, чтобы прямая могла быть параллельна сама себе?
Геометрия прямых: основные понятия
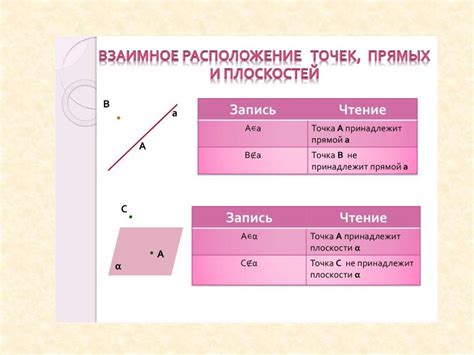
Параллельные прямые - это две прямые линии, которые расположены на одной плоскости и никогда не пересекаются.
Перпендикулярные прямые - это две прямые линии, которые пересекаются и образуют прямой угол, равный 90 градусам.
Угол наклона прямой - это угол, под которым прямая линия отклоняется от горизонтальной плоскости.
Прямая и ее свойства
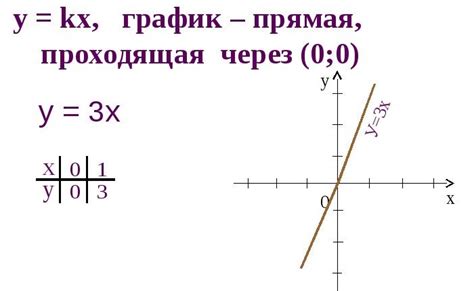
1. Прямая однозначно определяется двумя точками. Любые две точки на плоскости можно соединить прямой.
2. Прямая делит плоскость на две половины: сверху и снизу (или слева и справа). Точки, лежащие на одной стороне от прямой, не пересекаются с точками на другой стороне.
3. Прямая может быть параллельна другой прямой, если они не пересекаются и не сходятся нигде на плоскости. Параллельные прямые имеют одинаковый наклон или лежат на одинаковом расстоянии друг от друга.
Параллельные прямые: определение и признаки
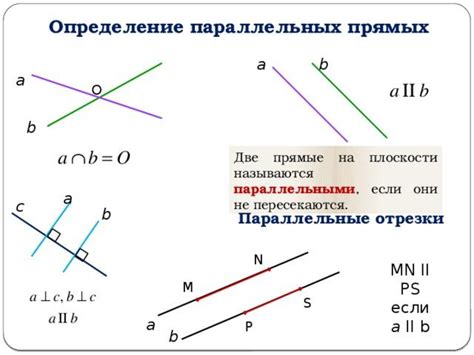
Для определения параллельных прямых можно использовать следующие признаки:
1. Прямые имеют одинаковый угловой коэффициент (наклон).
2. Углы, образуемые прямыми с пересекающей и под прямым углом, равны между собой.
3. Прямые параллельны плоскости, если углы, образуемые ими с наклонной прямой, равны.
Интересные факты о геометрии прямых

2. Две прямые могут быть параллельными, если они не пересекаются ни в одной точке. В геометрии это обозначается знаком



