В мире геометрии существует множество интересных и увлекательных вопросов, одним из которых является возможность провести прямую, которая будет пересекать две другие. Этот вопрос заставляет нас обратиться к основам геометрии и беседовать о свойствах линий, их взаимодействии и возможностях.
Когда говорим о прямых, мы вспоминаем, что они представляют собой геометрические объекты, не имеющие начала и конца. Они стремятся простирается в бесконечность и обладают бесконечным количеством точек. Линии являются важными инструментами в геометрии, и мы сталкиваемся с ними повсюду: от строительства до конструкции графиков.
Возможность провести прямую, пересекающую другие, зависит от последовательности или угла между ними. Когда говорим о пересечении двух прямых, мы подразумеваем точку, в которой они встречаются. Однако, мы также можем встретиться с ситуациями, когда линии никогда не пересекаются и протекают параллельно друг другу. Возникает вопрос: что делать, если мы хотим провести прямую, которая пересекала бы две другие?
Преимущества установления линии, касающейся двух других
В жизни часто возникают ситуации, когда необходимо произвести обозначение в пространстве, которое одновременно пересекало бы две уже существующие линии и служило бы для конкретизации их взаимного расположения. В таких случаях эффективным решением может оказаться проведение прямой, которая пересечет две другие и поможет успешно определить их взаимное положение.
Установление такой линии позволяет не только уточнить границы и направления существующих линий, но также предоставляет возможность определить точку пересечения и дать количественное выражение различным параметрам и характеристикам этого пересечения. В результате, проведение прямой, касающейся двух других, способствует более точному и детальному описанию пространства и объектов.
Кроме того, такая линия может также служить ориентиром при проведении дальнейших манипуляций или действий в данном пространстве. Она создает определенную ось или плоскость, которая может быть использована в качестве точки отсчета или ориентации при строительстве, измерениях или любых других процедурах, где требуется точное определение локации объектов.
Таким образом, необходимость установления прямой, пересекающей две другие, обусловлена возможностью более точно определить взаимное расположение и связь между существующими линиями, а также создать удобную базу для дальнейшего взаимодействия с объектами в данном пространстве.
Ограничения при попытке провести линию, пересекающую две другие
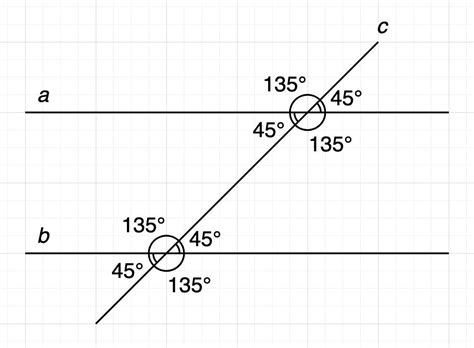
В определенных ситуациях возникают ограничения и сложности при попытке провести прямую линию, которая пересекает две уже существующие линии. Это может произойти из-за различных факторов и условий, которые могут быть связаны как с математическими, так и с физическими ограничениями. При проведении такой линии необходимо учитывать совместимость уже существующих линий, а также возможность их пересечения без нарушения основных правил и геометрических принципов.
Ограничение 1: При попытке провести линию, которая должна пересечь две другие линии, может возникнуть проблема с их взаимодействием. Например, если эти линии параллельны и находятся на одной плоскости, то провести линию, которая будет пересекать обе, не представляется возможным. В таких случаях требуется изменение положения или угловой ориентации хотя бы одной из линий, чтобы создать возможность для пересечения. |
Ограничение 2: Другим ограничением может быть свободное пространство, в котором происходит попытка провести линию пересечения. Если между уже существующими линиями недостаточно места или они находятся очень близко друг к другу, то провести новую линию может оказаться невозможным затруднительным. Возможно, потребуется перемещение или изменение формы одной или обеих линий, чтобы создать достаточное пространство для проведения линии пересечения. |
Ограничение 3: Физические ограничения также могут играть роль в попытке провести линию пересечения. Например, если уже существующие линии представляют собой стены или преграды, то провести линию, пересекающую их, может быть практически невозможно или требовать специальных инструментов и навыков. В таких случаях нужно принимать во внимание физическую природу и структуру уже существующих линий, чтобы определить возможность и метод пересечения. |
Сценарии взаимного перекрещивания двух прямых
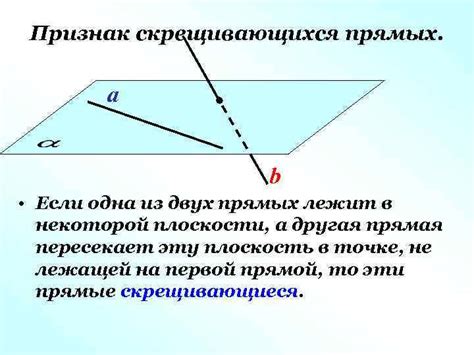
Разберем несколько возможных вариантов, в которых две прямые могут встретиться на перекрестке своих трасс.
Возможен сценарий, когда линии пресекаются в точке, образуя перпендикуляр. В данном случае одна прямая будет вертикальной, а вторая - горизонтальной. Пересечение происходит в точке, где они пересекаются под прямым углом. Это является одним из самых часто встречаемых и фундаментальных сценариев пересечения прямых.
В случае, когда две прямые пересекаются и образуют угол, не равный 90 градусам, возникает еще один вариант перекрестия. В этом случае, прямые сходятся в точке, образуя угол, неравный прямому углу. Такое пересечение может свидетельствовать о различных свойствах и взаимоотношениях прямых.
Это лишь некоторые из возможных сценариев пересечения прямых. Каждый отдельный случай требует отдельного рассмотрения и анализа, поскольку он может иметь уникальные особенности и последствия.
Применение пересечения прямых в практических задачах

Возможности пересечения прямых находят применение в различных областях человеческой деятельности. Пересечение прямых позволяет решать задачи, связанные с определением точек пересечения, нахождением углов и расстояний, а также построением графиков и моделей различных объектов.
| Область применения | Примеры задач |
|---|---|
| Геометрия | Определение пересечений прямых на плоскости, построение треугольников и угловых отношений, решение задач на конструкцию геометрических фигур. |
| Инженерия | Определение точек пересечения прямых линий, используемых при проектировании дорожных сетей, электрических цепей, трубопроводов и других инженерных систем. |
| Физика | Анализ движения тела по прямым траекториям, определение точек пересечения падающего тела с плоскостью и другими объектами, измерение углов и расстояний в физических экспериментах. |
| Финансы | Анализ графиков и экономических показателей, определение точек пересечения линий доли рынка, роста акций или процентных ставок. |
Это лишь некоторые примеры практического применения пересечения прямых. Знание основ геометрии и способов решения задач с использованием пересечений прямых может быть полезно и применимо во многих сферах нашей жизни.
Вопрос-ответ

Можно ли провести прямую, пересекающую две другие?
Да, можно провести прямую, которая пересекает две другие. Но это возможно только при определенных условиях. Зависит от расположения и взаимного положения заданных двух прямых.
Какие условия должны быть выполнены, чтобы провести прямую, пересекающую две другие?
Для проведения прямой, пересекающей две заданные прямые, условием является то, что эти две прямые должны быть некомпланарными. То есть они не должны находиться в одной плоскости.
Если две прямые лежат на одной плоскости, то можно ли провести прямую, пересекающую обе?
Нет, нельзя провести прямую, пересекающую две другие, если они находятся на одной плоскости. В этом случае, две прямые будут параллельными или совпадающими, и прямая, пересекающая обе, не сможет существовать.



