Четырехугольники и прямоугольники - это всем известные и широко используемые фигуры в геометрии. Они встречаются нам повсюду: в архитектуре, в дизайне, в нашей повседневной жизни. Но сколько на самом деле четырехугольников существует по сравнению с прямоугольниками?
Чтобы узнать ответ на этот вопрос, погрузимся в мир геометрии. Четырехугольник - это фигура, которая имеет четыре стороны. Он может быть выпуклым или невыпуклым, регулярным или нерегулярным. Прямоугольник - это частный случай четырехугольника, у которого все углы равны 90 градусов. Таким образом, прямоугольник является особой разновидностью четырехугольника.
Интересно, что количество четырехугольников намного больше, чем количество прямоугольников. Для вычисления количества четырехугольников существуют специальные формулы и алгоритмы. Это сложная задача, требующая глубоких знаний математики и комбинаторики. В результате исследований было установлено, что количество четырехугольников в разы превышает количество прямоугольников.
История и классификация четырехугольников
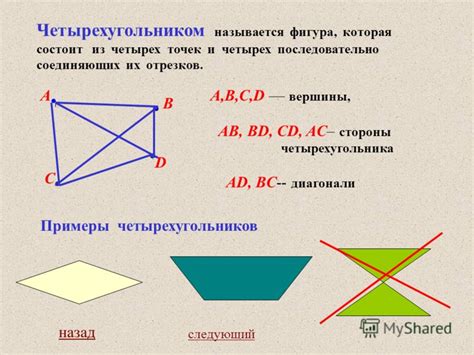
В истории геометрии четырехугольники изучались с древних времен. Уже в Египте и Месопотамии математики изучали прямоугольники и прямолинейные четырехугольники. В древней Греции Эвклид в своей работе "Начала" описал основные свойства четырехугольников и дал определения различных типов четырехугольников.
Существует несколько способов классификации четырехугольников. Один из них базируется на длине сторон и углов, а другой на параллельности и перпендикулярности сторон. В первом случае выделяют простые четырехугольники, такие как квадрат, ромб, прямоугольник и параллелограмм, а также сложные четырехугольники, такие как трапеция и трапецоид. Во втором случае выделяют параллелограммы, трапеции и трапецоиды.
Каждый тип четырехугольника имеет свои особенности и характеристики. Например, квадрат является частным случаем прямоугольника, у которого все стороны и углы равны. Ромб имеет все стороны равными, в то время как прямоугольник имеет противоположные стороны параллельными и перпендикулярными.
Знание о различных четырехугольниках имеет практическое применение в различных областях, включая архитектуру, графику и дизайн. Понимание и использование различных типов четырехугольников позволяет создавать более сложные и интересные фигуры и конструкции.
Виды и свойства четырехугольников
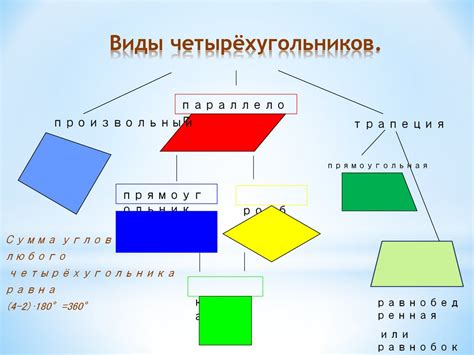
Основные виды и характеристики четырехугольников:
- Прямоугольник: четырехугольник, у которого все углы прямые (90 градусов).
- Квадрат: прямоугольник, у которого все стороны равны между собой.
- Параллелограмм: четырехугольник, у которого противоположные стороны параллельны друг другу.
- Ромб: параллелограмм, у которого все стороны равны между собой.
- Трапеция: четырехугольник, у которого две противоположные стороны параллельны, а остальные две - нет.
- Выпуклый четырехугольник: четырехугольник, у которого все внутренние углы меньше 180 градусов.
- Невыпуклый (вогнутый) четырехугольник: четырехугольник, у которого есть хотя бы один внутренний угол больше 180 градусов.
Каждый из этих видов четырехугольников имеет свои уникальные свойства и характеристики, которые делают их интересными объектами для изучения и анализа. Понимание этих свойств позволяет углубить знание о геометрии и ее применении в различных областях науки и техники.
Математические проблемы, связанные с четырехугольниками

Проблема о квадрате
Проблема о квадрате является одной из классических математических задач, связанных с четырехугольниками. Ее суть заключается в поиске четырехугольника, который можно разделить на равные части и перестроить в квадрат.
Эта проблема имеет древние корни и была известна уже в греческой математике. Она продолжает заинтриговывать ученых и математиков по сей день. Хотя некоторые примеры четырехугольников, которые можно разделить на равные части и перестроить в квадрат, были найдены, однако общее решение данной проблемы до сих пор не найдено. Это остается открытой математической задачей.
Трисектриса и четырехугольники
Еще одна интересная математическая проблема связана с трисектрисами и четырехугольниками. Трисектриса - это линия, которая делит угол на три равные части. Одной из важных задач, связанных с четырехугольниками, является поиск четырехугольника, у которого все четыре стороны являются отрезками трисектрисы данного угла.
Эта проблема вызывает большой интерес в математическом сообществе и до сих пор не имеет общего решения. Однако индивидуальные примеры четырехугольников, удовлетворяющих данному условию, были найдены при определенных значениях углов. Это подтверждает сложность задачи и позволяет предполагать, что общее решение может быть очень сложным или даже невозможным.
Проблема об углах и сторонах
Еще одна интересная проблема связана с углами и сторонами четырехугольников. В ней требуется найти условия, при которых сумма внутренних углов и сумма длин сторон четырехугольника будут равны между собой.
Хотя данная проблема может показаться несложной на первый взгляд, она имеет много вариаций и дополнительных условий. Например, существуют специальные классы четырехугольников, для которых данное условие выполняется. Однако для произвольных четырехугольников с общим решением данной проблемы все еще остается неразрешимой задачей.
Интересные факты о прямоугольниках

1. Прямоугольники вокруг нас
Прямоугольники можно увидеть практически везде: на домах, окнах, дверях, упаковках, сигнальных табличках и т.д. От простых бумажных прямоугольников до сложных структур – они составляют основу многих объектов в нашей повседневной жизни.
2. Свойства прямоугольников
Прямоугольник имеет несколько характеристик, которые его определяют: длины сторон, площадь и периметр. Все стороны прямоугольника параллельны друг другу, а все углы равны 90 градусам. Эти свойства позволяют использовать прямоугольники в различных областях, например, в строительстве и дизайне.
3. Математические приложения
Прямоугольники широко применяются в математике и физике. Они служат основой для изучения геометрии и алгебры, а также используются в задачах измерения и моделирования. Прямоугольные координаты широко используются в математических моделях и компьютерной графике.
4. Прямоугольники и искусство
Прямоугольники играют важную роль в искусстве и дизайне. Они используются для создания пропорций, композиции и рамок. Прямоугольники также могут быть основой для абстрактной геометрической живописи, где прямые линии и геометрические формы создают сложные композиции и впечатляющие эффекты.
5. Фрактальные прямоугольники
Фракталы – это геометрические фигуры, которые повторяются внутри самих себя. Прямоугольники могут быть основой для создания некоторых фракталов, например, в фрактальном искусстве или генерации текстур. Эти фракталы обладают сложной и красивой структурой, которая может быть исследована с помощью математики и компьютерных алгоритмов.
Применение прямоугольников в архитектуре и дизайне

В архитектуре прямоугольники используются для создания планов зданий и помещений. Они служат базисом для размещения комнат, залов, коридоров и других функциональных зон. Прямоугольные формы позволяют оптимально использовать пространство и обеспечивать удобство и эргономичность в планировании.
Прямоугольники также отлично вписываются в современные тренды в дизайне интерьера. Благодаря своей простоте и геометричности, они придают стильный и современный вид пространству. Прямоугольные формы широко применяются в мебели, отделке стен, полов и потолков, а также в создании различных декоративных элементов.
В дизайне ландшафта прямоугольники применяются для создания геометрических элементов и формирования пространств. Они могут быть использованы для создания прямых дорожек, террас, газонов или цветочных клумб. Прямоугольные формы помогают структурировать ландшафт и создавать симметрию и гармонию в окружающем пространстве.
В искусстве прямоугольники воплощаются в различных произведениях. Они могут быть использованы в картинах и графических работах для создания основного каркаса или композиционного центра. Прямоугольники также являются одними из основных элементов в изобразительном и архитектурном моделировании, позволяя создавать объемные и рельефные формы.
Таким образом, прямоугольники играют важную роль в архитектуре и дизайне, обеспечивая функциональность, эстетичность и гармонию в создании различных объектов и пространств.
Статистика использования прямоугольников в графическом дизайне

| 1. Форматы прямоугольников | 2. Применение прямоугольников | 3. Распространенные размеры |
|---|---|---|
| Прямоугольники могут быть разных форматов, таких как горизонтальные, вертикальные, квадратные и произвольные. | Они используются для создания рамок вокруг изображений, разделителей контента, кнопок, форм, баннеров и других визуальных элементов. | Распространенные размеры прямоугольников в дизайне - 300x250 пикселей (баннер), 728x90 пикселей (большой баннер), 800x600 пикселей (стандартный размер веб-страницы). |
| Горизонтальные прямоугольники шире, чем высокие. | Прямоугольники могут использоваться для создания отрицательного пространства и эффектов ломаной линии. | Другие популярные размеры прямоугольников: 336x280 пикселей, 300x600 пикселей, 160x600 пикселей. |
| Вертикальные прямоугольники выше, чем широкие. | Прямоугольники могут быть адаптированы для создания панелей навигации, заголовков, футеров и других элементов дизайна. | Веб-баннеры часто имеют соотношение сторон 3:1, например, 300x100 пикселей. |
| Квадратные прямоугольники имеют одинаковые стороны. | Прямоугольники могут использоваться для создания галерей, промо-блоков и других элементов с равными сторонами. | Интерактивные элементы в дизайне, такие как кнопки, часто имеют форму прямоугольников. |
| Произвольные прямоугольники имеют разные стороны и формы. | Использование прямоугольников с плавными закругленными углами может придать дизайну мягкость и современность. | Прямоугольники могут быть использованы для выделения важных элементов на веб-странице или в макете. |
Прямоугольники широко применяются в дизайне благодаря своей простоте и универсальности. Они являются основным строительным блоком для многих элементов и композиций, обеспечивая красоту и функциональность графического дизайна.
В данной статье мы рассмотрели интересные факты о том, сколько четырехугольников существует по сравнению с прямоугольниками. Мы выяснили, что количество четырехугольников значительно превышает количество прямоугольников.
Также мы обратили внимание, что каждый прямоугольник является четырехугольником, но не каждый четырехугольник является прямоугольником. Это связано с тем, что прямоугольник - это специфическая форма четырехугольника, имеющая четыре прямых угла.
Интересно отметить, что количество четырехугольников может быть бесконечным, так как существует множество способов соединения четырех точек. Однако, некоторые четырехугольники могут быть искаженными или неправильными, не обладать прямыми углами.
В целях более точного определения количества четырехугольников необходимо учитывать дополнительные условия, такие как: размер сторон, углы, параллельность сторон и другие свойства.
В зависимости от конкретных параметров, количество возможных четырехугольников может изменяться в широком диапазоне. Исследования этой темы помогут углубить понимание геометрии и ее приложений в различных областях науки и техники.