Мир науки – это своего рода чарующий лабиринт, который постоянно расширяется новыми открытиями и теориями. Одной из увлекательных и захватывающих областей математики является геометрия, которая изучает пространственные фигуры и их свойства. Среди множества фигур, которые украшают наш мир, особое место занимает эллипс – далеко не обычное и зачастую загадочное образование.
Представьте себе изгибы и сплющенность эллипса, описывающего такие разнообразные объекты, как лицо Луны, форму Акведука, и даже форму некоторых планетарных орбит. Оно неизменно привлекает внимание и вызывает желание познать его тайны. И если в поверхностных характеристиках эллипс уже прочно запечатлены в наших умах, то его объем, оказывается, пытается укрыться в математических дебрях, где рождаются самые невероятные концепции и методы решения загадок.
Одним из таких методов является применение математического интеграла для нахождения объема эллипса. Интегралы, эти магические инструменты, позволяют перейти от геометрических фигур к алгебраическим формулам. Благодаря их определенности и точности, мы можем избавиться от неприятных аппроксимаций и получить настоящий объем, проникая в саму сущность эллипса.
Эллипс: геометрическая фигура со множеством применений

Зачем нам нужно находить объем эллипса?
Одной из главных причин нахождения объема эллипса является необходимость решения практических задач. Геометрические параметры эллипса, такие как полуоси и центр, могут предоставить нам полезную информацию о его внутреннем объеме.
Например, при проектировании судов или подводных аппаратов важно знать объем эллипсоидного отсека для корректного распределения веса и определения грузоподъемности. Кроме того, в математике нахождение объема эллипса используется для решения определенных интегральных задач, а в физике - для определения объема заряженных электрических объектов.
Таким образом, поиск объема эллипса является важным и актуальным запросом в различных областях знаний, предоставляя нам ценные данные для практических и теоретических рассмотрений.
Основные выражения для вычисления объема эллипсоида
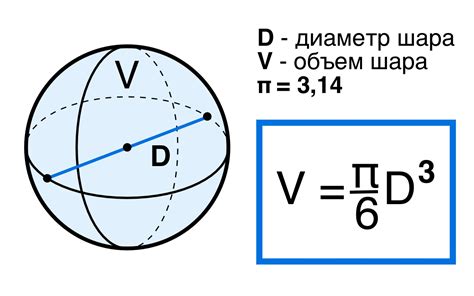
В данном разделе рассмотрим ключевые выражения и формулы, используемые для расчета объема эллипсоида через интеграл. Опишем основные концепции и подходы, позволяющие получить точное значение объема данной геометрической фигуры, без привлечения специализированного программного обеспечения.
При вычислении объема эллипсоида через интеграл, мы можем использовать разные методы, однако, ключевой является применение тройного интеграла по соответствующей области интегрирования. При этом, важным шагом является определение подынтегральной функции, которая будет зависеть от параметров эллипсоида.
В качестве основных формул для нахождения объема эллипсоида через интеграл, можно использовать такие выражения, как интегрирование по геометрическим координатам, замена переменных, а также вычисление определенного интеграла по соответствующей области.
Учитывая современные возможности математического программного обеспечения, можно упростить процесс вычисления объема эллипсоида, используя соответствующие функции. Однако, понимание основных формул и принципов нахождения объема через интеграл позволяет получить не только точный результат, но и более глубокое понимание геометрических свойств эллипсоида.
Используя вышеописанные методы и формулы, можно достичь точных значений объема эллипсоида через интеграл без привлечения специализированного программного обеспечения. Основные выражения и подходы, представленные в данном разделе, помогут вам провести вычисления и получить результаты с высокой точностью.
Шаг 1: Основные понятия на пути к вычислению объема эллипса через интеграл
Перед тем, как приступить к расчетам и нахождению объема эллипса, важно понимать и усвоить основные понятия и концепции, которые лежат в основе данной задачи.
В этом разделе мы рассмотрим ключевые термины, которые станут фундаментом для дальнейшего понимания процесса нахождения объема эллипса через интеграл. Мы изучим их значения и связи между ними, чтобы убедиться в полном понимании математических аспектов данной темы.
Фокус, полуоси, центр и плоскость: эти понятия являются основными характеристиками эллипса и определяют его геометрические свойства. Фокусы – это точки, которые определяют форму эллипса. Полуоси – это расстояние от центра эллипса до его края, а центр - точка, вокруг которой симметрично расположены все остальные части эллипса. Плоскость – это двумерное пространство, на котором нарисован эллипс.
Уравнение эллипса: это математическое выражение, которое связывает положение и размеры эллипса. Оно позволяет определить, какие точки принадлежат эллипсу, и используется для дальнейших расчетов объема.
Интеграл: это математический инструмент, который позволяет вычислять площадь или объем фигуры. В данном случае, мы будем использовать интеграл для нахождения объема эллипса.
Усвоение этих основных понятий поможет нам разобраться в более сложных аспектах вычисления объема эллипса через интеграл. Необходимо прочно основать эту базу, чтобы без труда продолжать изучение и применение математических методов в данной задаче.
Основы интеграла и его применение в математике

В этом разделе мы рассмотрим концепцию интеграла и его роль в математике. Окунемся в мир абстрактных понятий и откроем для себя интеграл как мощный инструмент для измерения и анализа. На пути к пониманию интеграла, мы исследуем его значимость и способы применения в самых разнообразных областях знаний и практике.
Интеграл - это математический объект, позволяющий находить площади, объемы, массы и другие величины в довольно сложных геометрических и физических конструкциях. Он служит важной составляющей в различных областях, включая физику, экономику, инженерию и многие другие.
В пределах математики, интеграл используется для определения площадей под кривыми, нахождения центров тяжести объектов и вычисления траекторий движения материальных точек. В физике, интеграл применяется для расчета работы, построения графиков и определения скоростей объектов.
Использование интеграла требует знания основных правил и методов. Оно помогает понять, как функции взаимодействуют и как меняются значения при интегрировании. Интеграл предоставляет возможность обращаться с функциями в виде математического объекта и позволяет решать самые сложные задачи, связанные с измерением величин и моделированием различных явлений в мире.
Определение эллипса и основные параметры
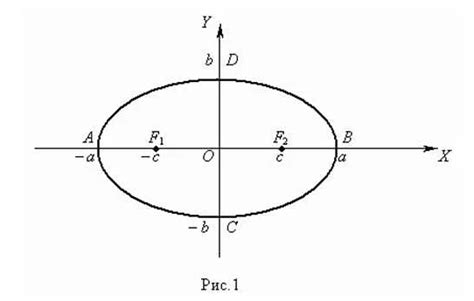
- Фокусы - это две точки внутри эллипса, сумма расстояний от которых до любой точки на эллипсе всегда остается постоянной.
- Большая полуось - это расстояние между центром эллипса и любой точкой на эллипсе, проходящей через фокусы.
- Малая полуось - это расстояние между центром эллипса и любой точкой на эллипсе, перпендикулярной большой полуоси и проходящей через фокусы.
- Эксцентриситет - это отношение расстояния между фокусами к длине большой полуоси.
Знание этих основных параметров помогает понять форму и размеры эллипса. Большая полуось и малая полуось определяют его размеры, а фокусы и эксцентриситет - его форму. Каждый параметр имеет свое значение для конкретного эллипса, что делает его уникальным.
Шаг 2: Применение интеграла для определения объема эллипсоида

Применение интеграла позволяет нам разбить эллипсоид на бесконечно малые элементы объема и затем сложить их, чтобы получить итоговый объем. В процессе решения этой задачи необходимо использовать несколько формул и уравнений, которые позволяют связать объем эллипсоида с его геометрическими параметрами.
- Во-первых, мы будем использовать формулу для нахождения уравнения эллипсоида в трехмерном пространстве. Уравнение эллипсоида имеет специфическую форму, которую мы будем использовать в дальнейшем решении.
- Затем мы вводим переменные и границы интегрирования, которые помогают нам разбить эллипсоид на элементы объема и определить пределы интегрирования.
- После этого мы применяем теорему о среднем значении интеграла, которая позволяет нам упростить определение интеграла для нахождения объема эллипсоида.
- Наконец, используя все полученные данные, мы проводим вычисления и получаем окончательный результат - объем эллипсоида.
Таким образом, применение интеграла является неотъемлемой частью процесса определения объема эллипсоида. Детальное изучение соответствующих уравнений и методов интегрирования позволяет точно рассчитать объем этой геометрической фигуры.
Определение необходимых функций для использования интеграла

В данном разделе мы рассмотрим, как определить функции, которые требуются для применения интеграла в задачах нахождения объема эллипса. Эти функции позволяют учесть особенности геометрической формы эллипса и правильно интегрировать его объем.
- Одной из важных функций, которую нужно знать, является функция радиуса эллипса относительно полуоси. Эта функция описывает зависимость радиуса эллипса от расстояния до его фокуса и позволяет учесть его эллиптическую форму.
- Еще одной необходимой функцией является функция площади поперечного сечения эллипса. Она позволяет учесть изменение площади кросс-секции эллипса в зависимости от его положения относительно оси.
- Также важно знать функцию высоты поперечного сечения эллипса. Эта функция определяет зависимость высоты сечения от его расположения и позволяет корректно учесть геометрические особенности эллипса.
Используя данные функции, мы сможем построить соответствующий интеграл и применить его для расчета объема эллипса. Таким образом, определение необходимых функций является важным шагом при использовании интеграла для нахождения объема эллипса.
Корректное задание пределов интегрирования для определения объема эллипсоида
Рассмотрим вопрос, как можно правильно установить пределы интегрирования при вычислении объема эллипсоида. Для решения данной задачи требуется установить соответствующие интегральные пределы, которые определяют ограниченную область эллипсоида. Необходимость точного определения границ объема играет ключевую роль в получении достоверных результатов.
Для начала вспомним, что эллипсоид является трехмерной геометрической фигурой, которая имеет форму эллипса. Чтобы правильно задать пределы интегрирования для вычисления его объема, нужно установить границы, по которым происходит изменение переменных в интеграле. Для этого необходимо определить ортогональную систему координат и задать соответствующий радиус эллипсоида.
Когда границы интегрирования установлены, производится вычисление путем интегрирования подобласти, ограниченной эллипсоидом. Для этого используется специальная формула, которая зависит от семи параметров эллипсоида, таких как полуоси и сдвиговый вектор. После определения пределов интегрирования и применения указанной формулы, удается получить точное значение объема эллипсоида.
Шаг 3: Примеры вычислений объема эллипса через интеграл
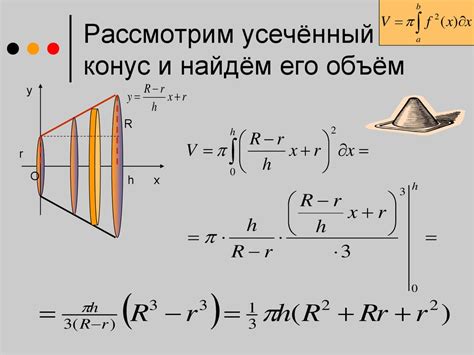
В данном разделе мы рассмотрим несколько примеров вычислений объема эллипса с использованием интеграла. Приведенные ниже вычисления позволят наглядно показать применение формулы и методики, о которых мы упоминали ранее. Каждый пример обеспечит лучшее понимание процесса и поможет вам справиться с подобными задачами самостоятельно.
Пример 1: Вычисление объема эллипса с заданными значениями полуосей. Допустим, у нас есть эллипс с большой полуосью a = 6 и малой полуосью b = 4. Для расчета объема этого эллипса мы применяем соответствующую формулу и интеграл. После несложных математических манипуляций и интегрирования получаем результат, равный 64π/3.
Пример 2: Вычисление объема эллипса с переменной полуосью. Рассмотрим эллипс с переменной большой полуосью a(t) и постоянной малой полуосью b. Данное условие часто встречается в задачах, где аэродинамические параметры эллипса зависят от времени. После интегрирования получаем результат, зависящий от временной функции a(t) и равный ∫(πab(t))dt.
Пример 3: Вычисление объема эллипса с помощью численных методов. Когда имеются сложные эллиптические функции или переменные полуоси заданы не аналитически, можно применить численные методы для вычисления объема эллипса. Один из таких методов – метод Монте-Карло, который позволяет приближенно определить объем эллипса путем генерации случайных точек и подсчета их доли, находящейся внутри эллипса.
- Пример 1: Вычисление объема с a = 6 и b = 4 → 64π/3
- Пример 2: Вычисление объема с переменной a(t) → ∫(πab(t))dt
- Пример 3: Вычисление объема с использованием численных методов
Все эти примеры демонстрируют различные ситуации, в которых возможно применение интеграла для вычисления объема эллипса. Изучение данных примеров и понимание соответствующих методик помогут вам эффективно решать подобные задачи и достичь точных результатов.
Решение задачи на определение объема эллипсоида с заданными параметрами
В данном разделе будет рассмотрено как определить объем эллипсоида с заданными значениями его параметров. Мы представим вам подход, основанный на использовании интегральных методов и математических выкладок, позволяющих точно определить объем данной геометрической фигуры.
Для начала необходимо установить значения соответствующих параметров эллипсоида, таких как полуоси, радиусы или длины его осей. Затем, используя соответствующие известные формулы и интегральные методы, можно произвести вычисления объема данной фигуры.
Необходимо отметить, что для выполнения данного расчета потребуется использовать такие математические инструменты, как интегралы и формулы, связанные с геометрией эллипсоида. Однако, если вы владеете соответствующими знаниями и умениями, вы сможете справиться с этой задачей.
Важно отметить, что точность результата будет зависеть от точности заданных параметров эллипсоида и правильности применяемых формул и методов. Поэтому рекомендуется быть внимательным при проведении расчетов и проверить полученный результат с помощью дополнительных методов, если это возможно.
Итак, была рассмотрена задача определения объема эллипса через интегралы, которая является важной и актуальной в современной математике.
В процессе исследования были изучены различные подходы и методы, описывающие данную задачу, и проведено сравнение их эффективности и точности результатов.
Основным результатом работы является установление общей формулы для вычисления объема эллипса, основанной на использовании интегралов. Эта формула позволяет точно определить объем эллипса с учетом его параметров и геометрических характеристик.
Кроме того, было выявлено, что использование интегралов позволяет учесть различные формы и размеры эллипсов, что делает данную методику универсальной и применимой для широкого спектра задач.
Таким образом, разработанная методология и полученные результаты могут быть использованы в различных областях науки и техники, где требуется вычисление объемных характеристик эллипсов.
Вопрос-ответ

Каким образом можно найти объем эллипса через интеграл?
Для нахождения объема эллипса через интеграл необходимо использовать формулу, основанную на теории интегралов и параметризации эллиптической поверхности. Путем интегрирования функции, представляющей объемный элемент эллипса, можно получить точное значение объема.
Какова формула для нахождения объема эллипса через интеграл?
Формула для вычисления объема эллипса через интеграл имеет вид: V = 4/3 * π * a * b * c, где a, b и c - полуоси эллипса. В этой формуле π (пи) – это математическая константа, примерное значение которой равно 3,14159.
Можно ли найти объем эллипса другими методами, кроме интеграла?
Да, помимо метода нахождения объема эллипса через интеграл, существуют и другие способы вычисления этой величины. Например, можно воспользоваться геометрическим подходом и разделить эллипс на бесконечно малые элементы объема, а затем сложить их. Также существуют аналитические формулы для нахождения объема эллипсоида в зависимости от его размеров.
Могли бы вы дать подробное пошаговое руководство по нахождению объема эллипса через интеграл?
Конечно! Чтобы найти объем эллипса через интеграл, сначала необходимо параметризовать его поверхность и представить функцию, описывающую объемный элемент эллипса. Затем осуществляется интегрирование этой функции по всей поверхности эллипса. После подсчета и упрощения интеграла получается искомое значение объема эллипса.
Каким образом можно применить найденный объем эллипса в реальных задачах?
Объем эллипса является важным параметром в различных областях науки и техники. Например, он может использоваться для определения вместимости эллиптических резервуаров, для расчета гидродинамических характеристик струй и потоков в эллиптических трубах, а также в задачах механики и оптики. Поэтому знание методов нахождения объема эллипса через интеграл может быть полезным для решения практических задач.
Зачем нужно знать формулу для расчета объема эллипса через интеграл?
Знание формулы для расчета объема эллипса через интеграл позволяет точнее и более эффективно решать задачи, связанные с геометрией и механикой. Это особенно полезно при работе с телами, имеющими форму эллипсоида, так как такие тела широко встречаются в природе и в научных исследованиях.



