Вписанная окружность в прямоугольном треугольнике касается всех трех сторон треугольника и описывается как окружность, которая вписана внутрь фигуры. Один из важных параметров вписанной окружности - это радиус, который можно найти с помощью простых математических формул и теорем.
Для нахождения радиуса вписанной окружности в прямоугольный треугольник можно воспользоваться формулой, которая зависит от длин сторон треугольника. Существует несколько способов решения данной задачи, включая использование формулы радиуса вписанной окружности и равенства площадей треугольника и круга.
В данной статье мы рассмотрим подробные шаги по нахождению радиуса вписанной окружности в прямоугольном треугольнике. Полученные знания помогут вам лучше понять геометрию и научиться решать подобные задачи.
Формула для нахождения радиуса вписанной окружности в треугольник
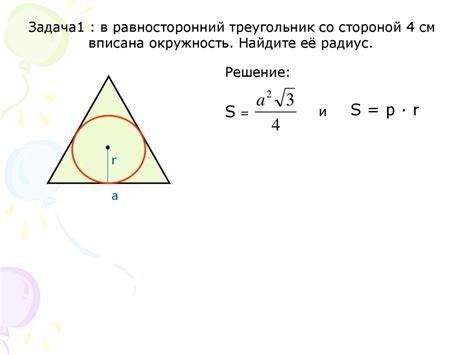
Для прямоугольного треугольника с катетами a и b и гипотенузой c радиус вписанной окружности можно найти по следующей формуле:
| Радиус вписанной окружности | : | r = (a + b - c) / 2 |
Прямоугольный треугольник и радиус окружности

Геометрические свойства вписанной окружности
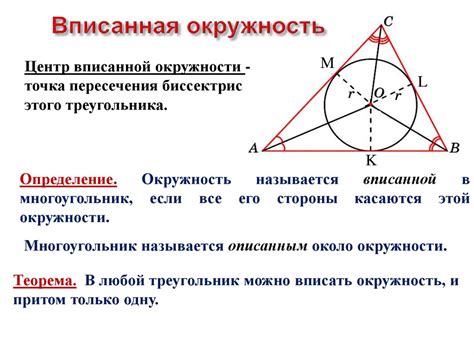
Точка пересечения сторон треугольника и окружности называется точкой касания. Соединив центр окружности с точками касания, получим радиус вписанной окружности.
Радиус вписанной окружности в прямоугольный треугольник задается формулой r = (a + b - c) / 2, где a и b - катеты, c - гипотенуза треугольника.
Как найти радиус вписанной окружности по сторонам треугольника
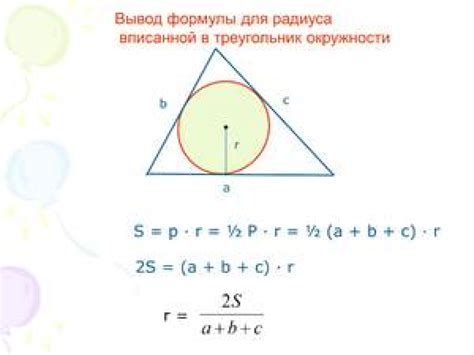
Для того чтобы найти радиус вписанной окружности в прямоугольный треугольник по известным сторонам, следует использовать формулу:
| R = P/2 - c |
Где R - радиус вписанной окружности, P - периметр треугольника, c - гипотенуза прямоугольного треугольника.
Для нахождения радиуса вписанной окружности необходимо знать периметр треугольника и длину гипотенузы. После подставления значений в формулу можно легко определить радиус вписанной окружности.
Пример решения задачи нахождения радиуса вписанной окружности
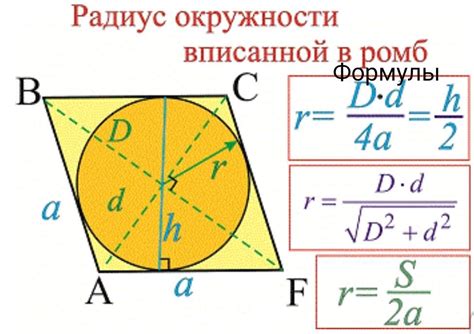
Для нахождения радиуса вписанной окружности в прямоугольный треугольник можно воспользоваться следующим методом:
- Найдем площадь треугольника по формуле: $S = \frac{a \cdot b}{2}$, где а и b - катеты треугольника.
- Найдем полупериметр треугольника: $p = \frac{a + b + c}{2}$, где a и b - катеты, c - гипотенуза.
- Найдем радиус вписанной окружности: $r = \frac{S}{p}$.
Таким образом, найдя площадь треугольника, полупериметр и радиус вписанной окружности, мы можем определить радиус вписанной окружности прямоугольного треугольника.
Практическое применение нахождения радиуса вписанной окружности
Знание радиуса вписанной окружности в прямоугольном треугольнике может быть полезным при решении различных задач и проблем. Например, зная радиус вписанной окружности, можно определить центральный угол, под которым стороны треугольника касаются этой окружности. Также радиус вписанной окружности позволяет вычислить площадь треугольника, зная длины его сторон. Кроме того, радиус вписанной окружности помогает понять свойства треугольника и его взаимное расположение относительно окружностей и других фигур.
Вопрос-ответ

Как найти радиус вписанной окружности в прямоугольный треугольник?
Для того чтобы найти радиус вписанной окружности в прямоугольный треугольник, нужно знать длины всех трех сторон треугольника. Далее необходимо использовать формулу: радиус = (периметр треугольника - сумма длин сторон) / 2. Здесь периметр треугольника равен сумме длин всех его сторон. Эту формулу можно применять в случае, когда известны все три стороны прямоугольного треугольника.
Какую формулу использовать для расчета радиуса вписанной окружности в прямоугольный треугольник?
Формула для расчета радиуса вписанной окружности в прямоугольный треугольник: радиус = (периметр треугольника - сумма длин сторон) / 2. Здесь периметр треугольника равен сумме длин всех его сторон. Эта формула основана на свойствах вписанной окружности, которая касается сторон треугольника и имеет центр в точке пересечения биссектрис треугольника.
Что нужно знать для нахождения радиуса вписанной окружности в прямоугольный треугольник?
Для нахождения радиуса вписанной окружности в прямоугольный треугольник нужно знать длины всех трех сторон треугольника. Далее используется формула: радиус = (периметр треугольника - сумма длин сторон) / 2, где периметр треугольника равен сумме длин всех его сторон. Также полезно знать, что вписанная окружность касается сторон треугольника и имеет центр в точке пересечения биссектрис треугольника.
Как узнать радиус вписанной окружности, если известны длины сторон прямоугольного треугольника?
Для того чтобы узнать радиус вписанной окружности, если известны длины сторон прямоугольного треугольника, нужно использовать формулу: радиус = (периметр треугольника - сумма длин сторон) / 2. Периметр треугольника равен сумме длин всех его сторон. Эта формула позволяет нам рассчитать радиус вписанной окружности, которая касается сторон треугольника и имеет центр в точке пересечения биссектрис треугольника.



