Часто мы сталкиваемся с задачами, в которых необходимо найти экстремумы функций. Однако, просто находить точки экстремума не всегда достаточно. Обычно мы также хотим знать, характеристику найденных точек: являются ли они максимумами или минимумами функции? Чтобы получить более полное представление о поведении функции вблизи критических точек, удобно использовать вторую производную функции.
Вторая производная функции - это производная от производной. Она позволяет нам получить информацию о изменении скорости приращения функции вблизи критической точки. Используя вторую производную, мы можем определить, как функция меняет свою выпуклость или вогнутость вблизи критической точки.
Как же это работает? Если вторая производная положительна в точке, то функция в этой точке будет выпуклой вниз, а значит, точка является локальным минимумом. Если же вторая производная отрицательна, то функция будет вогнутой в этой точке, и это будет означать, что точка является локальным максимумом. Если же вторая производная равна нулю, то у нас нет информации о характере критической точки, и необходимо проводить дополнительные исследования.
Зачем нужно определять экстремум и как это помогает в анализе функций?

В мире математики функции играют важную роль в описании различных явлений и моделировании разнообразных процессов. Концепция экстремума помогает понять и определить особые точки на графике функции, где функция достигает наибольших или наименьших значений. Знание вида экстремума позволяет нам более глубоко изучить свойства функции и предсказывать ее поведение в окрестности точки экстремума.
Понимание вида экстремума помогает нам определить, является ли точка максимумом или минимумом. Это важно для оптимизации, где поиск максимального или минимального значения функции является ключевым. Например, в экономике можно использовать понятие экстремума для определения оптимального уровня производства или ценовой стратегии. В физике, экстремумы могут указывать на равновесные состояния системы или максимальную энергию.
Если мы знаем, что функция имеет экстремум, то анализ формы экстремума может помочь нам понять и классифицировать функцию. Какие значения принимает функция вблизи точки экстремума? Является ли экстремум локальным или глобальным? Как свойства функции меняются при переходе через экстремальную точку? Ответы на эти вопросы дают нам лучшее понимание функции и ее поведения в окрестности экстремума.
Определение вида экстремума также позволяет нам решать определенные задачи и проблемы. Например, при оптимизации функций мы ищем точку экстремума, где производная равна нулю, чтобы найти максимальное или минимальное значение функции. Знание вида экстремума помогает нам правильно интерпретировать эту найденную точку и принимать соответствующие решения.
Основные понятия и цели анализа экстремума
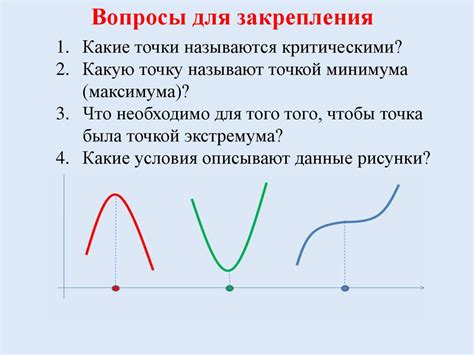
Основной целью анализа экстремума является определение точек, в которых функция достигает своих крайних значений. При этом, мы можем выделить два типа экстремумов - локальные экстремумы и глобальные экстремумы. Локальный экстремум это точка, в которой функция достигает максимального или минимального значения в своей окрестности, но может иметь значения вне этой окрестности, которые больше или меньше. Глобальный экстремум это точка, в которой функция достигает максимального или минимального значения на всем своем определенном интервале.
Для анализа экстремума функции используется теорема Ферма, которая утверждает, что если функция имеет экстремум в точке, то ее производная в этой точке равна нулю. Это является необходимым, но не достаточным условием для экстремума. Поэтому, помимо проверки равенства производной нулю, необходимо использовать вторую производную функции.
- Понятие локального и глобального экстремума функции;
- Условия Ферма для определения экстремума;
- Вторая производная и ее роль при анализе экстремума;
- Примеры решения задач на анализ экстремума.
Методы определения экстремума в функции

Раздел посвящен различным методам нахождения экстремума в функции, основываясь на второй производной. Здесь будут рассмотрены приемы, позволяющие определить тип экстремума, приближенные значения точек экстремума и их значения.
Перед тем как перейти к конкретным методам, важно понять, что экстремумы функции являются особенными точками, в которых функция достигает наибольшего или наименьшего значения. Определение типа экстремума может быть осуществлено с использованием второй производной функции, которая указывает на выпуклость или вогнутость графика.
В данном разделе рассмотрены следующие методы определения экстремума:
| Метод | Краткое описание |
|---|---|
| Исследование знаков второй производной | Определение типа экстремума на основе знаковой таблицы второй производной функции |
| Проверка изменения знака первой производной | Анализ возрастания и убывания функции перед и после точек экстремума |
| Использование окрестности точки экстремума | Приближенное нахождение точек экстремума путем анализа поведения функции в небольшой окрестности |
Каждый метод имеет свои преимущества и подходит для определенного типа функций. Понимание и применение этих методов позволит более точно определить экстремумы функции, что имеет важное значение в различных областях науки и инженерии.
Использование первой производной для определения точек экстремума

Когда мы говорим о первой производной функции, мы рассматриваем ее скорость изменения. Если значение первой производной положительно, то функция возрастает, а если отрицательно, то функция убывает. Точки, где значение первой производной меняется с положительного на отрицательное или наоборот, могут быть точками экстремума. Такие точки называются стационарными точками.
Чтобы определить, является ли стационарная точка экстремумом, мы обращаемся к знаку второй производной функции. Если вторая производная положительна в стационарной точке, то это указывает на локальный минимум, а если она отрицательна, то на локальный максимум. Если же вторая производная равна нулю или не существует, то этот метод не дает определенного ответа и необходимо использовать другие подходы для определения типа экстремума.
Важно отметить, что применение первой производной позволяет нам только выявить стационарные точки, которые могут быть экстремумами. Для более точного определения их типа, требуется дополнительный анализ с использованием второй производной и других методов.
Роль второй производной в анализе экстремума
Одной из основных задач математического анализа является определение и классификация экстремальных точек функции. Экстремумы могут быть максимумами (точками локального или глобального максимума) или минимумами (точками локального или глобального минимума). В общем случае, для определения вида экстремума нам требуется применять не только первую производную, но и вторую производную.
- Положительная вторая производная указывает на существование локального минимума в точке. Если вторая производная положительна, то это означает, что функция, приближаясь к данной точке слева и справа, имеет скорость роста, скорость которой уменьшается, что указывает на наличие ямы или впадины.
- Отрицательная вторая производная свидетельствует о существовании локального максимума в точке. Если вторая производная отрицательна, это означает, что функция, приближаясь к данной точке слева и справа, имеет скорость убывания, скорость которой увеличивается, что указывает на наличие горы или холма.
- Ноль второй производной может означать наличие перегиба в точке или отсутствие экстремума. В таком случае, для дальнейшего анализа могут потребоваться другие инструменты математического анализа.
Таким образом, вторая производная является важным компонентом в анализе экстремумов и позволяет нам определить их вид – минимумы или максимумы. Зная значение второй производной, мы можем более точно определить поведение функции вокруг точки экстремума и провести более глубокий анализ функциональных зависимостей.
Критерии установления характера экстремума с помощью второй производной
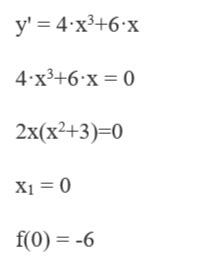
Выпуклость и вогнутость функции обусловлены знаком второй производной - она может быть положительной или отрицательной на данном интервале. Если вторая производная положительна на интервале, то функция является выпуклой, и точка экстремума будет являться точкой минимума. В случае, когда вторая производная отрицательна на интервале, функция будет вогнутой, и точка экстремума окажется точкой максимума.
Однако, если вторая производная равна нулю на интервале, то информацию о характере экстремума получить невозможно. Для полноты картины необходимо дополнительно использовать анализ первой производной и исследование поведения функции на границах интервала.
Таким образом, определение вида экстремума через вторую производную является важным инструментом анализа графиков и функциональных зависимостей. Учитывая значения второй производной на интервале и исследуя выпуклость или вогнутость функции, можно однозначно определить, является ли точка экстремума точкой максимума или минимума.
Применение методов анализа второй производной: наглядные примеры

Пример 1: Исследование функции на выпуклость
Рассмотрим функцию f(x), заданную на интервале (a, b), и предположим, что она имеет непрерывные вторые производные на этом интервале. Используя методы анализа второй производной, мы можем исследовать эту функцию на выпуклость. Если вторая производная положительна на всем интервале (a, b), то функция является выпуклой в этом интервале. Если вторая производная отрицательна на всем интервале (a, b), то функция является вогнутой в этом интервале. Если вторая производная меняет знак на интервале (a, b), то функция имеет точки перегиба.
Пример 2: Определение экстремума функции
Рассмотрим функцию g(x), заданную на отрезке [c, d], и предположим, что она имеет непрерывные вторые производные на этом отрезке. С помощью второй производной мы можем определить, являются ли точки x=c и x=d максимальным и минимальным значениями функции соответственно. Если вторая производная в точке x=c положительна, то функция имеет локальный минимум в этой точке. Если вторая производная в точке x=c отрицательна, то функция имеет локальный максимум в этой точке. Аналогично, если вторая производная в точке x=d положительна, то функция имеет локальный максимум в этой точке, и если вторая производная в точке x=d отрицательна, то функция имеет локальный минимум в этой точке.
Пример 3: Проверка условий допустимости экстремумов
Предположим, что функция h(x) обладает седловой точкой экстремума. Используя вторую производную, мы можем проверить условия допустимости этой точки. Если вторая производная в точке экстремума равна нулю и меняет знак с одной стороны на другую, то этот экстремум является седлом. Если же вторая производная в точке экстремума не меняет знак, то данная точка не является экстремумом.
Таким образом, методы анализа второй производной предоставляют нам ценные инструменты для понимания поведения функций вблизи экстремальных точек и определения их характера.
Вопрос-ответ

Как определить вид экстремума через вторую производную?
Чтобы определить вид экстремума через вторую производную, необходимо проанализировать знак второй производной функции в точке экстремума. Если вторая производная больше нуля, то это будет точка минимума, а если вторая производная меньше нуля - точка максимума.
Как связаны первая и вторая производные функции?
Первая производная функции отвечает за скорость изменения функции, а вторая производная - за ее ускорение. Если первая производная положительна и увеличивается, а вторая производная положительна, то функция имеет точку минимума. Если первая производная отрицательна и убывает, а вторая производная отрицательна, то функция имеет точку максимума.
В чем заключается геометрическая интерпретация второй производной функции?
Геометрическая интерпретация второй производной функции заключается в определении типа кривизны графика функции в конкретной точке. Если вторая производная положительна, то график выпуклый вверх и имеет точку минимума. Если вторая производная отрицательна, то график выпуклый вниз и имеет точку максимума.
Что происходит, если вторая производная равна нулю?
Если вторая производная функции равна нулю, то нельзя однозначно определить вид экстремума в данной точке. Для более точного анализа можно использовать третью производную или ряд Тейлора. В этом случае график функции может иметь точку перегиба.
Какие ошибки могут возникнуть при определении вида экстремума через вторую производную?
При определении вида экстремума через вторую производную возможны ошибки из-за некорректного определения точки экстремума или неправильного подсчета второй производной. Также нельзя забывать, что вторая производная может быть равна нулю в точке перегиба графика функции, что может привести к неправильной интерпретации.
Каким образом можно определить вид экстремума через вторую производную?
Для определения вида экстремума через вторую производную необходимо проанализировать знак этой производной в окрестности точки, в которой ищется экстремум. Если вторая производная положительна, то это указывает на наличие локального минимума. Если же вторая производная отрицательна, то это указывает на наличие локального максимума.



