Пересечение прямых в геометрии - одно из ключевых понятий, которое позволяет определить, пересекаются ли две прямые или нет. Для этого нужно рассмотреть уравнения прямых и провести несложные алгебраические операции.
Для начала стоит определить уравнения данных прямых. Представим их в виде y = k1*x + b1 и y = k2*x + b2, где k1, k2 - коэффициенты наклона, а b1, b2 - коэффициенты смещения по оси y.
Для того чтобы узнать, пересекаются ли прямые а и б, необходимо решить систему уравнений, полученных из вышеуказанных уравнений прямых. Если система имеет одно решение, прямые пересекаются в этой точке.
Методы проверки пересечения прямых

Существует несколько способов определения пересечения прямых аб и б:
- Графический метод: построить прямые на координатной плоскости и проверить, пересекаются ли они;
- Аналитический метод: решить систему уравнений, задающих прямые, и проверить существование и единственность решения;
- Геометрический метод: использовать свойства углов и расстояний между прямыми для определения их взаимного расположения;
- Векторный метод: представить прямые в виде векторных уравнений и проверить их взаимное положение.
Анализ коэффициентов уравнений

Для определения пересечения прямых аb и b необходимо проанализировать коэффициенты уравнений этих прямых. Если коэффициенты при x и y в уравнениях прямых равны, то прямые параллельны и не пересекаются. Если же коэффициенты при x и y в уравнениях различны, то прямые пересекаются и имеют общую точку пересечения.
| Прямая | Уравнение | Уравнение в общем виде |
|---|---|---|
| а | y = k₁x + b₁ | k₁x - y + b₁ = 0 |
| b | y = k₂x + b₂ | k₂x - y + b₂ = 0 |
Сравнивая коэффициенты k₁ и k₂ в уравнениях прямых, можно определить их взаимное положение относительно друг друга.
Построение графиков прямых
Для построения графика прямой на координатной плоскости необходимо провести две точки на прямой и соединить их прямой линией. Для этого можно выбрать две произвольные точки, подставить их координаты в уравнение прямой и найти координаты прямой на оси x. Затем проводим прямую по найденным точкам.
Таким образом, построив график прямой, можно визуально определить, пересекаются ли прямые аb и б.
Использование угловых коэффициентов

Для определения пересечения прямых аб и б нужно использовать угловые коэффициенты.
Угловой коэффициент прямой а равен tg(α) = (y2 - y1) / (x2 - x1), где (x1, y1) и (x2, y2) - координаты точек на прямой а.
Угловой коэффициент прямой б равен tg(β) = (y4 - y3) / (x4 - x3), где (x3, y3) и (x4, y4) - координаты точек на прямой б.
Если угловые коэффициенты прямых а и б равны, то они параллельны и не пересекаются. В противном случае, прямые пересекаются в точке (x, y), где x и y можно найти, решив систему уравнений прямых.
Применение метода определителя

- Шаги для определения пересечения прямых:
- Записать уравнения прямых в общем виде;
- Сформировать матрицу коэффициентов и матрицу свободных членов;
- Вычислить определители матриц;
- Провести анализ результата: если определитель не равен нулю, то прямые пересекаются в одной точке.
Изучение характеристик системы уравнений

Рассмотрение параллельных прямых
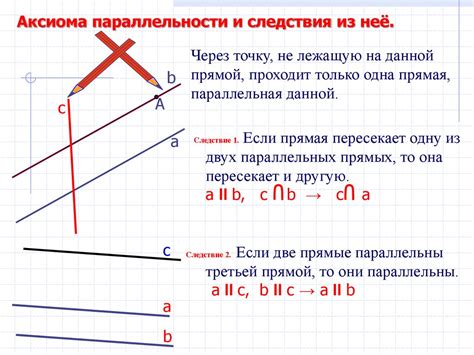
Две прямые называются параллельными, если они не пересекаются и все их точки расположены на одинаковом расстоянии друг от друга. Это означает, что угол между параллельными прямыми равен нулю или 180 градусов.
Для проверки параллельности прямых можно использовать различные методы, например, исследовать их угловые коэффициенты. Если угловые коэффициенты двух прямых равны, то они параллельны. Также можно провести прямые на координатной плоскости и проверить их взаимное расположение.
Примеры задач на пересечение

Рассмотрим несколько примеров задач, чтобы определить, пересекаются ли прямые ab и b:
| Пример 1: | Даны уравнения прямых: ab: y = 2x + 5 и b: y = -3x + 3. Найдем их точку пересечения. |
| Пример 2: | Уравнения прямых ab: x + y = 7 и b: x - y = 1. Определить, пересекаются ли данные прямые. |
| Пример 3: | Прямые ab и b заданы уравнениями: ab: 3x - 2y = 4 и b: 6x - 4y = 8. Найдем их точку пересечения, если она существует. |
Вопрос-ответ

Как определить пересекаются ли прямые аб и б?
Для определения пересечения прямых аб и б можно использовать метод подстановки. Для этого необходимо найти точку пересечения этих прямых, а затем подставить координаты этой точки в уравнения прямых. Если обе прямые удовлетворяются этими координатами, то они пересекаются, иначе нет.
Какие условия должны быть выполнены, чтобы прямые аб и б пересекались?
Для того чтобы прямые аб и б пересекались, необходимо, чтобы их уравнения были линейно независимыми, то есть прямые не должны быть параллельными. Также необходимо, чтобы обе прямые лежали в одной плоскости.
Можно ли определить пересечение прямых аб и б графически?
Да, пересечение прямых аб и б можно определить графически. Для этого необходимо построить графики уравнений этих прямых на координатной плоскости и проверить, имеют ли они общую точку пересечения. Если прямые пересекаются, то они будут иметь одну общую точку.
Что значит, что прямые аб и б параллельны?
Прямые аб и б называются параллельными, если они не имеют общих точек и направляющие векторы этих прямых коллинеарны. Это означает, что прямые расположены на одинаковом расстоянии друг от друга и никогда не пересекаются.
Что делать, если прямые аб и б не пересекаются?
Если прямые аб и б не пересекаются, то это означает, что они либо параллельны, либо лежат в разных плоскостях. В таком случае нужно проверить их уравнения и направляющие векторы. Если прямые параллельны, то можно определить расстояние между ними. Если прямые лежат в разных плоскостях, то они точно не пересекаются.



