Не замечали ли вы, что наше сознание так тесно связано с числами? Они окружают нас повсюду: в повседневных задачах, приближенных к реальности, а также в мистических и математических формулах, уводящих мысли в невероятные глубины. Но именно числа, вопреки своей видимой простоте, несут в себе потрясающую сложность и необычайные возможности.
Одним из самых захватывающих и важных аспектов числовой магии является позиционная система счисления. Ведь именно она позволяет нам представлять любые числа с помощью ограниченного набора символов и освобождает наш ум от необходимости запоминать длинные последовательности цифр.
Позиционная система счисления основана на принципе разделения чисел на разряды и установления их значения в зависимости от их позиции. Из этого простого принципа вытекает множество преимуществ, делающих позиционную систему незаменимой и необыкновенно эффективной в наших расчетах и вычислениях.
Идея позиционной системы счисления

Ключевым принципом работы позиционной системы счисления является учет степеней основания системы при записи числа. Каждая цифра, находящаяся в числе, имеет свою позицию, которая определяет ее вес или значение. Таким образом, каждая цифра вносит вклад в общую сумму числа, в зависимости от своей позиции.
Преимущества позиционной системы счисления заключаются в ее универсальности и простоте использования. С ее помощью можно записывать и обрабатывать числа любой величины, используя лишь ограниченный набор цифр. Это позволяет удобно выполнять арифметические действия над числами, а также передавать их в электронном виде.
Основы функционирования и принцип работы позиционной системы счисления
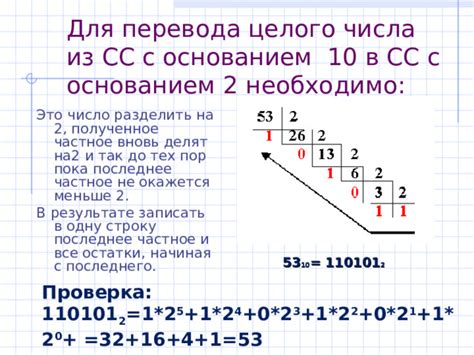
Позиционная система счисления представляет собой фундаментальный метод обозначения чисел, в котором значение каждого цифрового символа зависит от его позиции в числе. В этой системе каждая цифра может быть представлена с помощью конкретного символа или знака и иметь определенную весовую степень в зависимости от своей позиции. Такой подход к представлению чисел обеспечивает гибкость и эффективность в использовании различных основ, от двоичной системы до десятичной системы счисления и других.
Основной принцип работы позиционной системы счисления заключается в том, что каждая позиция в числе имеет весовую степень, которая определяет его значимость. Число разбивается на цифры, и каждая цифра имеет свое место, начиная с самой правой позиции, обозначаемой как единицы, и продолжая влево с возрастающими степенями следующих основ. Например, в десятичной системе весовые степени увеличиваются в десять раз с каждой позицией (1, 10, 100, 1000 и т. д.), в то время как в двоичной системе степени увеличиваются в два раза (1, 2, 4, 8 и т. д.).
Такой подход к представлению чисел в позиционной системе счисления позволяет легко выполнять математические операции, такие как сложение, вычитание, умножение и деление. Кроме того, благодаря своей удобной структуре и гибкости, позиционные системы счисления широко используются в компьютерной науке, информатике и других областях, где точность и эффективность вычислений играют важную роль.
Уникальный раздел: Основные выгоды практического использования позиционной системы счисления
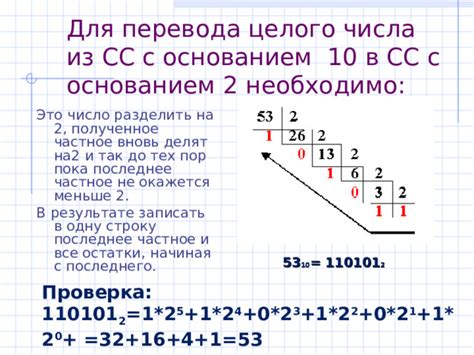
Это совершенно новый подход к записи чисел, в котором цифры в числе имеют разные степени значимости в зависимости от своего положения в числе. Система счисления учитывает вес цифр, а не только их значение. Таким образом, позиционная система позволяет компактно и удобно представлять большие числа с помощью всего нескольких символов.
Применение позиционной системы счисления обеспечивает ряд преимуществ, среди которых: экономия пространства, улучшенная читаемость чисел, возможность производить арифметические операции без необходимости выполнения сложных преобразований и обратные операции, такие как перевод из десятичной системы в позиционную и обратно. Более того, эта система также упрощает автоматизацию операций с числами и облегчает компьютерные вычисления.
Важным преимуществом позиционной системы счисления является то, что она является международным стандартом и широко применяется в нашей повседневной жизни, включая использование в компьютерных системах, финансовом секторе, инженерии и научных исследованиях. Это позволяет легче обмениваться информацией и выполнять вычисления, на основе единой и универсальной системы счисления.
Что может быть представлено в позиционной системе численности?

С помощью позиционной системы численности можно представлять числа различной величины и точности. Например, она позволяет записывать большие числа, состоящие из множества цифр, а также числа с десятичной дробной частью. Эта система также обладает гибкостью в выборе базы или основания системы счисления, что позволяет использовать ее в разных контекстах и областях знаний.
Многообразие чисел, которые можно представить в позиционной системе численности, позволяет эффективно работать с разными типами данных и выполнять различные математические операции. От простых вычислений до сложных механизмов, основанных на численности, позиционная система предоставляет мощный и универсальный инструмент для представления и обработки чисел.
- Целые числа - положительные и отрицательные значения без дробной части.
- Десятичные числа - числа с десятичной точкой, представленные в виде целой части и дробной части после точки.
- Двоичные числа - числа, состоящие только из двух цифр: 0 и 1.
- Восьмеричные числа - числа, состоящие из восьми цифр: 0, 1, 2, 3, 4, 5, 6 и 7.
- Шестнадцатеричные числа - числа, состоящие из шестнадцати цифр: 0-9 и A-F.
Это лишь небольшая часть множества чисел, которые можно представлять в позиционной системе счисления. Каждый тип числа имеет свои особенности и применения, отвечая на различные потребности и задачи.
История эволюции концепции позиционной системы отчетности

На протяжении многих столетий человечество стремилось создать универсальную систему счета, способную облегчить жизнь и упорядочить математические вычисления. И хотя существовали различные методы и системы, такие как римские цифры и многие другие, но они не были эффективными и понятными для широкого использования.
Спустя века и в результате совместного труда ученых и инженеров по всему миру, за исключением определенных ключевых компонентов, позиционная система счета была создана. Она основана на идее, что значение числа зависит от его положения в числе. Это означает, что одна и та же цифра может представлять разные значения в зависимости от ее позиции в числе.
Первыми в истории использующими этот метод были древние индийцы, которые впервые использовали позиционную систему для счета и записи чисел в II веке до нашей эры.
Затем, позиционная система древних индийцев дальше развивалась и распространялась на Востоке, где была принята и использовалась в Китае, Японии и других странах. Однако, в Западном мире эта система не была широко принята и использовалась до нескольких веков назад.
Окончательный прорыв в применении позиционной системы счета произошел в Средние века в Европе, когда были введены арабские цифры и нуль. В сочетании с этими новыми компонентами, позиционная система стала более удобной и эффективной для использования в различных областях, включая математику, науку и торговлю.
С тех пор позиционная система счисления продолжает развиваться и усовершенствоваться. Она стала неотъемлемой частью современного общества, широко используется во всех сферах деятельности, чтобы облегчить и упростить математические вычисления и счет.
Отличие позиционной системы счисления от других систем

В этом разделе мы рассмотрим ключевое отличие позиционной системы счисления от других систем, используемых для представления чисел. Позиционная система основана на уникальном принципе, который позволяет использовать несколько символов для обозначения чисел с разными разрядами. Это приводит к ряду существенных преимуществ, которые делают позиционную систему предпочтительной для многих задач.
- Гибкость и компактность: позиционная система позволяет представлять числа любой величины с помощью ограниченного набора символов. Простое добавление новых символов позволяет увеличить диапазон представимых чисел без изменения самой системы.
- Удобство математических операций: благодаря основе позиционной системы, арифметические операции над числами становятся намного проще и понятнее. Обратное действие, например, вычитание, также легко выполняется с использованием данной системы.
- Универсальность: позиционная система счисления применима для представления чисел в разных областях знаний, начиная от математики и физики, и заканчивая компьютерными науками и информационными технологиями.
- Простота восприятия и обучения: позиционная система счисления понятна и легко усваивается людьми с разными уровнями математической подготовки. Она основана на естественных и простых принципах, что делает ее доступной для всех.
Это лишь краткое описание отличий позиционной системы счисления от других систем. В следующих разделах мы более подробно рассмотрим принципы работы и преимущества использования этой системы, чтобы вы лучше поняли ее значение и широкое применение.
Примеры использования числовой системы в повседневной жизни
Эффективная коммуникация: В повседневной жизни мы часто сталкиваемся с необходимостью передавать и получать информацию, которая может быть представлена числами. Например, при общении о времени, дате, координатах местоположения или номерах телефонов. Использование позиционной системы счисления в этих случаях позволяет нам легко и однозначно передавать и понимать информацию.
Финансовые расчеты: В области финансов позиционная система счисления широко применяется для учета и анализа данных. Бухгалтеры, аналитики и инвесторы используют эту систему для работы с денежными стоями, акциями, процентными ставками и валютными курсами. Она позволяет проводить сложные расчеты, сравнивать и анализировать данные с высокой точностью и эффективностью.
Информационные технологии: Большая часть современных технологий основана на использовании позиционной системы счисления. Компьютеры, смартфоны, интернет - все это функционирует благодаря бинарной системе, которая является одной из разновидностей позиционной системы. Также многие алгоритмы и программы работают на основе математических операций с числами, которые представлены в этой системе, и с помощью нее происходит передача, хранение и обработка данных.
Маркетинг и статистика: В области маркетинга и статистики позиционная система счисления используется для анализа данных о покупках, продажах, клиентской активности и других показателях. Она помогает исследователям и аналитикам эффективно обрабатывать большие объемы информации, сравнивать результаты и прогнозировать тенденции.
Измерение и наука: Еще одна область жизни, где позиционная система счисления неотъемлема, - это измерение величин и научные исследования. Физики, химики, математики и другие ученые используют эту систему для представления и анализа данных, полученных в результате экспериментов и наблюдений. Она позволяет им точно и однозначно выражать результаты измерений и проводить дальнейшие расчеты и анализ.
Переход от одной системы счисления к другой: алгоритм и методика

В данном разделе рассмотрим процесс перевода чисел из одной системы счисления в другую, без углубления в специфические определения и детали. При осуществлении такого перевода необходимо применить определенный алгоритм и последовательность действий, чтобы успешно выполнить задачу и получить корректный результат. Методика перевода чисел из одной позиционной системы счисления в другую базируется на использовании математических операций и системы счисления с использованием различных значений позиций разрядов числа.
Исходя из заданного числа, необходимо определить исходную систему счисления и целевую систему счисления, в которую осуществляется перевод. Затем применяется специальный алгоритм, основанный на каждой позиции разряда числа и использующий значения позиции в исходной и целевой системе счисления.
| Исходная позиционная система счисления | Целевая позиционная система счисления | Алгоритм перевода |
|---|---|---|
| Двоичная система (2-ичная) | Десятичная система (10-ичная) | Применить формулу: сумма(цифра * 2^позиция) |
| Десятичная система (10-ичная) | Двоичная система (2-ичная) | Применить последовательное деление на 2 и полученные остатки являются разрядами числа |
| Шестнадцатеричная система (16-ичная) | Десятичная система (10-ичная) | Применить формулу: сумма(цифра * 16^позиция) |
| Десятичная система (10-ичная) | Шестнадцатеричная система (16-ичная) | Применить деление на 16 и полученные остатки представляются в виде соответствующих шестнадцатеричных цифр |
Таким образом, процесс перевода чисел из одной позиционной системы счисления в другую осуществляется с помощью применения определенного алгоритма, который зависит от исходной и целевой систем счисления. При соблюдении правил и последовательности действий можно получить корректный результат при переводе чисел между различными системами счисления.
Взгляд в будущее: тенденции и перспективы развития позиционной системы счисления

Представление чисел и выполнение вычислений в настоящее время осуществляется через использование позиционной системы счисления. Однако, будущее этой системы может претерпеть существенные изменения и принести новые тенденции и возможности для развития. В данном разделе будут рассмотрены перспективы, которые открываются перед позиционной системой счисления, а также изменения, которые можно ожидать в дальнейшем.
Вопросы, связанные с улучшением эффективности и повышением точности вычислений, играют важную роль в развитии позиционной системы счисления. Будущее может принести новые методы компактного представления чисел, что позволит сэкономить память и ускорить вычисления. Усовершенствование алгоритмов и появление новых математических методов может значительно повысить эффективность вычислительных процессов.
Одна из наиболее перспективных тенденций развития позиционной системы счисления – это интеграция с новыми технологиями и платформами. С развитием интернета вещей и мобильных устройств, позиционная система счисления может быть использована в новых областях, таких как смарт-города, автономные транспортные средства и умные дома. Это открывает новые возможности для применения позиционной системы счисления в сфере управления и контроля различных процессов.
Возможности развития позиционной системы счисления также простираются до области квантовых вычислений. Квантовая позиционная система счисления может быть использована в квантовых компьютерах, позволяя эффективно обрабатывать большие объемы данных и решать сложные задачи, которые для классических компьютеров могут быть неосуществимыми. Это открывает новые горизонты для развития вычислительной технологии и научных исследований.
Вопрос-ответ

Какова основа позиционной системы счисления?
Основой позиционной системы счисления является число, которое определяет количество различных цифр, используемых для представления чисел. Например, в десятичной системе счисления основа равна 10, так как мы используем десять цифр от 0 до 9.
Как работает позиционная система счисления?
Позиционная система счисления основана на том, что значение числа зависит от положения цифр в записи числа. Каждая цифра имеет определенное значение, которое определяется основой системы счисления и позицией цифры в числе. Например, в десятичной системе значение каждой цифры умножается на соответствующую степень десяти. Например, в числе 123 значение 1 равно 100, значение 2 равно 20, а значение 3 равно 3.
Какие преимущества имеет позиционная система счисления?
Позиционная система счисления имеет несколько преимуществ. Во-первых, она позволяет записывать и работать с числами любой величины. Во-вторых, она обладает простотой, так как основой системы задается натуральное число, и нет необходимости в использовании специальных символов или обозначений. В-третьих, позиционная система обеспечивает эффективное выполнение арифметических операций, так как для сложения и умножения чисел в этой системе используется один и тот же алгоритм для любых чисел.
Какая разница между позиционной системой счисления и непозиционной системой?
Главная разница между позиционной и непозиционной системами счисления заключается в способе представления чисел. В позиционной системе значение числа зависит от положения цифры в записи числа, в то время как в непозиционной системе каждая цифра имеет фиксированное значение, не зависящее от положения цифры. Например, в римской системе счисления цифра X всегда равна 10, независимо от положения цифры в числе.



