В мире геометрии есть множество движений и преобразований, которые позволяют установить расположение точек на единичной окружности. Эти методы нередко применяются в различных научных областях - от физики и математики до компьютерной графики и алгоритмов. Он позволяют нам изучить законы распределения точек, а также определить определенные закономерности, которые могут применяться в решении разнообразных задач.
Процесс определения расположения точек на единичной окружности требует некоторого шулерства и изобретательности. Ведь нам уже известно, что нельзя использовать прямые, очевидные способы решения. Поэтому, чтобы быть успешным в этой области, необходимо познакомиться с необычными методами и приемами, которые помогут нам добиться результата.
Например, для определения расположения точек можно использовать сравнительный анализ, исследовать феномены и явления, происходящие вокруг нас, а также проводить математические рассуждения на основе уже имеющихся данных. Такой подход позволит нам увидеть скрытые закономерности и взаимосвязи, которые ранее могли быть нам неочевидныmi.
Различные подходы к анализу положения точек на единичной окружности
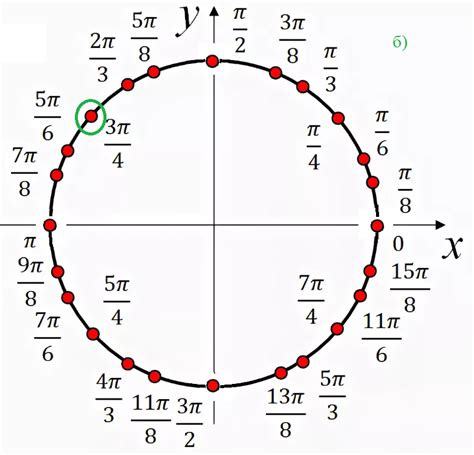
Данный раздел посвящен рассмотрению различных методов и подходов, применяемых для определения расположения точек на единичной окружности. В рамках исследования рассмотрены несколько алгоритмов, основанных на геометрических и численных принципах.
Один из подходов предусматривает использование геометрических методов, основанных на радиус-векторах и углах между точками и центром окружности. Рассматриваются сферические и плоские координаты, приводится формула нахождения угла между точками на окружности.
Кроме того, в статье рассмотрены численные методы, включающие аппроксимацию значений и использование математической статистики. Описывается применение многочленов Чебышева, метода наименьших квадратов и кластерного анализа для определения эффективного способа проверки положения точек.
| Метод | Описание |
|---|---|
| Геометрический метод | Основан на использовании радиус-векторов и углов для определения положения точек на окружности. |
| Численный метод | Включает аппроксимацию значений и использование эконометрических методов для определения положения точек. |
Измерение угла и косинуса для определения расположения точек на окружности
| Метод | Описание |
|---|---|
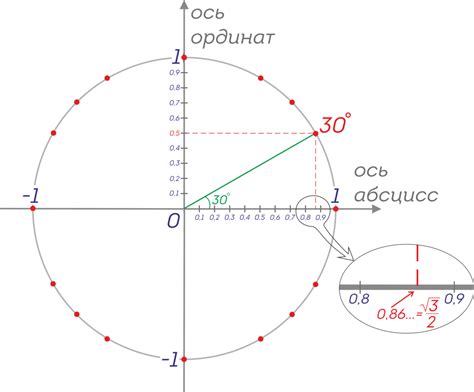
| Метод с использованием тригонометрии | Этот метод основан на применении тригонометрических функций, таких как синус и косинус. Он позволяет определить угол между начальным направлением и точкой на окружности, а также вычислить косинус этого угла. Зная косинус, мы можем определить координаты точки на окружности. |
| Метод геометрических построений | Этот метод применяет геометрические построения, такие как построение перпендикуляра и соединение точек на окружности с центром. Он позволяет определить угол между начальным направлением и точкой на окружности посредством измерения длин отрезков. Затем, используя косинус, мы можем определить координаты точки на окружности. |
| Метод использования геометрических фигур | Этот метод использует геометрические фигуры, такие как прямоугольный треугольник и прямоугольная система координат. Путем расчета угла и косинуса при помощи этих фигур, мы можем верно определить точки на единичной окружности. |
Использование указанных методов позволяет нам точно измерить угол и вычислить косинус для определения расположения точек на единичной окружности. Это особенно полезно при работе с геометрическими и физическими моделями, где точное знание координат точек критически важно.
Применение тригонометрических функций для оценки координат точек на единичной окружности
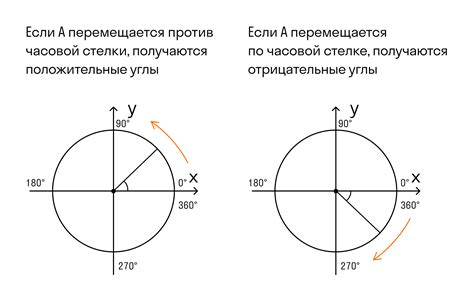
Тригонометрические функции, такие как синус (sin), косинус (cos) и тангенс (tan), могут быть использованы для оценки координат точек на окружности. Представление точек на окружности в виде углов и соответствующих им тригонометрических значений позволяет определить их положение относительно начального положения или другой точки на окружности.
Например, если нам дано значение угла α и радиус единичной окружности, мы можем использовать тригонометрические функции, чтобы найти координаты точки на окружности. Косинус угла α даст нам значение координаты по горизонтали, а синус угла α - значение координаты по вертикали. Используя эти значения, мы можем определить положение точки на окружности.
Вопрос-ответ

Какие методы можно использовать для проверки расположения точек на единичной окружности?
Для проверки расположения точек на единичной окружности можно использовать геометрический метод, аналитический метод и методы численного анализа. Геометрический метод включает в себя измерение углов и расстояний между точками на окружности. Аналитический метод основан на использовании алгебраических уравнений окружности и проверке их удовлетворения точками. Методы численного анализа позволяют аппроксимировать значения координат точек на окружности и сравнивать полученные результаты с ожидаемыми значениями.
Какие приемы помогут определить, что точки расположены на единичной окружности?
Для определения того, что точки расположены на единичной окружности, можно использовать приемы, основанные на свойствах окружности. Например, можно проверить, что все точки лежат на расстоянии 1 от центра окружности. Также можно проверить, что сумма квадратов координат точек равна 1. Другой прием - проверить, что все углы между точками равны 90 градусов. Использование уравнения окружности и сравнение полученных координат с ожидаемыми значениями также может помочь определить, что точки расположены на единичной окружности.
Какие инструменты можно использовать для проверки расположения точек на единичной окружности?
Для проверки расположения точек на единичной окружности можно использовать различные математические инструменты. Например, можно воспользоваться геометрическими инструментами, такими как линейка и угольник, для измерения расстояний и углов между точками. Также можно использовать компьютерные программы, которые позволяют анализировать координаты точек и применять математические методы для проверки их расположения на окружности. Для численного анализа можно использовать специальные программы и алгоритмы, позволяющие проводить аппроксимацию значений и сравнивать их с ожидаемыми значениями.



