В мире математики каждый объект имеет свое графическое представление. Графическое представление служит наглядной и интуитивно понятной формой визуализации различных математических концепций. В этой статье мы рассмотрим различия между графиками функций и графиками уравнений, а также углубимся в детали их анализа.
График функции и график уравнения - два основных понятия, которые широко используются в математике. Несмотря на то, что они оба представляют математические связи между переменными, их представление на графике имеет некоторые существенные отличия, которые стоит рассмотреть и проанализировать.
График функции, в отличие от графика уравнения, визуализирует зависимость между двумя переменными. Он позволяет представить изменение значений одной переменной в зависимости от значений другой переменной. График функции может быть представлен в виде кривой линии или графика функции, где по одной оси откладываются значения одной переменной, а по другой - значения другой переменной.
Определение понятий: функция и уравнение

В данном разделе мы рассмотрим основные понятия «функция» и «уравнение» и различия между ними. Они широко используются в математике и имеют особое значение в направлении синтеза аналитических моделей для описания явлений.
Функция является одним из фундаментальных понятий математики и представляет собой отображение между двумя множествами: исходным множеством, называемым областью определения, и целевым множеством, которое содержит значения, принимаемые функцией. Функция описывает зависимость между элементами этих множеств и позволяет получить соответствующий образ для каждого элемента исходного множества.
Уравнение, в свою очередь, является математическим представлением равенства двух выражений. Оно содержит неизвестное значение, которое требуется найти. Уравнение может быть алгебраическим или трансцендентным, в зависимости от его характера и свойств.
Главное различие между функцией и уравнением заключается в их цели. Функция служит для описания отношений и зависимостей между различными элементами, позволяя анализировать и предсказывать их поведение. Уравнение же направлено на решение задач и нахождение конкретных значений или корней.
Таким образом, функция и уравнение представляют разные подходы к манипулированию информацией в математическом контексте. Понимание и умение работать с этими концепциями играют важную роль в различных областях знания и позволяют решать широкий спектр задач.
Общий подход к созданию графиков функций и уравнений
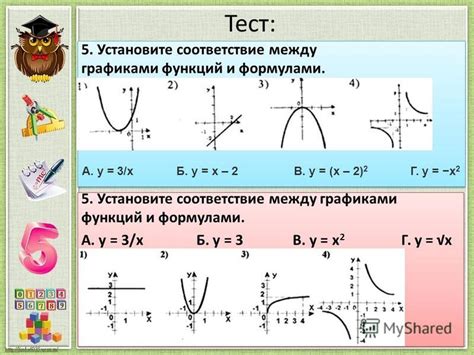
В данном разделе мы рассмотрим общие принципы и подходы к созданию графиков функций и уравнений, представляющие собой важный инструмент в анализе и визуализации математических моделей и данных.
При построении графиков следует учитывать основные характеристики функции или уравнения, такие как область определения, значения функции или уравнения в разных точках, а также их поведение на всей области определения. Для этого можно использовать различные методы и техники, такие как построение табличных значений, вычисление производных, анализ асимптот и экстремумов.
- Для построения графиков функций, можно использовать такие методы, как нахождение точек пересечения с осями координат, анализ знаков функции на разных участках, построение графиков производных и вторых производных, исследование монотонности функции и нахождение точек перегиба.
- При создании графиков уравнений, важно разбить уравнение на составляющие, анализировать их характеристики по отдельности, а затем собрать их вместе. Для этого могут быть полезны методы решения уравнений, построение графиков составных функций и использование геометрических методов, таких как нахождение точек пересечения и построение линий.
Важно помнить, что график функции и график уравнения являются взаимосвязанными понятиями, которые позволяют исследовать закономерности и взаимосвязи в математических моделях и данных. Четкое понимание общего подхода к их построению является важным инструментом для анализа и визуализации различных математических явлений.
Сравнение нотации графика функции и графика уравнения
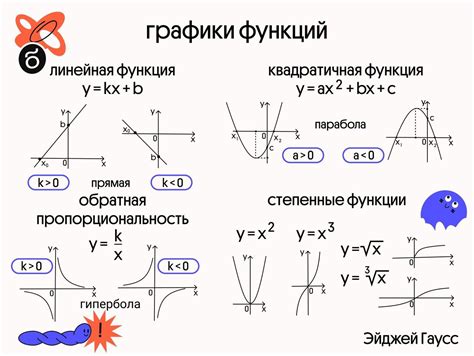
В данном разделе будут рассмотрены особенности и отличия в записи и представлении графиков функций и графиков уравнений. Рассмотрение будет основано на анализе разных видов записи математических объектов, их визуализации и смысловых аспектов.
График функции представляет собой графическое отображение зависимости одной переменной от другой. В отличие от уравнения, функция может быть записана с использованием различных символов и обозначений. Например, функция может быть представлена в виде аналитической формулы или графически с помощью графического редактора.
Однако, график уравнения имеет немного иной подход к представлению. Уравнение, в отличие от функции, записывается в виде равенства, связывающего две переменные или неизвестные. Нотация графика уравнения может варьироваться в зависимости от типа уравнения и используемых обозначений. График уравнения может быть представлен в виде кривой, линии или другой геометрической формы, соответствующей решению уравнения.
Таким образом, различия в нотации графика функции и графика уравнения связаны с особенностями записи и представления математических объектов. График функции выражает зависимость одной переменной от другой, в то время как график уравнения отражает взаимосвязь и решение уравнения. Понимание этих разностей поможет более точно интерпретировать представленные графики и использовать их в различных сферах науки и техники.
Интерпретация точек на графиках функции и уравнения

В данном разделе мы рассмотрим интерпретацию точек, которые встречаются на графиках функций и уравнений. Изучение этих точек поможет нам понять основные характеристики и свойства графиков, а также увидеть взаимосвязь между математическими моделями и их визуальным представлением.
Во-первых, точки на графике могут иметь различные положения относительно осей. Особое внимание следует обратить на точки пересечения графика с осями, которые называются корнями или нулями функции. Они являются решениями уравнения, соответствующего графику, и могут иметь важное значение при анализе функций и уравнений.
Во-вторых, мы будем изучать точки экстремума. Это точки, где график функции имеет локальный максимум или минимум. На графике уравнения точки экстремума могут представлять особые значения переменных, при которых достигается максимальное или минимальное значение функции. Разбираясь в этих точках, мы сможем понять, какие значения переменных приводят к экстремальным значениям функции или уравнения.
Кроме того, на графиках функций и уравнений можно встретить точки, где происходит изменение направления кривизны. Эти точки называются точками перегиба. Исследуя их положение на графике, мы можем понять, где происходит смена выпуклости или вогнутости. Это может быть полезно для анализа поведения функции или уравнения на разных участках.
Интерпретация точек на графиках функций и уравнений является важной задачей при изучении математических моделей. Это позволяет получить экспертное знание о свойствах функций и уравнений, а также использовать их для решения различных задач в науке, технике и других областях.
Учет особенностей функции при отображении ее на графике
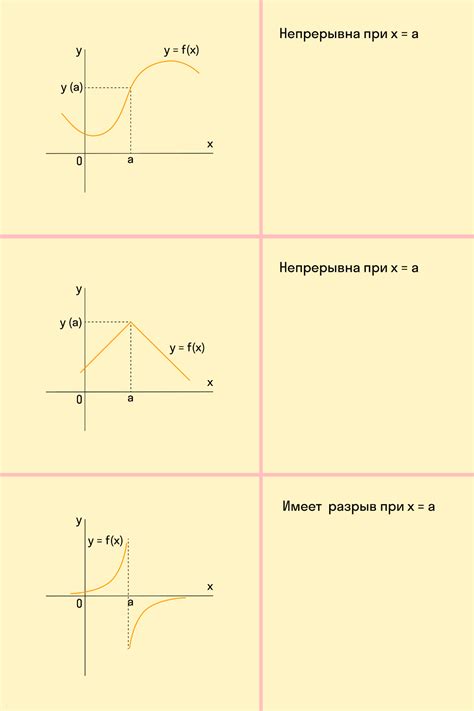
В этом разделе мы рассмотрим, как учет свойств функции влияет на построение ее графика. Каждая функция имеет свои уникальные особенности, которые можно учесть при визуализации ее поведения на графике.
Одна из важных характеристик функции - ее тип, который определяется видом алгебраического уравнения, связывающего зависимую и независимую переменные. Различные типы функций имеют разные свойства, которые могут быть выражены на графике. Например, графики линейных функций представляют собой прямые линии, а графики параболических функций имеют форму "U".
Кроме типа функции, также следует учитывать ее параметры и ограничения. Некоторые функции могут иметь вертикальные или горизонтальные асимптоты, которые нужно отобразить на графике. Изменение параметров функции, таких как сдвиги или масштабирование, также будет отражаться на графике.
Важным аспектом при построении графика функции является определение области определения и области значений. Кроме того, стоит учитывать особые точки, такие как точки перегиба, экстремумы и пересечения с осями координат. Использование различных стилей и цветов для выделения этих точек на графике может помочь визуализировать их значение.
Учет всех этих свойств функции при построении ее графика позволяет получить более точное представление о ее поведении и свойствах. Анализ графика функции помогает нам лучше понять ее сущность и использовать эту информацию для решения математических задач и принятия обоснованных решений в соответствующих областях науки и техники.
Важность уравнений в создании графиков
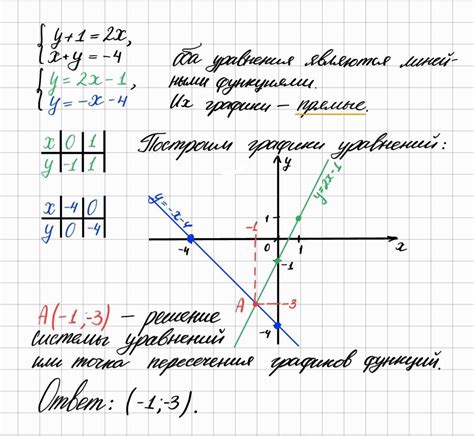
Раздел "Важность уравнений в создании графиков" рассматривает роль уравнений как важного инструмента при построении графиков различных функций и отображении их визуально. Уравнения представляют основу для определения формы и поведения графиков, позволяя увидеть взаимосвязь между независимой и зависимой переменными на плоскости.
В этом разделе будет рассмотрена значимость уравнений в процессе создания графиков, их влияние на представление информации о функциях, а также способы их использования для более глубокого анализа и понимания свойств функций. Рассмотрим различные методы и подходы к описанию уравнений и процесс их визуализации на графиках.
| Содержание раздела "Важность уравнений в создании графиков": |
| 1. Роль уравнений в представлении функций графически |
| 2. Преимущества использования уравнений при построении графиков |
| 3. Методы описания и интерпретации уравнений на графиках |
| 4. Визуализация видов уравнений на примере графиков |
| 5. Практическое применение уравнений в анализе графиков |
Использование графиков функций и уравнений в математическом анализе
В данном разделе мы рассмотрим применение графиков в математическом анализе и их значимость при изучении функций и уравнений. Графики представляют собой визуальное отображение математических объектов, которое позволяет уловить их особенности и взаимосвязи.
Графики функций и уравнений позволяют наглядно представить исследуемые объекты и анализировать их свойства. Они помогают определить области возрастания и убывания функций, находить максимумы и минимумы, а также выявлять особые точки, такие как точки перегиба или точки разрыва. Графики уравнений, в свою очередь, отображают геометрическое смысловое значение уравнений и позволяют найти их решения при помощи графического метода.
Использование графиков позволяет проводить анализ функций и уравнений с высокой степенью точности и удобством. Они служат отличным инструментом для нахождения величин, связанных с функциями и уравнениями, таких как производные, интегралы, приближенные значения и многое другое. Благодаря графикам, математическая аналитика становится более доступной и понятной, позволяя наглядно представить сложные математические концепции и теории.
| Преимущества использования графиков: | Примеры применения графиков в математическом анализе: |
|---|---|
| ✔️ Визуализация математических объектов | 📊 Построение графиков функций для определения их особенностей |
| ✔️ Обнаружение особых точек и экстремумов | 📈 Поиск решений уравнений с использованием графического метода |
| ✔️ Удобство проведения анализа функций и уравнений | 🔍 Определение значений производных и интегралов на графиках |
Изменение функции и уравнения: визуальное отображение
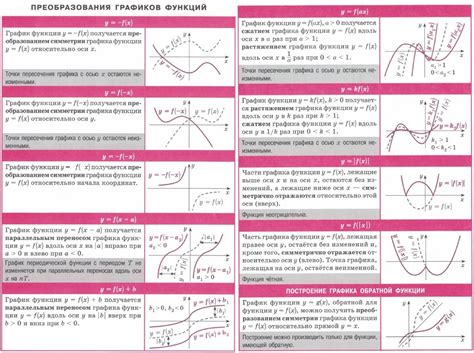
Этот раздел посвящен анализу способов визуального представления изменения функции и уравнения. Визуализация позволяет наглядно проследить тенденции и закономерности, связанные с этими математическими концепциями.
Ознакомление с визуальным представлением изменения функции и уравнения позволяет лучше понять их свойства и поведение. Визуализация может быть осуществлена в различных форматах, например, графическими диаграммами, графиками, диаграммами рассеяния, плотностями вероятности и другими методами, отобранными с учетом специфики функции или уравнения.
Кроме того, визуализация позволяет сравнить различные функции и уравнения, а также выделить особенности их изменения. Она может помочь идентифицировать точки пересечения, экстремумы, асимптоты и другие важные характеристики, которые служат ключевыми моментами в анализе функции или уравнения.
Конечно, визуальное представление изменения функции и уравнения не заменяет математические методы и формулы, однако оно является мощным инструментом для иллюстрации и подтверждения результатов анализа. Объединение визуализации и анализа данных позволяет получить более полное представление о поведении функции и уравнения и облегчает интерпретацию их свойств.
Роль графиков функции и уравнения в научных и прикладных исследованиях

В данном разделе мы рассмотрим возможности и применение графиков функции и уравнения в научных и прикладных исследованиях. Детальный анализ позволит выявить уникальные способы использования их в практике, а также показать, как они способствуют уточнению и визуализации результатов исследований.
Вопрос-ответ

Какие основные отличия между графиком функции и графиком уравнения?
График функции представляет собой множество всех упорядоченных пар, состоящих из аргумента и значения функции. График уравнения, в свою очередь, представляет собой множество точек, которые удовлетворяют данному уравнению. Основное отличие заключается в том, что функция может иметь бесконечное количество точек на графике, в то время как график уравнения может быть конечным или содержать изолированные точки.
Какая связь между графиком функции и графиком уравнения?
График функции и график уравнения имеют тесную связь. Если уравнение представляет собой явное выражение функции вида y = f(x), то его график будет совпадать с графиком функции. Однако, уравнение может быть неявным, то есть записанным в виде F(x,y) = 0. В этом случае график уравнения показывает множество точек, которые удовлетворяют условию F(x,y) = 0, и может не полностью совпадать с графиком функции.
Какие еще различия можно выделить между графиком функции и графиком уравнения?
Еще одно отличие между графиком функции и графиком уравнения заключается в их интерпретации. График функции представляет собой визуализацию зависимости между аргументом и значением функции. Он может использоваться для анализа поведения функции и выявления ее основных характеристик, таких как интервалы возрастания и убывания, экстремумы и точки перегиба. График уравнения, в свою очередь, может использоваться для решения задач, связанных с поиском точек пересечения двух графиков или нахождением решений уравнения.
Какие уточнения нужны при анализе графиков функций и уравнений?
При анализе графиков функций и уравнений важно учитывать допустимые значения аргументов и возможные ограничения уравнений. Например, функции могут иметь ограниченные или неограниченные области определения, что может отразиться на их графиках. Также, при рассмотрении графиков уравнений стоит учитывать условия, которые могут ограничивать диапазоны значений аргументов или функции в уравнении.



