Кривой отрезок – понятие, которое широко используется в математике для описания кривых линий или отрезков между двумя точками на плоскости или в пространстве. Кривой отрезок может быть прямым или изогнутым, иметь различные формы и характеристики, и играет важную роль в геометрии и анализе.
Важным свойством кривого отрезка является его длина, которая определяется геометрически и может быть выражена с помощью математических формул. Кривой отрезок может быть задан как аналитически, так и графически, что позволяет изучать его свойства и использовать в различных математических задачах.
В данной статье мы рассмотрим определение кривого отрезка, приведем примеры его видов и форм, а также обсудим основные свойства и связанные с ним концепции в математике.
Что такое кривой отрезок
Определение кривого отрезка в математике
Примеры кривых отрезков в геометрии
Кривой отрезок может представлять собой следующие геометрические фигуры:
1. Окружность: кривой отрезок, который состоит из всех точек, равноудаленных от центра данной окружности.
2. Элипс: кривой отрезок, образуемый пересечением плоскости и поверхности, у которой сумма расстояний до двух фокусов постоянна.
3. Парабола: кривой отрезок, который определяется уравнением y = x^2 и имеет форму асимптотической кривой.
4. Гипербола: кривой отрезок, образуемый пересечением плоскости и поверхности, у которой разность расстояний до двух фокусов постоянна.
Свойства кривых отрезков на плоскости
1. Произвольные точки: Кривой отрезок может быть определен произвольно от одной точки до другой на плоскости.
2. Прямолинейность: Кривой отрезок всегда является прямолинейным отрезком, не имеющим кривизны.
3. Ориентация: Кривой отрезок имеет фиксированное направление и ориентацию между начальной и конечной точками.
4. Длина: Длина кривого отрезка может быть вычислена по формуле длины прямой между начальной и конечной точками.
Как определить длину кривого отрезка

Длину кривого отрезка можно определить с помощью интеграла. Если у нас есть функция \( f(x) \), заданная на отрезке \( [a, b] \), то длину кривого отрезка можно найти по формуле:
\[ L = \int_{a}^{b} \sqrt{1 + [f'(x)]^2} \, dx \]
Таким образом, чтобы определить длину кривого отрезка, нужно сначала найти производную функции \( f(x) \), затем взять корень из суммы квадратов производной и единицы, а затем проинтегрировать это выражение по заданному отрезку. Полученное значение будет являться длиной кривого отрезка.
Связь кривого отрезка с дугой на плоскости
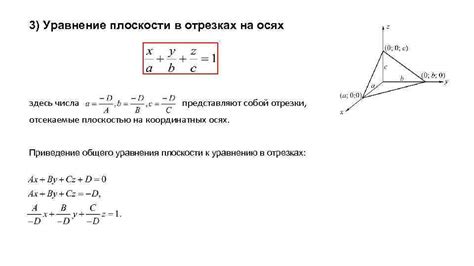
Как правило, кривая отрезка и дуга имеют одинаковую форму и описывают одно и то же пространство. Связь между ними проявляется в геометрических свойствах и характеристиках, таких как длина, радиус кривизны и т.д.
Изучение связи кривого отрезка с дугой позволяет понять особенности и свойства кривых на плоскости, что является важным для решения задач в математике и других науках.
Графическое изображение кривого отрезка в координатной плоскости
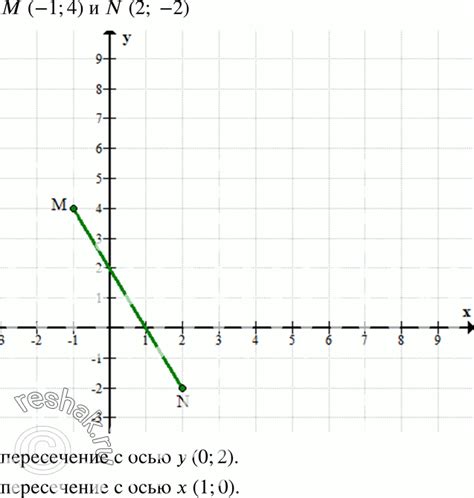
Для графического изображения кривого отрезка на координатной плоскости, нам нужно задать две конечные точки A(x₁, y₁) и B(x₂, y₂). Затем проведем прямую, проходящую через эти две точки. Эта прямая и будет представлять собой кривой отрезок от точки A до точки B.
Кривой отрезок изображается на плоскости линией, которая соединяет точки A и B. При этом прямая, являющаяся кривым отрезком, не имеет разрывов и уклонов, что отличает его от других видов кривых.
Пример графического изображения кривого отрезка можно увидеть на координатной плоскости, где заданы точки A(1, 2) и B(4, 6), и соединены прямой линией, образуя кривой отрезок между этими двумя точками.
| Точка A | (1, 2) |
| Точка B | (4, 6) |
Вопрос-ответ

Что такое кривой отрезок в математике?
Кривой отрезок в математике - это линейный отрезок, соединяющий две точки на плоскости или в пространстве. Этот отрезок может принимать любую форму, включая кривые и петли.
Какие свойства имеет кривой отрезок?
Кривой отрезок обладает свойствами, характерными для отрезка: он имеет начало и конец в виде двух точек, может принимать любое положение в пространстве, быть криволинейным и иметь направление.
Можете привести пример кривого отрезка в математике?
Для примера кривого отрезка можно взять дугу окружности, соединяющую две ее точки. Этот отрезок будет иметь изгиб и форму дуги, сохраняя при этом свою линейность.



