Иррациональные числа всегда были объектом внимания математиков и философов. Они вызывали удивление и недоумение своей непостоянной десятичной дробной частью, не имеющей периода. Они казалиссь чем-то загадочным и необычным, порой вызывая даже страх перед неизведанным.
Однако в последние годы подход к иррациональным числам начал меняться. Современные математики утверждают, что понимание и использование иррациональных чисел является неотъемлемой частью математики и науки в целом. Эти числа играют ключевую роль в различных областях, от алгебры до геометрии, от физики до программирования.
Опровергнуто лишь иостигматическое восприятие об иррациональных числах. Они перестали быть объектом недоумения и страха, став, напротив, важным инструментом для понимания и описания мира. Их красота и сложность раскрывают новые горизонты для науки, вдохновляя умы исследователей по всему миру.
Опровержение мифа об иррациональных числах
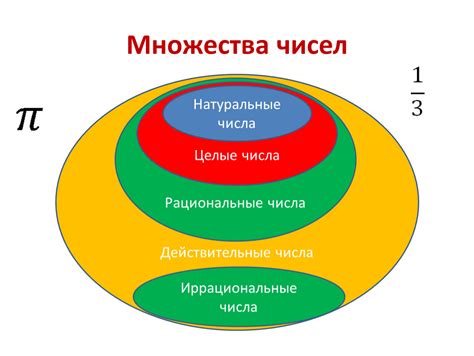
Иррациональные числа могут быть представлены как десятичные дроби с бесконечным количеством знаков после запятой. Это свойство делает их особенными и позволяет использовать их для моделирования сложных математических явлений.
Роль иррациональных чисел в математике

Иррациональные числа играют ключевую роль в математике, расширяя понимание мира и предоставляя нам инструменты для решения разнообразных задач. Они дополняют рациональные числа, делая математические вычисления более гибкими и точными. Иррациональные числа встречаются в различных областях науки, от геометрии до физики, а также используются в цифровой криптографии и других прикладных задачах.
Иррациональные числа обладают удивительными свойствами, такими как непрерывность дробной части, отсутствие периодичности и невозможность представления в виде простой дроби. Их иррациональность позволяет нам понимать и описывать сложные математические явления и является основой для развития новых математических теорий и методов.
Вопрос-ответ

Чем отличаются иррациональные числа от рациональных?
Иррациональные числа не могут быть представлены в виде дроби, у них бесконечное непрерывное десятичное представление без периодичности. В то время как рациональные числа могут быть представлены в виде дроби с конечным или периодическим десятичным разложением.
Почему иррациональные числа существуют?
Иррациональные числа существуют, потому что не все числа можно представить в виде простой дроби. Например, корень из 2 является иррациональным числом, и его нельзя записать как обыкновенную дробь. Такие числа возникают при решении уравнений, когда рациональных решений не существует.
Есть ли практическое применение для иррациональных чисел?
Иррациональные числа имеют широкое применение в различных областях, включая математику, физику, экономику и технику. Например, они используются при построении сложных математических моделей, в финансовых расчетах, при проектировании алгоритмов и т.д.
Могут ли иррациональные числа быть представлены в компьютере?
Иррациональные числа не могут быть точно представлены в компьютере из-за их бесконечной дробной части. Обычно в компьютере используются приближенные значения иррациональных чисел с определенной точностью, что может привести к погрешностям в вычислениях.



