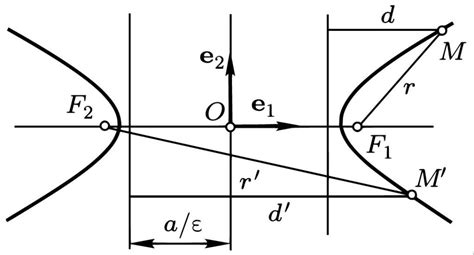
Гипербола – это геометрическое место точек плоскости, для которых модуль разности расстояний до двух фиксированных точек, называемых фокусами, постоянен и равен заданному числу. Гиперболу можно задать уравнением в декартовых координатах, которое обычно выражается в виде дробно-линейной функции.
Оси координатной плоскости являются важными элементами геометрии, образуя пересечения в начале координат и разделяя плоскость на четверти. Но возникает вопрос: пересекает ли гипербола оси координатной плоскости? Ответ на этот вопрос зависит от положения и ориентации гиперболы относительно осей координат.
Что такое гипербола?

Гипербола не пересекает ни ось x, ни ось y координатной плоскости.
Как задается гипербола на плоскости?

Гипербола на плоскости задается уравнением вида:
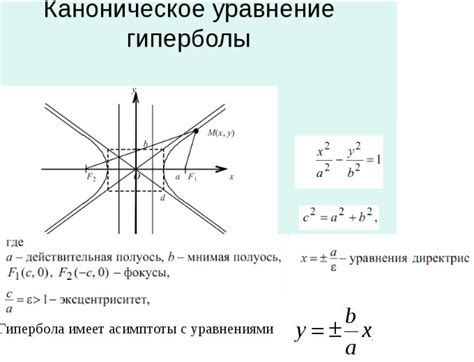
| (x - h)^2/ a^2 - (y - k)^2/ b^2 = 1 |
где (h, k) - координаты центра гиперболы, a и b - параметры, определяющие размеры гиперболы. Если a>b, то гипербола расположена вдоль оси x, если a
Гипербола всегда имеет две асимптоты, которые определяют ее форму и направление распределения.
Понятие пересечения гиперболы с осями координат
Гипербола, как и другие кривые второго порядка, может пересекать оси координатной плоскости. При этом пересечение гиперболы осью абсцисс (OX) происходит в точках, где уравнение гиперболы принимает вид y = 0, т.е. когда значение y равно нулю. Аналогично, гипербола пересекает ось ординат (OY) в точках, где уравнение гиперболы принимает вид x = 0, т.е. когда значение x равно нулю. Такие точки пересечения с осями координат могут быть использованы для определения поведения и особенностей гиперболы на координатной плоскости.
Как выглядит пересечение гиперболы с осью абсцисс?

Если уравнение гиперболы равно x^2/a^2 - 0 = 1, то получаем x^2/a^2 = 1, откуда x = ±a. Таким образом, пересечение гиперболы с осью абсцисс происходит в точках (a,0) и (-a,0).
Как выглядит пересечение гиперболы с осью ординат?

x^2/a^2 = 1
x^2 = a^2
x = ±a
Таким образом, пересечение гиперболы с осью ординат состоит из двух точек: (a, 0) и (-a, 0).
Существует ли пересечение гиперболы с обеими осями?

Гипербола не пересекает ни ось абсцисс (ось x), ни ось ординат (ось y). Однако, она может иметь точки пересечения с этими осями, если уравнение гиперболы позволяет это. Например, если значение a или b равно нулю, гипербола становится центрированной на одной из осей и пересекает ее.
Правила определения пересечений гиперболы и осей координат
Гипербола может пересечь оси координатной плоскости в точках, которые называются вершинами. Правила определения пересечений гиперболы и осей координат зависят от положения гиперболы относительно осей.
| Положение гиперболы | Условия пересечения |
|---|---|
| Гипербола с вертикальной осью | При пересечении оси x, y = 0 |
| Гипербола с горизонтальной осью | При пересечении оси y, x = 0 |
Влияние параметров на пересечение гиперболы с осями
Пересечение гиперболы с осями координатной плоскости зависит от значений параметров уравнения гиперболы. Рассмотрим различные случаи:
| Параметры | Попадание на ось x | Попадание на ось y |
|---|---|---|
| а > b | Не пересекает | Пересекает |
| a = b | Не пересекает | Не пересекает |
| a | Пересекает | Не пересекает |
Таким образом, параметры a и b гиперболы влияют на то, пересекает ли гипербола оси координатной плоскости.
Эксперименты для демонстрации пересечений гиперболы
Для наглядной демонстрации пересечений гиперболы с осями координатной плоскости можно провести следующие эксперименты:
1. Нарисовать гиперболу на координатной плоскости и проанализировать ее уравнение, чтобы определить, пересекает ли гипербола оси координат.
2. Найти координаты точек пересечения гиперболы с осями (если они есть) путем решения системы уравнений.
3. Провести вычисления и построить график искомой гиперболы, чтобы визуально убедиться в правильности расчетов.
4. Изучить особенности пересечения гиперболы с осями координатной плоскости и сравнить результаты с общепринятыми теоретическими представлениями.
Вопрос-ответ

Пересекает ли гипербола оси координатной плоскости?
Гипербола может пересекать обе оси координатной плоскости, в зависимости от её эксцентриситета и положения центра относительно осей. Если гипербола центрирована в начале координат или далеко от них, то она может пересечь обе оси. В противном случае, гипербола может не пересекать оси.
Как можно определить, пересекает ли гипербола оси координатной плоскости?
Для определения пересечения гиперболы с осями координатной плоскости необходимо вычислить коэффициенты уравнения гиперболы и проанализировать их знаки. Если уравнение гиперболы содержит перемещение центра и эксцентриситет, то можно определить, пересечет ли она оси координат.
Может ли гипербола не пересекать оси координатной плоскости?
Да, гипербола может не пересечь какую-либо из осей координатной плоскости, если её центр находится достаточно далеко от оси или если эксцентриситет равен единице. Это означает, что касательные к гиперболе будут параллельны оси, и сама гипербола не будет пересекать их.
Что делать, если гипербола пересекает оси координатной плоскости?
Если гипербола пересекает оси координатной плоскости, это означает, что она может иметь точки пересечения с осями. В этом случае можно вычислить эти точки, используя уравнение гиперболы и подставив соответствующие значения координат.



