Квадрат, описанный вокруг окружности, представляет собой геометрическую фигуру, у которой стороны параллельны осям координат и диагонали этого квадрата равны диаметру окружности. В этой статье мы рассмотрим формулу для вычисления площади квадрата, описанного вокруг заданной окружности, а также приведем простые примеры для наглядного понимания данной геометрической задачи.
Для нахождения площади квадрата, описанного вокруг окружности, мы можем воспользоваться следующей формулой: S = 2r^2, где S - площадь квадрата, r - радиус заданной окружности. Эта формула обусловлена геометрическими свойствами квадрата и окружности, что позволяет нам легко найти площадь данной фигуры.
Площадь квадрата, описанного вокруг окружности
Площадь квадрата, описанного вокруг окружности, можно выразить через радиус окружности. Если радиус окружности равен r, то сторона квадрата равна 2r (диаметр окружности). Площадь квадрата можно найти по формуле s = (2r)^2 = 4r^2.
Например, если радиус окружности равен 5 см, то сторона квадрата будет 10 см, а его площадь равна 100 квадратным сантиметрам (100 см²).
Что такое квадрат?

Квадрат – одна из базовых фигур в геометрии, которая широко используется в математике, инженерии, архитектуре и других областях. Отличительной особенностью квадрата является его простота и регулярная форма, которая позволяет легко вычислять его характеристики, такие как площадь, периметр и диагональ.
Формула для нахождения площади
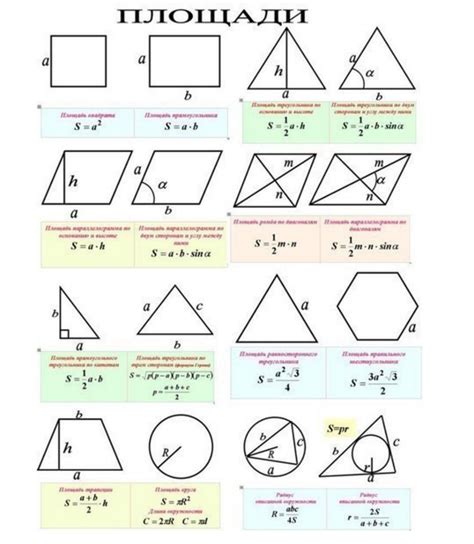
Для нахождения площади квадрата, описанного вокруг окружности, можно воспользоваться следующей формулой:
| Площадь квадрата | : | 4 * (Площадь окружности) |
Способы решения задачи

Примеры расчетов

Пример 1:
- Дана окружность с радиусом R=5 см.
- Найдем площадь квадрата, описанного вокруг этой окружности.
- Сначала найдем диагональ квадрата: D = 2R = 10 см.
- Площадь квадрата равна D^2/2 = 10^2/2 = 100/2 = 50 см^2.
Ответ: Площадь квадрата, описанного вокруг окружности с радиусом 5 см, равна 50 см^2.
Пример 2:
- Дана окружность с радиусом R=8 м.
- Найдем площадь квадрата, описанного вокруг этой окружности.
- Диагональ квадрата: D = 2R = 16 м.
- Площадь квадрата равна D^2/2 = 16^2/2 = 256/2 = 128 м^2.
Ответ: Площадь квадрата, описанного вокружности с радиусом 8 м, равна 128 м^2.
Практическое применение в задачах

Площадь квадрата, описанного вокруг окружности, имеет непосредственное применение в геометрии и различных математических задачах. Например, данная формула может использоваться при решении задач, связанных с построением круговой дороги вокруг парка или участка земли, чтобы максимально эффективно использовать площадь.
Также данная концепция может быть использована при проектировании различных объектов, когда необходимо определить минимальную площадь квадрата, способного вместить окружность определенного диаметра. Использование формулы позволит оптимизировать распределение площади и ресурсов.
Вопрос-ответ

Какая формула площади квадрата, описанного вокруг окружности?
Площадь квадрата, описанного вокруг окружности равна удвоенной площади окружности. Формула выглядит так: S = 2πr^2, где r - радиус окружности.
Как решить задачу о площади квадрата, который описан вокруг окружности с заданным радиусом?
Для решения задачи нужно найти радиус окружности, затем подставить его в формулу площади квадрата, описанного вокруг окружности (S = 2πr^2) и вычислить площадь квадрата.
Можете привести пример расчета площади квадрата, который описан вокруг окружности с радиусом 5 см?
Для окружности с радиусом 5 см площадь квадрата, описанного вокруг нее, равна 2π(5)^2 = 2π(25) = 50π см^2.
Какую пользу можно извлечь из знания формулы для площади квадрата, описанного вокруг окружности?
Зная эту формулу, можно быстро и легко вычислить площадь квадрата, если известен радиус окружности. Также это позволяет решать различные задачи, связанные с геометрией и расчетами площадей фигур.



