Пифагорова теорема - одно из самых известных математических утверждений, которое знакомо каждому школьнику. Она гласит, что для прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Но почему эта теорема так важна и интересна?
Пифагорова теорема открывает перед нами удивительный мир геометрии, позволяя понять взаимосвязи между сторонами прямоугольного треугольника. Интересно, что название этой теоремы отражает величину, которая лежит в ее основе - долгое время ее считали магическим заклинанием, приносящим успех и удачу в математике.
Понимание Пифагоровой теоремы позволяет нам не только решать задачи на построение и вычисление сторон треугольников, но и видеть гармонию и прекрасный порядок в математическом мире. Эта теорема - как открытие новой страны, где правят порядок, пропорции и равновесие.
Почему Пифагорова теорема так называется
Пифагорова теорема была названа в честь древнегреческого математика Пифагора, который жил в VI веке до н.э. и считается основателем пифагорейской школы.
Пифагорова теорема утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Это важное математическое утверждение получило имя Пифагора в честь его открытия и активного изучения этого факта.
История создания и название

Пифагорова теорема, названная в честь древнегреческого математика Пифагора, была открыта и доказана им в VI веке до н.э. Пифагор был основателем пифагорейской школы, где математика играла важную роль. Теорема стала одним из самых известных математических утверждений и была первоначально сформулирована в контексте геометрических и числовых закономерностей.
Математический смысл и значение

| Катет 1 | Катет 2 | Гипотенуза |
| а | б | с |
Суть теоремы заключается в том, что существует определенная зависимость между длинами сторон прямоугольного треугольника. Пифагорова теорема можно применить не только в геометрии, но и в других областях математики, физики и техники. Этот результат имеет большое практическое значение и часто используется в различных задачах, связанных с измерениями, расчетами и доказательствами.
Свойства прямоугольного треугольника по Пифагору

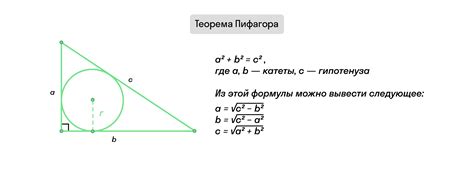
По теореме Пифагора для прямоугольного треугольника с катетами a и b, и гипотенузой c, верно следующее утверждение:
- Сумма квадратов катетов равна квадрату гипотенузы: \(a^2 + b^2 = c^2\).
- Это свойство позволяет нам вычислять длину одного из катетов или гипотенузы, если известны два других значения.
Отношения длин сторон треугольника
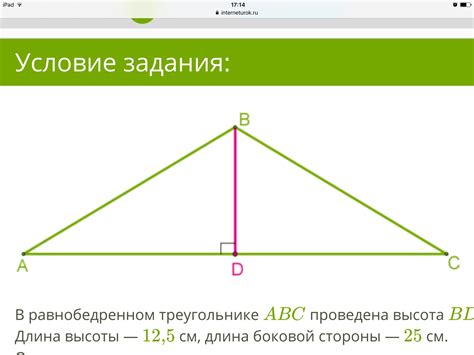
В треугольнике справедливы следующие отношения между длинами его сторон:
1. Сумма длин двух сторон треугольника всегда больше длины третьей стороны:
Если a, b, и c - стороны треугольника, то a + b > c, a + c > b и b + c > a.
2. Разность длин двух сторон треугольника всегда меньше длины третьей стороны:
Если a, b, и c - стороны треугольника, то |a - b|
3. Отношения длин сторон в прямоугольном треугольнике связаны с Пифагоровой теоремой:
Если a и b - катеты прямоугольного треугольника, а c - гипотенуза, то a^2 + b^2 = c^2.
Геометрическое доказательство

Площадь квадрата C равна сумме площадей треугольников A и B (по теореме Пифагора): C = A + B.
Площадь квадрата C можно представить как (a + b)^2, а сумму площадей треугольников A и B как a^2 + b^2.
Таким образом, получаем равенство: (a + b)^2 = a^2 + b^2, что является геометрическим доказательством Пифагоровой теоремы.
Аналогии Пифагоровой теоремы
1. Теорема Пифагора в геометрии: Прямоугольный треугольник, в котором квадрат гипотенузы равен сумме квадратов катетов, аналогичен уравнению в математической формуле.
2. Пифагорова теорема в физике: Принцип сохранения энергии в физике напоминает Пифагорову теорему - энергия в начале равна сумме энергий в конце.
3. Пифагорова теорема в музыке: Звуки, образующие гармонию, соответствуют отношениям чисел в треугольнике, аналогия с теоремой Пифагора.
Вопрос-ответ

Почему в геометрии Пифагорова теорема называется так же, как и ученый Пифагор?
Теорема названа в честь древнегреческого математика Пифагора, который первым доказал это утверждение. Однако, стоит отметить, что подобные правильные треугольники известны были и до Пифагора.
Почему все стороны в прямоугольном треугольнике равны?
В прямоугольном треугольнике Пифагорова теорема утверждает, что квадрат гипотенузы (стороны наибольшей) равен сумме квадратов катетов (остальных двух сторон). Таким образом, по формуле a^2 + b^2 = c^2 все стороны будут равны при выполнении данного условия.
Как объяснить Пифагорову теорему простыми словами?
Пифагорова теорема утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. То есть, сумма площадей квадратов на двух меньших сторонах равна площади квадрата на гипотенузе.
Какая геометрическая формула лежит в основе Пифагоровой теоремы?
Пифагорова теорема опирается на геометрическую формулу, которая утверждает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Формула выглядит как a^2 + b^2 = c^2, где a и b - длины катетов, а c - длина гипотенузы.
Почему Пифагорова теорема так важна в математике?
Пифагорова теорема является одной из основных теорем в геометрии и математике в целом. Она позволяет находить длины сторон треугольника, зная только длины двух из них, и является основой для применения теоремы в различных задачах и вычислениях.



