Матрица - это один из основных объектов линейной алгебры, который используется для представления систем линейных уравнений или преобразований пространства. Приведение матрицы к диагональному виду имеет важное значение как в теории, так и в практике.
Когда матрица приведена к диагональному виду, все элементы вне главной диагонали равны нулю. Это значит, что система уравнений (если матрица используется для их решения) становится гораздо проще и понятнее.
Приведение матрицы к диагональному виду также упрощает вычисления, улучшает понимание структуры данных и позволяет эффективнее применять методы решения задач линейной алгебры. Поэтому овладение навыком работы с матрицами в диагональном виде существенно повышает профессиональную компетентность в области математики и информационных технологий.
Польза диагональной матрицы
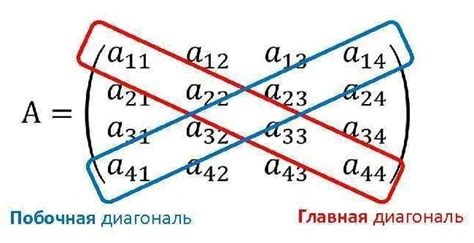
- Упрощение вычислений: в диагональной матрице все операции с элементами сводятся к умножению и делению на диагональные элементы, что упрощает вычисления.
- Облегчение анализа систем уравнений: при решении систем линейных уравнений диагональная матрица позволяет эффективно применять метод Гаусса и другие алгоритмы.
- Улучшение производительности: в некоторых задачах, таких как умножение матриц, использование диагональных матриц может значительно повысить скорость вычислений.
- Снижение размерности: диагональная матрица подразумевает, что большинство элементов равны нулю, что позволяет снизить размерность данных и уменьшить объем вычислений.
Удобство в вычислениях
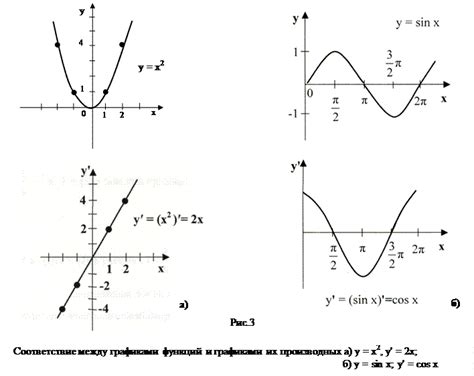
Приведение матрицы к диагональному виду существенно упрощает различные вычисления и операции над матрицей. Диагональная матрица обладает свойством того, что все элементы вне главной диагонали равны нулю, что делает её структуру более простой и понятной для анализа.
При выполнении операций с диагональной матрицей, таких как сложение, умножение и взятие обратной матрицы, математические действия становятся значительно более легкими и эффективными. Благодаря преобразованию матрицы к диагональному виду, можно существенно упростить вычисления и избежать излишних трудностей.
| 3 | 0 | 0 |
| 0 | 4 | 0 |
| 0 | 0 | 5 |
Улучшение эффективности

Приведение матрицы к диагональному виду играет важную роль в повышении эффективности вычислений. Когда матрица становится диагональной, упрощается проведение операций с ней, таких как умножение, сложение и нахождение обратной матрицы. Это позволяет сократить время вычислений и улучшить общую производительность алгоритмов, использующих данную матрицу.
Благодаря диагонализации матрицы можно также легче отслеживать зависимости и взаимосвязи между ее элементами, что способствует более глубокому анализу данных и принятию обоснованных решений на основе матричных операций.
Повышение точности данных

Приведение матрицы к диагональному виду играет ключевую роль в повышении точности данных. Данный процесс позволяет выделить основные характеристики и представляет данные в более удобном и понятном виде. Когда матрица приведена к диагональному виду, становится легче обнаружить взаимосвязи между различными переменными, что помогает в анализе данных и принятии обоснованных решений. Благодаря преобразованию матрицы к диагональному виду, мы можем получить более точные и достоверные результаты исследований, что важно для принятия важных решений и оптимизации бизнес-процессов.
Снижение сложности задач
Приведение матрицы к диагональному виду играет важную роль в задачах линейной алгебры. Когда матрица приводится к диагональному виду, это упрощает вычисления и позволяет изучать её с большей точностью. Например, для матрицы в диагональном виде легко найти собственные значения и векторы, что значительно снижает сложность решения систем уравнений и других задач.
| 1 | 0 | 0 |
| 0 | 2 | 0 |
| 0 | 0 | 3 |
Приведение матрицы к диагональному виду также помогает в оптимизации вычислений и улучшении производительности алгоритмов, особенно при работе с большими объемами данных. Это позволяет экономить время и ресурсы при решении задач в различных областях, от науки и техники до финансов и машинного обучения.
Оптимизация математических операций

Приведение матрицы к диагональному виду имеет важное значение для оптимизации математических операций. Диагональная матрица обладает особым свойством: при умножении матрицы на диагональную матрицу результатом будет матрица, у которой каждая строка умножена на соответствующий элемент диагональной матрицы. Это позволяет существенно упростить вычисления и ускорить процесс обработки данных.
Приведение матрицы к диагональному виду позволяет сократить количество операций в сложных алгоритмах, улучшить производительность вычислений и упростить интерпретацию результатов. Таким образом, оптимизация математических операций через приведение матрицы к диагональному виду является важным этапом при работе с линейной алгеброй и матричными операциями.
| Преимущества оптимизации матричных операций: |
| 1. Увеличение скорости вычислений за счет уменьшения количества операций. |
| 2. Улучшение производительности при работе с большими объемами данных. |
| 3. Уменьшение затрат времени и ресурсов на выполнение сложных математических алгоритмов. |
Вопрос-ответ

Зачем нужно приводить матрицу к диагональному виду?
Приведение матрицы к диагональному виду имеет ряд преимуществ. Во-первых, в диагональной матрице все элементы вне главной диагонали равны нулю, что упрощает вычисления и анализ. Во-вторых, диагональная матрица обладает удобными свойствами при умножении и нахождении обратной матрицы. Кроме того, диагональные матрицы часто используются в прикладной математике для упрощения систем линейных уравнений и задач оптимизации.
Каким образом можно привести матрицу к диагональному виду?
Матрицу можно привести к диагональному виду с помощью различных методов, таких как метод Гаусса или методы преобразования Жордана и Шура. Один из способов – это диагонализация матрицы с помощью характеристического уравнения и собственных значений. Для квадратной матрицы A существует диагональная матрица D и обратимая матрица P, такие, что A = PDP^(-1), где D – диагональная матрица, а столбцы матрицы P являются собственными векторами матрицы A.
Какие практические задачи решаются после приведения матрицы к диагональному виду?
После приведения матрицы к диагональному виду можно решить ряд практических задач, включая вычисление степеней матрицы, решение линейных систем уравнений, нахождение обратной матрицы, решение дифференциальных уравнений и другие задачи линейной алгебры и математической физики. Диагональные матрицы упрощают работу с матричными уравнениями и позволяют наглядно представить структуру матрицы.
Почему диагональные матрицы являются удобными для анализа и вычислений?
Диагональные матрицы удобны для анализа и вычислений, потому что в них все элементы вне главной диагонали равны нулю. Это означает, что перемножение диагональных матриц сводится к поэлементному умножению диагональных элементов, что делает процесс умножения более простым. Также диагональные матрицы позволяют легко возводить в степень и находить обратную матрицу, что значительно упрощает решение многих задач, связанных с линейной алгеброй и математической физикой.



